Электрохимия. Вопросы коллоквиума к разделу Электрохимия Основные положения теории электролитической диссоциации
 Скачать 6.64 Mb. Скачать 6.64 Mb.
|
|
Электрическая проводимость растворов электролитов. Удельная и молярная электрические проводимости. Она обусловлена наличием носителей заряда катионов и анионов. Как и для любой системы, включающей проводник электрического тока ,величиной является характеристика R- сопротивление системы. 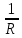 - электрическая проводимость системы. - электрическая проводимость системы.Между характеристикой l-длины проводника, величиной его сечения (S) и R существует зависимость : 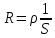 Где ρ- удельное сопротивление [Ом*см] ᴂ= 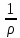 [ [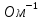 * *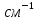 ] ]ᴂ= 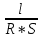 = =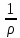 ; ; 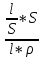 = =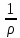 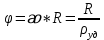 ᴂ-удельная электропроводность- проводимость электрического тока в растворе сильного электролита в постоянном электрическом токе, находящегося между электродами с поверхностью S=1 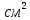 и расстоянии между ними l= 1см и расстоянии между ними l= 1смСуществует другая характеристика электрической проводимости сильных электролитов. ʎ- молярная или эквивалентная электропроводность 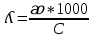 [ [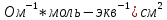 ] ]где С- молярная концентрация [ 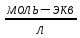 ] ]1000-коэффициент, учитывающий переход от 1л к 1 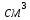 . ʎ относится к раствору, содержащему . ʎ относится к раствору, содержащему 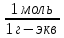 растворенного электролита помещенному между электродами на расстоянии 1 см. растворенного электролита помещенному между электродами на расстоянии 1 см.- Ионы раствора электролита при наличии постоянной разности потенциалов перемещаются в электрическом поле и обладают определенной подвижностью. u-подвижность ионов В общем случае подвижность ионов определяется : 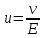 v- скорость движения ионов Е- напряженность электрического поля Между характеристиками подвижности и электрической проводимости существует взаимосвязь: 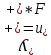 } }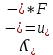 F-число Фарадея Для характеристики ʎ раствора слабого электролита можно записать, что 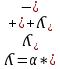 Где α- степень диссоциации В случае разбавления α растет и стремится к α=1. При бесконечном разбавлении α=1 и 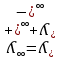 - закон Кольрауша - закон Кольрауша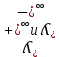 - эквивалентные (молярные) электропроводности растворов электролита для катиона и аниона. - эквивалентные (молярные) электропроводности растворов электролита для катиона и аниона.Они есть в справочных данных Для слабых электролитов можно считать: α= 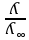 Зависимость электрической проводимости растворов слабых и сильных электролитов от концентрации электролита. В растворах электролитов концентрация влияет на величину электр.проводимости. Для характеристики ʎ: с увеличением разбавления ʎ растет и при С→0 ʎ→ 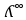 Для растворов сильных и слабых электролитов: 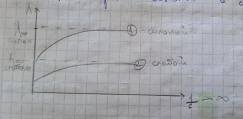 Для ᴂ=f(c) зависимость имеет сложный характер ʎс=f(ᴂ) 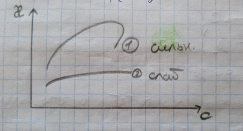 Для сильных электролитов известен закон Кольрауша или закон квадратного корня: ʎ= 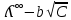 где b- постоянная, С- концентрация Для слабых электролитов: 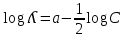 Электрическая проводимость зависит от температуры. При увеличении температуры на 1 градус эта характеристика возрастает на 2 %. Влияют свойства самой среды. Находят выражение в диэлектрической проницаемости; размеры ионов. Электрофоретическое и релаксационное торможение в растворах сильных электролитов. Для сильных электролитов проявляется 2 типа эффектов, которые приводят к понижению электр. проводимости: 1)Электрофоретический эффект Его сущность заключается в том, что центральный ион и ионная атмосфера в постоянном электрическом поле перемещается навстречу друг другу. Это равносильно перемещению потока жидкости навстречу движущимся ионам. Это приводит к уменьшению электропроводности ʎ на характеристику 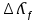 2) Релаксационный эффект Связан с ионной атмосферой вокруг центрального иона, при его перемещении ионная атмосфера разрушается. При этом создается новая атмосфера в следующий промежуток времени и т.д. В итоге это сопровождается тем, что суммарный заряд ионной атмосферы будет больше, чем центрального иона. Это приводит к тормозящему эффекту и ʎ↓ на 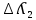 В итоге ʎ= 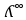 - -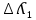 - -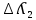 за счет этих эффектов. При за счет этих эффектов. При 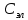 →0, →0, 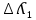 и и 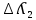 тоже →0, то следует ʎ≈ тоже →0, то следует ʎ≈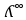 Подвижность ионов и числа переноса. В растворе электролита ионы движутся беспорядочно. При наложении на раствор электрического поля беспорядочное движение ионов в основном сохраняется, но одно из направлений становится преимущественным. Направленность движения ионов можно создать при помощи электродов, опущенных в раствор. Чем выше градиент потенциала, т.е. чем больше падение напряжения на 1 см раствора электролита вдоль направления электрического поля, тем выше скорость движения иона в электрическом поле Самыми высокими скоростями обладают ионы Н3О⁺ и ОН⁻ Н3О⁺ + Н2О Н2О + ОН⁻ Причем средняя продолжительность существования иона Н3О⁺ =10⁻¹¹ сек. Переносчиками тока в растворах электролитов служат ионы, но так как абсолютные скорости движения анионов и катионов в данном растворе неодинаковы, то большую долю тока всегда переносят более быстрые ионы. Величину, при помощи которой можно выразить долю электричества, переносимую ионами данного вида, называют числом переноса; для катионов оно обозначается t+ и для анионов через t-. Количество электричества, перенесенное ионами i-того вида через данное сечение раствора электролита, определяется по уравнению qi = zi*F*Ci*vi*S*t, где zi_-валентность, Сi- концентрация, vi- абсолютная скорость ионов i -того вида, S - площадь сечения, t- время. Число переноса ti определяется соотношением: ti = где q - количество электричества, перенесенное всеми ионами. В частности, для раствора сильного электролита можно записать t+ = 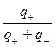 , ,t- = 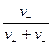 . .Подставив предыдущие выражения, получим t+ = t- = при этом t⁺ + t⁻ = 1. Различие в скоростях движения анионов и катионов приводит к тому, что они переносят разные количества электричества, но это не влечет за собой нарушение электронейтральности раствора, а лишь изменяет концентрацию электролита у катода и анода. Между числами переноса и подвижностями ионов в растворе сильных электролитов существует зависимость: из уравнений λ⁺ = F*v⁺ и λ- = F*v⁻ следует (в уч. Стр. 237) t+ = 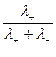 , ,t- = λ+ = ʌ*t+ ; λ- = ʌ*t-. (ʌ-молярная электрическая проводимость (См*см²*моль⁻¹), λ⁺ и λ⁻-подвижности ионов (См*м²*моль⁻¹), t⁺ и t⁻ - числа переноса ионов). Числа переноса остаются практически постоянными до тех пор, пока концентрация сильного электролита не превышает 0,2 г-экв/л, при дальнейшем увеличении концентрации наблюдается их изменение. С ростом температуры абсолютные скорости ионов и подвижности ионов увеличиваются, но не в одинаковой мере. Поэтому числа переноса с изменение температуры также меняются. При этом если число переноса катиона увеличивается, то числа переноса анионов уменьшаются и наоборот. Скачки потенциалов на границах фаз. Двойной электрический слой. Рассмотрим систему из двух разнородных фаз. При их соприкосновении система приходит в неравновесное состояние. Согласно второму закону термодинамики система будет стремиться к равновесию. В результате возникает процесс, который сопровождается обменом заряженных частиц между фазами. Такой процесс приводит к тому, что по одну сторону от границы раздела появляется избыток заряда определенного знака, а по другую – его недостаток. Возникает двойной электрический слой (ДЭС). Он напоминает плоский конденсатор с заряженными обкладками. Значит, на границе раздела фаз электрический потенциал φ резко изменяется и наблюдается скачок потенциала ∆φ. В общем случае могут иметь место следующие скачки потенциалов: 1. поверхностные потенциалы, возникающие на границе раздела вакуум-металл; 2. контактные потенциалы, возникающие на границе раздела двух разных металлов, то есть металл-металл; 3. электродные потенциалы, которые возникают на границе раздела металл – раствор его соли; 4. диффузионный потенциал, возникающий на границе раздела двух разных растворов электролита. Контактный потенциалвозникает на поверхности соприкосновения двух металлов. Он обусловлен разной концентрацией электронов проводимости в рассматриваемых фазах, определяется разностью работ выхода электрона, зависит от температуры и для некоторых пар металлов может достигать нескольких вольт. Абсолютную величину контактного потенциала определить невозможно. Поэтому используют его относительные значения, например контактный потенциал, относительно золота. Диффузионный потенциал возникает на поверхности раздела двух растворов электролитов с одинаковым растворителем, но отличающиеся по виду электролита или по его концентрации. Такой потенциал возникает за счет различия абсолютных скоростей (подвижностей) ионов электролита. Например, в растворах нитрата серебра AgNO3 подвижность аниона NO3- выше, чем катиона Ag+. Диффузия растворенного вещества происходит в направлении убывания его концентрации. Вследствие этого граница раздела двух растворов AgNO3 заряжается отрицательно со стороны более разбавленного раствора и положительно со стороны раствора с большей концентрацией электролита. Возникает диффузионный ДЭС. По истечении определенного времени, скорости диффузии катионов Ag+ и анионов NO3- выравниваются. На границе раздела возникает равновесие, при котором ток отсутствует, а электролит диффундирует как единое целое в виде AgNO3. Установившуюся между растворами разность потенциалов называют равновесным диффузионным потенциалом φд. Измерить его абсолютное значение невозможно. На практике используют относительное значение. Так как трудно учесть абсолютное значение диффузионного потенциала, то его стремятся максимально уменьшить. Для этого растворы электролитов разъединяют в пространстве и между ними помещают солевой мостик. Солевой мостик – это U-образная стеклянная трубка, внутри её находится раствор электролита, у которого подвижности ионов одинаковы, например, NaCl, NH4NO3. Электрическая проводимость на границах контакта растворов с солевым мостиком обеспечивается этими ионами, при этом возникают очень малые обратные по знаку диффузионные потенциалы, суммой которых пренебрегают. Электродный потенциал φM/L возникает на границе металл – раствор электролита. При погружении металлической пластинники, с удаленной оксидной пленкой, в растворе электролита между металлом и раствором возникает ДЭС и скачок потенциала, называемый электродным потенциалом. Основная причина его возникновения – это движение ионов между поверхностью металла и раствором. Следует отметить для этих явлений важную роль специфической адсорбции ионов и полярных молекул, а также выход электронного газа за границы кристаллической решетки металла. Рассмотрим образование ДЭС при погружении металлической пластинки в воду или другой полярный растворитель. В этом случае происходят следующие процессы. 1. Катионы, расположенные в узлах кристаллической решетки металла, взаимодействуют на поверхности с полярными молекулами воды, которые ориентированы к катионам своими отрицательными полюсами. При сильном взаимодействии катионы отрываются от поверхности металла и переходят в жидкую фазу М(т) → Мz+ (р) +Ze- (1). Системой поглощается энергия, равная энергия связи катиона с кристаллической решеткой ЕМZ+. Образующийся избыток электронов заряжает поверхность металла отрицательно, а выходящие катионы заряжают граничащий с металлом слой воды положительно. 2. Катионы металла гидратируются полярными молекулами воды в объёме жидкой фазы MZ+ (p) +nH2O → MZ+∙ nH2O (p) (2). Системой выделяется энергия, равная энергии гидратации Ег. В соответствии с термодинамической системой знаков ЕМZ+ > 0 и Ег < 0 (3). Вышерассмотренные процессы 1 и 2 могут протекать одновременно (параллельно друг другу). В этом случае их описывают уравнением М(т) + nH2O → MZ+∙ nH2O (p) + Ze- (4). 3. Концентрирование гидратированных катионов в граничном с поверхностью металла слое жидкости для компенсирования избыточного поверхностного заряда посредством электростатического взаимодействия. Таким образом, на границе металл – вода возникает обменный ДЭС и соответствующий ему скачок потенциала – электродный потенциал φM/L. С ростом данного потенциала φM/L все быстрее протекают обратные процессы, в результате которых происходит дегидратация ионов металла и их восстановление до атомов в соответствии с уравнением MZ+∙ nH2O (p) + Ze- → М(т) + nH2O. При определенном скачке потенциала возникает равновесие, описываемое уравнением М(т) + nH2O ↔ MZ+∙ nH2O (p) + Ze- (5). Данному равновесию отвечает равенство скоростей прямого и обратного процессов. В упрощенной форме ему соответствует выражение, в котором нет молекул воды. Такая форма записи рекомендована ИЮПАК и называется уравнением электродного процесса MZ+ (p) + Ze- ↔ М(т) (6). Электродный процесс, представленный в такой форме иногда называют потенциалопределяющим процессом. При погружении металла в раствор его соли, который является электролитом, происходят сходные явления, но равновесие наступает при другом скачке потенциала. Для таких процессов характерно то, что φM/L = φMZ+/M (7). Равновесным электродным потенциалом φM/L = φMZ+/M называют скачок потенциала, установившийся между металлом и раствором электролита в условиях равновесия. Металл в растворе собственной соли может заряжаться как отрицательно (Al, Zn, Fe, Ni), так и положительно (Cu, Ag, Au). 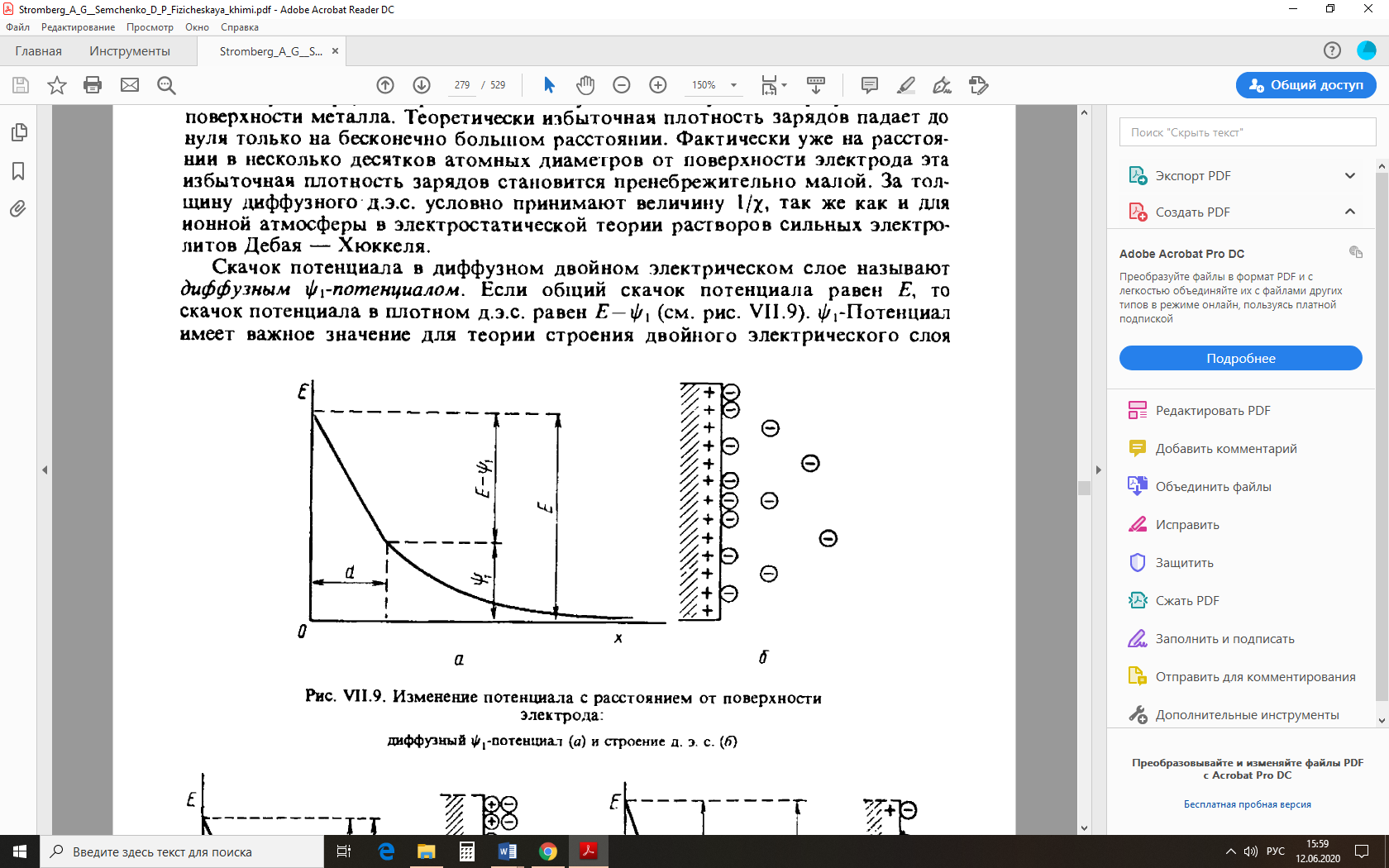 ЭДС гальванического элемента. Вывод уравнения Нернста. Рассмотрим простейший гальванический элемент Даниэля – Якоби, состоящий из двух полуэлементов – цинковой и медной пластин, помещенных в растворы сульфатов цинка и меди соответственно, которые соединены между собой посредством электролитического ключа – например, полоски бумаги, смоченной раствором какого-либо электролита. Схематически данный элемент изображается следующим образом: Zn / Zn2+ // Cu2+ / Cu На поверхности каждого из электродов имеет место динамическое равновесие перехода ионов металла из электрода в раствор и обратно, характеризуемое потенциалом ДЭС (зарядом на электроде q). Если соединить медный и цинковый электроды металлическим проводником, немедленно произойдет перераспределение зарядов – электроны начнут перемещаться с электрода с более отрицательным зарядом (в нашем случае – цинкового) на электрод с более положительным зарядом (медный), т.е. в проводнике возникнет электрический ток. Изменение величины заряда каждого из электродов нарушает равновесие – на цинковом электроде начнется процесс перехода ионов из электрода в раствор (окисление металла), на медном – из раствора в электрод (восстановление металла); при этом протекание процесса на одном электроде обусловливает одновременное протекание противоположного процесса на другом: ZnО ––> Zn2+ + 2е- Сu2+ + 2е- ––> СuО Электрод, на котором при работе гальванического элемента протекает процесс окисления, называется анодом, электрод, на котором идет процесс восстановления – катодом. При схематическом изображении гальванических элементов слева записывают анод, справа – катод (стандартный водородный электрод всегда записывают слева). Суммарный окислительно-восстановительный процесс, происходящий в гальваническом элементе, выражается следующим уравнением: Сu2+ + Zno ––> Сuo + Zn2+ Т.о., гальванический элемент можно определить как прибор для преобразования химической энергии окислительно-восстановительной реакции в электрическую за счет пространственного разделения процессов окисления и восстановления. Работа, которую может совершить электрический ток, вырабатываемый гальваническим элементом, определяется разностью электрических потенциалов между электродами (называемой обычно просто разностью потенциалов) ΔΦ и количеством прошедшего по цепи электричества q: Работа тока гальванического элемента (и, следовательно, разность потенциалов), будет максимальна при его обратимой работе, когда процессы на электродах протекают бесконечно медленно и сила тока в цепи бесконечно мала. Максимальная разность потенциалов, возникающая при обратимой работе гальванического элемента, есть электродвижущая сила (ЭДС) гальванического элемента. ДС гальванического элемента E удобно представлять в виде разности некоторых величин, характеризующих каждый из электродов – электродных потенциалов; однако для точного определения этих величин необходима точка отсчета – точно известный электродный потенциал какого-либо электрода. Электродным потенциалом электрода εэ называется ЭДС элемента, составленного из данного электрода и стандартного водородного электрода , электродный потенциал которого принят равным нулю. При этом знак электродного потенциала считают положительным, если в таком гальваническом элементе испытуемый электрод является катодом, и отрицательным, если испытуемый электрод является анодом. Необходимо отметить, что иногда электродный потенциал определяют как "разность потенциалов на границе электрод – раствор", т.е. считают его тождественным потенциалу ДЭС, что не вполне правильно (хотя эти величины взаимосвязаны). Величина электродного потенциала металлического электрода зависит от температуры и активности (концентрации) иона металла в растворе, в который опущен электрод; математически эта зависимость выражается уравнением Нернста (здесь F – постоянная Фарадея, z – заряд иона): В уравнении Нернста ε° – стандартный электродный потенциал, равный потенциалу электрода при активности иона металла, равной 1 моль/л. Стандартные электродные потенциалы электродов в водных растворах составляют ряд напряжений. Величина ε° есть мера способности окисленной формы элемента или иона принимать электроны, т.е. восстанавливаться. Иногда различием между концентрацией и активностью иона в растворе пренебрегают, и в уравнении Нернста под знаком логарифма фигурирует концентрация ионов в растворе. Величина электродного потенциала определяет направление процесса, протекающего на электроде при работе гальванического элемента. На полуэлементе, электродный потенциал которого имеет большее (иногда говорят – более положительное) значение, будет протекать процесс восстановления, т.е. данный электрод будет являться катодом. Рассмотрим расчёт ЭДС элемента Даниэля – Якоби с помощью уравнения Нернста. ЭДС всегда является положительной величиной и равна разности электродных потенциалов катода и анода: Как видно из уравнения (5), ЭДС элемента Даниэля – Якоби зависит от концентрации (точнее говоря, активности) ионов меди и цинка; при их равных концентрациях ЭДС элемента будет равна разности стандартных электродных потенциалов: Анализируя уравнение (5), можно определить предел необратимой работы гальванического элемента. Поскольку на аноде идет процесс окисления цинка, концентрация ионов цинка при необратимой работе гальванического элемента постоянно увеличивается; концентрация ионов меди, напротив, уменьшается. Отношение концентраций ионов меди и цинка постоянно уменьшается и логарифм этого отношения при [Сu2+] < [Zn2+] становится отрицательным. Т.о., разность потенциалов при необратимой работе гальванического элемента непрерывно уменьшается; при E = 0 (т.е. εк = εа) гальванический элемент не может совершать работу (необратимая работа гальванического элемента может прекратиться также и в результате полного растворения цинкового анода).  |
