Расписанные билеты к экзамену по информатке 2 семестр. Экзамен по информатике. Вопросы текущего контроля дисциплины Информационные технологии (2022)

• Название: Вопросы текущего контроля дисциплины Информационные технологии (2022)
• Анкор: Расписанные билеты к экзамену по информатке 2 семестр
• Дата: 06.11.2022
• Размер: 3.14 Mb.
• Имя файла: Экзамен по информатике.docx
• Тип: Документы; #773076
• страница: 1 из 4

Вопросы текущего контроля дисциплины «Информационные технологии» (2022)

1. Классификация информационных систем

В широком смысле ИС - есть совокупность технического, программного и организационного обеспечения, а также персонала, предназначенная для того, чтобы своевременно обеспечивать надлежащих людей надлежащей информацией.

В узком смысле ИС - программно-аппаратная система, предназначенная для автоматизации целенаправленной деятельности конечных пользователей, обеспечивающая, в соответствии с заложенной в нее логикой обработки, возможность получения, модификации и хранения информации.

По степени распределённости отличают: настольные, или локальные ИС, в которых все компоненты (БД, СУБД, клиентские приложения) находятся на одном компьютере; распределённые ИС, в которых компоненты распределены по нескольким компьютерам.

Клиент-серверные ИС: В двухзвенных ИС всего два типа «звеньев»: сервер баз данных, на котором находятся БД и СУБД, и рабочие станции, на которых находятся клиентские приложения.

В многозвенных ИС добавляются промежуточные «звенья»: серверы приложений; пользовательские клиентские приложения взаимодействуют с промежуточными звеньями, а не обращаются к СУБД напрямую.

По степени автоматизации: автоматизированные: информационные системы, в которых автоматизация может быть неполной (нужно вмешательство персонала)

автоматические: информационные системы, в которых автоматизация является полной, то есть вмешательство персонала не требуется или требуется только эпизодически. «Ручные ИС» («без компьютера») существовать не могут, поскольку обязательно наличие в составе ИС аппаратно-программных средств.

По характеру обработки данных: информационно-справочные ИС, в которых нет сложных алгоритмов обработки данных, а целью системы является поиск и выдача информации в удобном виде; ИС обработки данных, в которых данные подвергаются обработке по сложным алгоритмам.

По сфере применения: экономическая ИС— ИС, предназначенная для выполнения функций управления на предприятии; медицинская ИС —ИС, предназначенная для использования в мед. Учреждениях; географическая ИС — ИС, обеспечивающая сбор, хранение, обработку, доступ, отображение и распространение пространственных данных.

По масштабности: Персональная ИС предназначена для решения задач одного человека; Групповая ИС ориентирована на коллективное использование информации членами рабочей группы; Корпоративная ИС охватывает информационные процессы предприятия, достигая их полной согласованности и прозрачности.

2. Отличительные особенности знаний по сравнению с данными

Знания отличаются от сведений концептуальной направленностью, пониманием роли сведений в окружающей действительности данные можно определить как информацию, фиксированную в определенной форме, пригодной для последующей обработки, хранения и передачи. В системах обработки информации под знаниями понимают сложноорганизованные данные, содержащие одновременно как фактографическую (т.е. регистрация некоторого факта), так и семантическую (т.е. смысловое описание зарегистрированного факта) информацию, которая может потребоваться пользователю.
Отличие знаний от данных: интерпретируемость, наличие классифицирующих отношений, наличие ситуативных связей. Переход от данных к знаниям — логическое следствие развития и усложнения информационных структур, обрабатываемых на ЭВМ.

3. Особенности знаковой (семиотической) системы

Синтаксис описывает внутреннее устройство знаковой системы, т. е. правила построения и преобразования сложных знаковых выражений (для естественного языка, как известно, синтаксис определяет правильное построение предложений и связного текста)
Семантика определяет отношения между знаками и их свойствами, т.е. задает смысл или значения конкретных знаков
Прагматика определяет знак с точки зрения конкретной сферы его применения либо субъекта, использующего данную знаковую систему

4. Система представления знаний и ее структура

В системах обработки информации под знаниями понимают сложноорганизованные данные, содержащие одновременно как фактографическую (т.е. регистрация некоторого факта), так и семантическую (т.е. смысловое описание зарегистрированного факта) информацию, которая может потребоваться пользователю

—сложноорганизованные данные могут иметь в своем составе встроенные процедуры обработки, которые активизируются в процессе работы с данными (фактографические же данные играют в процессе обработки пассивную роль)

Бз- база знаний, бд- база данных, Ибд- информационная база данных



5. Архитектура банка знаний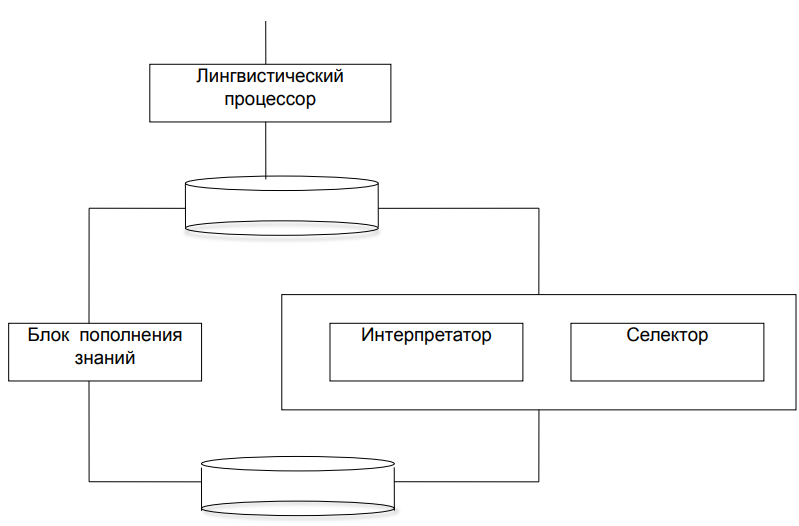



6. Принципы построения формальных теорий моделей знаний

Моделирование является эффективным способом человеческого познания. оно основано на замене одного объекта (оригинала) другим объектом (моделью) с целью изучения

—классификация позволяет систематизировать объекты, облегчает их изучение, упорядочивает терминологию и может привести к важным научным обобщениям

Естественный язык: достоинства (и они же недостатки): неполнота, избыточность, неоднозначность.

Нужно, чтобы любой терминальный символ языка интерпретировался однозначно.

Необходимы языки, которые удовлетворяют следующим требованиям:

- однозначность каждого слова

- эксплицитность (абсолютная явность)

- последовательность (то есть невозможность использовать то, что не было определено ранее).

Такой язык является формальным, а при достаточном формализме – математическим.

7. Семантические сети для представления знаний

Пусть заданы конечные множества символов А={A1 , …, Ar }, называемые атрибутами, и конечное множество R={R1 , …, Rm} отношений. Схемой или интенсионалом отношения Ri называют набор пар: INT(Ri ) = {…,[Aj , DOM(Aj )] ,…}, где Ri – имя отношения, DOM(Aj ) – домен Aj , т.е. множество значений атрибута Aj отношения Ri.

Экстенсионалом отношения Ri называют множество: EXT(Ri ) = {F1 ,…,Fp }, где Fk (k=1,p) – факт отношения Ri . Факт задаётся совокупностью пар вида “атрибут – значение”, называемых атрибутивными парами. Под фактом понимают конкретизацию определенного отношения между указанными объектами

Граф семантической сети



8. Основные объекты в семантических сетях

Понятия – сведения об абстрактных или физических объектах предметной области. События – это действия, которые могут внести изменения в предметную область. Свойства – используются для уточнения понятий, событий или других свойств.

9. Понятие интенсионала и экстенсионала

Схемой или интенсионалом отношения Ri называют набор пар: INT(Ri ) = {…,[Aj , DOM(Aj )] ,…}, где Ri – имя отношения, DOM(Aj ) – домен Aj , т.е. множество значений атрибута Aj отношения Ri.

Экстенсионалом отношения Ri называют множество: EXT(Ri ) = {F1 ,…,Fp }, где Fk (k=1,p) – факт отношения Ri . Факт задаётся совокупностью пар вида “атрибут – значение”, называемых атрибутивными парами. Под фактом понимают конкретизацию определенного отношения между указанными объектами.

10. Фреймовые модели представления знаний

Фиксирует жесткую структуру информационных единиц, называемых протофреймом { n, (V1 , G1 , P1 ), (V2 , G2 , P2 ),... , (Vk , Gk , Pk )} где n - имя фрейма; Vj - имя слота; Gj - значение слота; Pj – процедура.

Заполняя значения слотов от протофрейма переходим к фрейму экземпляру.

Фреймы соответствуют понятиям, отражающим объекты, явления, характеристики предметной области

Модель представления знаний: ◦ набор фреймов, образующих библиотеку внутреннего представления знаний ◦ механизм их преобразования, связывание и т. д.

Содержит как информационные, так и процедуральные элементы.

Два типа фреймов: профрейм - это интенсиональное описание некоторого множества фреймов-примеров. фрейм-пример - это экстенсиональное описание соответствующего фреймапрототипа < фрейм > ::= [< имя >] < ссылка на прототип > < слот > {< слот >} < слот > ::= < имя слота > < значение > [{< процедура >}].

11. Представление знаний с помощью продукций

(Представление – это действие, делающее некоторое понятие воспринимаемым посредством фигуры, записи, языка или формализма. ОТНОСИТСЯ КО ВСЕМУ ГДЕ ЕСТЬ СЛОВО «ПРЕДСТАВЛЕНИЕ»

Представление знаний – формализация истинных убеждений посредством фигур, записей или языков)

Продукционные модели (использует некоторые элементы логических и сетевых моделей).

Под продукцией понимается выражение: (i); Q; Р; А=>В; N где i – имя продукции, с помощью которого данная продукция выделяется из всего множества продукций; Q – сфера применения продукции; А=>В – ядро продукции; Р – условие применимости ядра.

Классификация ядер ядро: А=>В 1. ЕСЛИ А, ТО ВОЗМОЖНО В; 2. ЕСЛИ А, ТО С ВЕРОЯТНОСТЬЮ р РЕАЛИЗОВАТЬ В; 3. ЕСЛИ А, ТО С БОЛЬШЕЙ ДОЛЕЙ УВЕРЕННОСТИ В; 4. ЕСЛИ А, ТО С ВЕРОЯТНОСТЬЮ р МОЖНО ОЖИДАТЬ В.

12. Понятие формальной грамматики

формальный язык — это математическая модель реального языка. Под реальным языком здесь понимается некий способ коммуникации (общения) субъектов друг с другом.

формальные языки — это просто множества цепочек, составленных из символов некоторого конечного алфавита.

Формальная грамматика или просто грамматика в теории формальных языков — способ описания формального языка, то есть выделения некоторого подмножества из множества всех слов некоторого конечного алфавита.

Теория формальных грамматик: Пусть V - непустое конечное множество символов (элементов), называемых словарем (алфавитом).

Произвольную конечную последовательность символов называют цепочкой в словаре V (цепочки получаются с помощью операции конкатенации - соединения).

Множество всевозможных цепочек в словаре V называют языком.

Различают распознающие, порождающие и преобразующие грамматики.

13. Порождающие грамматики

Порождающие грамматики: G = ( T, N, P, S ) ◦ где T - конечное непустое множество символов, называемых терминальным (основным) словарем; ◦N - конечное непустое множество символов, называемых нетерминальным (вспомогательным) словарем; ◦ P - конечное непустое множество правил вывода (правил переписывания, продукций); ◦ S - начальный символ.

Пример: Пусть грамматика задана следующим образом: T = { a , b } , N = { S , A , B } , S = S , P = { 1. S aB ; 2. S bA ; 3. A aS ; 4. A bAA ; 5. A a ; 6. B bS ; 7. B  aBB ; 8. B  b }. Типичные выводы предложений : 1) S  aB  ab 2) S  aB  abS  abbA  abba 3) S  bA  ba 4) S  bA  bbAA  bbaA  bbaa

14. Классификация формальных грамматик

тип 0 - это грамматики, в которых не накладывается никаких ограничений на правила вывода    , где  и  могут быть любыми цепочками из V
типа 1 - это грамматики, в которых содержатся правила    , удовлетворяющие условиям   А  ,     , где А - нетерминальный символ, а , , 1 , 2 ,  - цепочки из V.
тип 2 - это грамматики, в которых допустимы лишь правила вида А   , где А  N , а  - любая непустая цепочка из V .
тип 3 имеют правила вида A  aB либо A  b, где A,B  N ; а b  T. Заметим, что A,B,a,b являются одиночными символами (не цепочками) соответствующих словарей.
Неукорачивающие грамматики - это грамматики, в которых для любого правила    справедливо соотношение    
Грамматика непосредственносоставляющих имеет правила вида    или А  , где A  N; , ,  - произвольные цепочки
Грамматики, использующие правила перехода от одних выражений к другим, несущим ту же информацию, называются трансформационными.
Трансформационная грамматика: Первая компонента - НС – грамматика.
Вторая (Т – компонента) образована правилами трансформации p1 ,...pn  l, где n1, а p1 ,...pn ,l - не цепочки символов, а С – маркеры
Таким образом, вывод в трансформационной грамматике есть отображение набора С - маркеров в новый С – маркер, представляющий поверхностную структуру предложения.

15. Виды компьютерной графики

Под компьютерной графикой понимается комплекс программных и аппаратных технологий ПК, применяемых для создания, видоизменения и отображения неподвижных изображений, записанных в цифровом виде (служит базой для отображения как текста, так и анимации и движущихся изображений)
Виды компьютерной графики: растровая, векторная и фрактальная; трехмерная (3D); графика черно-белая и цветная; графика компьютерной анимации и видеомонтажа; инженерная графика; веб-графика; компьютерная полиграфия

16. Растровые изображение и их характеристики

Растровые изображения делятся на элементы (pixels), количество которых по вертикали и горизонтали определяет размер картинки.
Важными характеристиками изображения являются:1) Размер изображения в пикселях — может выражаться в виде количества пикселей по ширине и по высоте (800 × 600 px и т. д.) или же в виде общего количества пикселей 2)Количество используемых цветов или глубина цвета (эти характеристики имеют следующую зависимость: N=2^k N — количество цветов, k — глубина цвета); 3) Цветовое пространство (цветовая модель) — RGB, CMYK и др.; 4) Разрешение изображения — величина, определяющая количество точек (элементов растрового изображения) на единицу площади (или единицу длины).
Растровую графику редактируют с помощью растровых графических редакторов. Создаётся растровая графика фотоаппаратами, сканерами, непосредственно в растровом редакторе, а также путём экспорта из векторного редактора или в виде снимков экрана.

17. Понятие линиатуры растра и ее связь с разрешением изображения

Размер точки растрового изображения на твердой копии (бумаге, пленке и т. д.) зависит от примененного метода и параметров растрирования оригинала. При растрировании на оригинал как бы накладывается сетка линий, ячейки которой образуют элемент растра. Частота сетки растра измеряется числом линий на дюйм (lines per inch — lpi) и называется линиатурой.

Связь между линиатурой и разрешением изображения: Устанавливая разрешение для сканирования изображения, всегда следует учитывать линиатуру, с которой будет воспроизводиться иллюстрация в печати. В общем случае считается, что величина разрешения изображения должна не менее чем в 1,4 раза превышать значение линиатуры растра. При воспроизведении изображений с большим числом тонких деталей этот коэффициент должен быть увеличен до 1,7 или даже до 2. Дальнейшее увеличение разрешения не увеличивает качества выходного изображения и обычно ведет лишь к повышению объема файлов.

18. Интенсивность тона и ее связь с разрешением оригинала и частотой растра

19. Динамический диапазон изображения

Динамический диапазон в фотографии описывает соотношение между максимальной и минимальной измеримой интенсивностью света (белым и чёрным, соответственно). В природе не существует абсолютно белого или чёрного — только различные степени интенсивности источника света и отражательной способности предмета.
Оптическая плотность D
D = lg(1/)
D = lg(1/)
 = F /F0 – коэфф.отражения
 = F /F0 – коэфф.пропускания
F0 – падающий световой поток
F – отраженный световой поток
F – пропущенный световой поток
1) Для оптических сред, пропускающих свет, значение D (от 0 до 4)
2) Для поверхностей, отражающих свет, значение D (0 до 2)

20. Характеристики цвета – физические, визуальные, компьютерные

Физические характеристики: мощность, яркость, освещенность
Визуальные параметры: светлота, насыщенность, градация

Компьютерная графика: глубина цвета, цветовая температура

21. Законы Грассмана о цветовом пространстве



22. Цветовая модель RGB и ее особенности

RGB модель построена на основе строения глаза. Она идеально удобна для светящихся поверхностей (мониторы, телевизоры, цветные лампы и т.п.)
Первичные цвета: red, green, blue
по стандарту HDTV
Нельзя представить все видимые цвета как комбинацию R, G и B
Описывает любые цвета монитора набором трех чисел (r,g,b)
в растровом файле набор сохраняется для каждой точки
RGB (аббревиатура английских слов red, green, blue — красный, зелёный, синий) или КЗС — аддитивная(наложение цветов) цветовая модель, описывающая способ кодирования цвета для цветовоспроизведения с помощью трёх цветов, которые принято называть основными. Выбор основных цветов обусловлен особенностями физиологии восприятия цвета сетчаткой человеческого глаза.

23. Цветовая модель CMYK и ее особенности

Cyan (голубой) = белый – красный = зеленый + синий
Magenta (пурпурный) = белый – зеленый = красный + синий
Yellow (желтый) = белый – синий = красный + зеленый
Black (черный)
Дополнительным (complement) называют цвет полученный вычитанием основного из белого ◦ C = G+B = W-R ◦ M = R+B = W-G ◦ Y = R+G = W-B
Субтрактивные основные цвета cyan, magenta, yellow получаются смешением красок (ink/paint)
Используется исключительно для печати.
Подготовка макета в цветовой модели CMYK позволяет добиться максимальной точности изображения и его соответствия первоначальной графике. Работа по созданию картинки в данной цветовой схеме имитирует возможности печатного оборудования непосредственно на мониторе.
Цветоделение в CMYK: 1) не существует красителей точно соответствующих CMY
2) комбинация трех красок не дает черного цвета
3) используемые основные цвета (process colours) – cyan, magenta, yellow и black
4) область охвата CMYK отличается от области охвата RGB

24. Цветовая модель HSB, HSL, HSV и ее особенности

1) соответствует восприятию цвета ◦ Hue (цветовой тон, длина волны) ◦ Saturation (насыщенность) ◦ Value (яркость), Brightness, Lightness

2) модель HSV отображается трехмерной фигурой: H - угол, S - расстояние до оси, V - положение на оси

3) является основой для инструмента colour picker (выбор цвета)

Цветовая модель, в которой координатами цвета являются:

Шкала оттенков — Hue

• Hue — цветовой тон, (например, красный, зелёный или сине-голубой). Варьируется в пределах 0—360°, однако иногда приводится к диапазону 0—100 или 0—1.

• Saturation — насыщенность. Варьируется в пределах 0—100 или 0—1. Чем больше этот параметр, тем «чище» цвет, поэтому этот параметр иногда называют чистотой цвета. А чем ближе этот параметр к нулю, тем ближе цвет к нейтральному серому.

• Value (значение цвета) или Brightness — яркость. Также задаётся в пределах 0—100 или 0—1.

HSL, HLS или HSI (от англ. hue, saturation, lightness (intensity)) — цветовая модель, в которой цветовыми координатами являются тон, насыщенность и светлота. Следует отметить, что HSV и HSL — две разные цветовые модели (lightness — светлота, что отличается от яркости).

25. Цветовая модель XYZ и ее особенности

CIE XYZ — линейная 3-компонентная цветовая модель основных цветов RGB, получена на результатах измерения характеристик человеческого глаза.

Трёхкомпонентная теория XYZ была открыта на основе исследований и сравнений результатов зрительных возможностей «стандартного наблюдателя», то есть гипотетического зрителя, возможности которого были тщательно изучены и зафиксированы в ходе длительных исследований человеческого зрения, проведённых комитетом на больших группах людей.

Функции соответствия цветов — это значения каждой первичной составляющей света — красной, зелёной и синей, которые должны присутствовать, чтобы человек (и животный мир) со средним зрением мог воспринимать все цвета видимого спектра. Этим трём первичным составляющим были поставлены в соответствие координаты X, Y, Z.

Основное свойство, присущее этой системе — положительная определённость — любой физически существующий (ощутимый человеком) цвет представляется в системе XYZ только положительными величинами. С другой стороны, не всем точкам в пространстве XYZ соответствуют реальные цвета в силу неортогональности функций соответствия цветов.

Говоря об «эталонных» оттенках, часто говорят только о паре x, y, считая z = 1-x-y.

Говоря о «яркости» цвета (например, для перевода изображения в чёрно-белое), часто имеют в виду величину Y.

Геометрическое место точек цветности монохроматических излучений называется локусом.
26. Цветовая модель CIE Lab и ее особенности



27. Цветовая палитра, индексная палитра, безопасная палитра Веб

Цветовая палитра – это таблица данных, в которой хранится информация о том, каким кодом закодирован тот или иной цвет. Это таблица создается и хранится вместе с графическим файлом.

Самый удобный для компьютера способ кодирования цвета – 24 - разрядный, True Color. В этом режиме на кодирование каждой цветовой составляющей R (красной), G(зеленой), B(синей), отводится по одному байту (8 битов). Яркость каждой составляющей выражается числом от 0 до 255, и любой цвет из 16,5 миллионов компьютер может воспроизвести по трем кодам. В этом случае цветовая палитра не нужна, поскольку в трех байтах и так достаточно информации о цвете конкретного пикселя.

Индексная палитра.

Существенно сложнее обстоит дело, когда изображение имеет только 256 цветов, кодируемых одним байтом. В этом случае каждый цветовой оттенок представлен одним числом, причем это число выражает не цвет пикселя, а индекс цвета (его номер). Сам же цвет разыскивается по этому номеру в сопроводительной цветовой палитре, приложенной к файлу. Такие цветовые палитры еще называют индексными палитрами. Разные изображения могут иметь разные цветовые палитры. Например, в одном изображении зеленый цвет может кодироваться индексом 64, а в другом изображении это индекс может быть отдан розовому цвету. Если воспроизвести изображение с «чужой» цветовой палитрой, то зеленая елка на экране может оказаться розовой.

В тех случаях, когда цвет изображения закодирован двумя байтами (режим High Color), на экране возможно изображение 65 тысяч цветов. Разумеется, это не все возможные цвета, а лишь одна двести пятьдесят шестая доля общего непрерывного спектра красок, доступного в режиме True Color. В таком изображении каждый двухбайтный код тоже выражает какой-то цвет из общего спектра. Но в данном случае нельзя приложить к файлу индексную палитру, в которой было бы 65 тысяч записей, и ее размер составил бы сотни тысяч байтов. Вряд ли есть смысл прикладывать к файлу таблицу, которая может быть по размеру больше самого файла. В этом случае используют понятие фиксированной палитры. Ее не надо прикладывать к файлу, поскольку в любом графическом файле, имеющем шестнадцатиразрядное кодирование цвета, один и тот же код всегда выражает один и тот же цвет.

«Безопасная» палитра.

Этот термин используют в Web-графике. Поскольку скорость передачи данных в Интернете пока оставляет желать лучшего, для оформления Web-страниц не применяют графику, имеющую кодирование цвета выше 8-разрядного.

При этом возникает проблема, связанная с тем, что создатель Web-страницы не имеет ни малейшего понятия о том, на какой модели компьютера и под управлением каких программ будет просматриваться его произведение. Он не уверен, не превратится ли его «зеленая елка» в красную или оранжевую на экранах пользователей.

В связи с этим принято следующее решение. Все наиболее популярные программы для просмотра Web-страниц (браузеры) заранее настроены на некоторую одну фиксированную палитру. Если разработчик Web-страницы при создании иллюстраций будет применять только эту палитру, то он может быть уверен, что пользователи всего мира увидят рисунок правильно.

В этой палитре не 256 цветов, как можно было бы предположить, а лишь 216. Это связано с тем, что в Интернете работают люди с разными компьютерами, а не только с IBM PC, и не все компьютеры могут воспроизводить 256 цветов.

Такая фиксированная палитра, жестко определяющая индексы для кодирования 216 цветов, называется безопасной палитрой.

28. Понятие векторной графики. Математические основы векторной графики

Как в растровой графике основным элементом изображения является точка, так в векторной графике основным элементом изображения является линия (при этом не важно, прямая это линия или кривая).

В векторной графике объем памяти, занимаемый линией, не зависит от размеров линии, поскольку линия представляется в виде формулы, а точнее говоря, в виде нескольких параметров. Что бы мы ни делали с этой линией, меняются только ее параметры, хранящиеся в ячейках памяти. Количество же ячеек остается неизменным для любой линии.

Линия — это элементарный объект векторной графики. Все, что есть в векторной иллюстрации, состоит из линий. Простейшие объекты объединяются в более сложные, например объект четырехугольник можно рассматривать как четыре связанные линии, а объект куб еще более сложен: его можно рассматривать либо как двенадцать связанных линий, либо как шесть связанных четырехугольников. Из-за такого подхода векторную графику часто называют объектно-ориентированной графикой.

Как и все объекты, линии имеют свойства. К этим свойствам относятся: форма линии, ее толщина, цвет, характер линии (сплошная, пунктирная и т. п.). Замкнутые линии имеют свойство заполнения. Внутренняя область замкнутого контура может быть заполнена цветом, текстурой, картой. Простейшая линия, если она не замкнута, имеет две вершины, которые называются узлами. Узлы тоже имеют свойства, от которых зависит, как выглядит вершина линии и как две линии сопрягаются между собой.

Математические основы векторной графики

Точка

Точка на плоскости задается двумя числами (х, у),определяющими ее положение относительно начала координат.

Прямая линия

Из курса алгебры известно, что для задания прямой линии достаточно двух параметров. Обычно график прямой линии описывается уравнением y = kx + b.Зная параметрыkиb,всегда можно нарисовать бесконечную прямую линию в известной системе координат.

Отрезок прямой

Для задания отрезка прямой надо знать еще пару параметров, например координаты х₁и х₂начала и конца отрезка, поэтому для описания отрезка прямой линии необходимы четыре параметра.

Кривая второго порядка

К кривым второго порядка относятся параболы, гиперболы, эллипсы, окружности и другие линии, уравнения которых не содержат степеней выше второй. Прямые линии — это частный случай кривых второго порядка. Отличаются кривые второго порядка тем, что не имеют точек перегиба.Самая общая формула кривой второго порядка может выглядеть, например, так:

x² + a₁y² + a₂xy + a₃x + a₄y + a₅ = 0

Кривая третьего порядка

Отличительная особенность этих более сложных кривых состоит в том, что они могут иметь точку перегиба. Если вы знакомы с графиком функции y=х³, то конечно видели тот перегиб, который происходит в начале координат. Все прямые и кривые второго порядка (например, окружности или эллипсы) являются частными случаями кривых третьего порядка.

В общем случае уравнение кривой третьего порядка можно записать так:

x³ + a₁y³ + a₂x²y + a₃xy² + a₄x² + a₅y² + a₆xy + a₇x + a₈y + a₉ = 0

Видно, что для записи кривой третьего порядка достаточно девяти параметров. Для задания отрезка кривой третьего порядка надо иметь на два параметра больше.

Кривые Безье

Отрезки кривых Безье — это частный случай отрезков кривых третьего порядка. Они описываются не одиннадцатью параметрами, как произвольные отрезки кривых третьего порядка, а лишь восемью, и потому работать с ними удобнее.

Метод построения кривой Безье основан на использовании пары касательных, проведенных к линии в точках ее концов. На практике эти касательные выполняют роль «рычагов», с помощью которых линию изгибают так, как это необходимо. На форму линии влияет не только угол наклона касательной, но и длина ее отрезка. Управление касательной (а вместе с ней и формой линии) производят перетаскиванием маркера с помощью мыши.

29. Понятие кривой Безье. Контуры и их опорные точки. Типы узлов

Кривые Безье — это частный вид кривых третьего порядка, требующий для своего описания меньшего количества параметров (восьми вместо одиннадцати). В основе построения кривых Безье лежит использование двух касательных, проведенных к крайним точкам сегмента линии. На кривизну (форму) линии влияет угол наклона и длина отрезка касательной, значениями которых можно управлять в интерактивном режиме путем перетаскивания их концевых точек. 

Гибкость в построении и редактировании кривых Безье во многом определяется характеристиками узловых точек.