Вопросы Варианты ответов
 Скачать 0.92 Mb. Скачать 0.92 Mb.
|
Область определения функции | 1. 3. 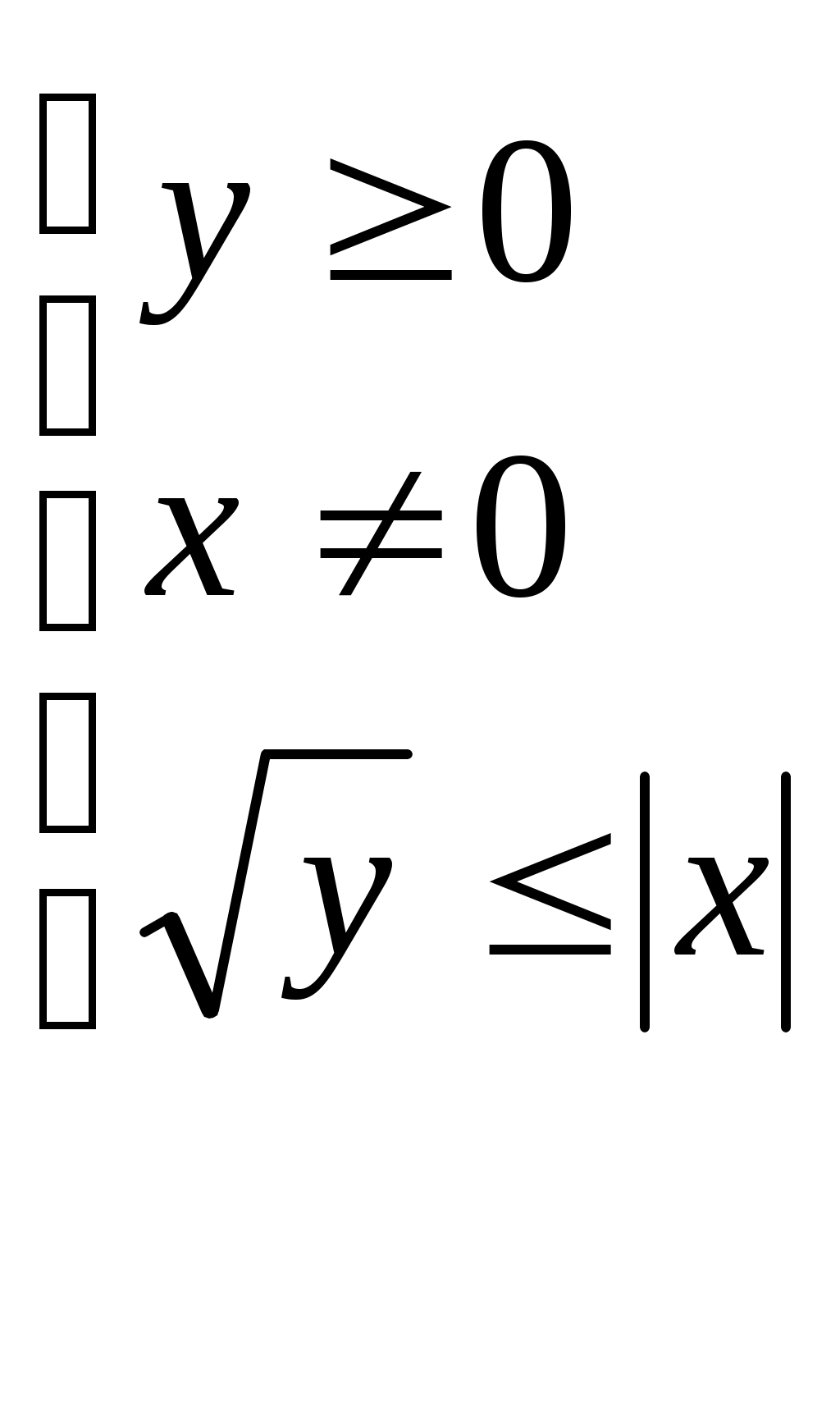 . 4. . 4. | |
| 67 | Линиями уровня | 1. эллипсы. 2. параболы. 3. гиперболы. 4. окружности. |
| 68 | Уравнение касательной плоскости к поверхности | 1. 2. 3. 4. |
| 69 | Областью определения функции | 1. квадрат 2. круг радиуса 2 с центром в начале координат. 3. внутренность круга радиуса 2 с центром в начале координат. 4. вся координатная плоскость |
| 70 | Согласно теореме Вейерштрасса непрерывная функция двух переменных достигает своего наибольшего и наименьшего значения в области, если эта область: | 1. совпадает со всей плоскостью. 2. ограничена и замкнута. 3. ограничена. 4. замкнута. |
| 71 | Функция | 1. имеет минимум в точке (0,0). 2. имеет максимум в точке (0,0). 3. не имеет точек экстремума. 4. имеет максимум в точке (1,1). |
| 72 | Если в стационарной точке М0 функции | 1. нет экстремума. 2. максимум. 3. минимум. 4. нет экстремума или перегиба графика функции. |
| 73 | Для того чтобы в стационарной точке М функция | 1. 2. 3. 4. |
| 74 | Для того чтобы в стационарной точке М функция | 1. 2. 3. 4. |
| 75 | Дифференциал второго порядка | 1. 2. 3. 4. |
| 76 | Уравнение касательной плоскости к поверхности , где | 1. 2. 3. 4. |
| 77 | Указать уравнение касательной к поверхности | 1. 3. |
| 78 | Пусть функция | 1. точка 2. точка 3. точка 4. точка |
| 79 | Точкой максимума функции | 1. (0;0). 2. (1;2). 3. (0;1). 4. (-1;1). |
| 80 | Точка локального экстремума функции | 1. 3. |
| 81 | Для того чтобы стационарная точка М функции | 1. 2. 3. 4. |
| 82 | Для определения параметров | 1. 2. 3. 4. |
| 83 | Для определения параметров | 1. 2. 3. 4. |
| 84 |
