Вопросы Варианты ответов

• Название: Вопросы Варианты ответов
• Дата: 14.01.2022
• Размер: 0.92 Mb.
• Имя файла: FNP.doc
• Тип: Документы; #330980
• страница: 2 из 6

24

Частная производная функции равна

1. 1. 2. -1.

3. -1. 4. .

25

Полная производная вычисляется по формуле

для функции двух переменных с номером

1. ;

2. ;

3. ;

4. ;

26

Производная функции равна

1. .

2. .

3. .

4. .

27

Дифференциал функции равен

1. .

2. .

3. .

4. .

28

Необходимым условием экстремума дифференцируемой функции нескольких переменных является

1. Равенство нулю всех частных производных первого и второго порядка.

2. Равенство нулю всех смешанных производных второго порядка.

3. Равенство нулю всех частных производных второго порядка.

4. Равенство нулю всех частных производных первого порядка.

29

Градиент функции в точке М составляет с касательной к линии уровня этой функции угол, равный:

1. 0. 2. . 3. . 4. .

30

Областью определения функции является

1. внутренность круга радиуса с центром в начале координат.

2. круг радиуса с центром в начале координат.

3. внешность круга радиуса с центром 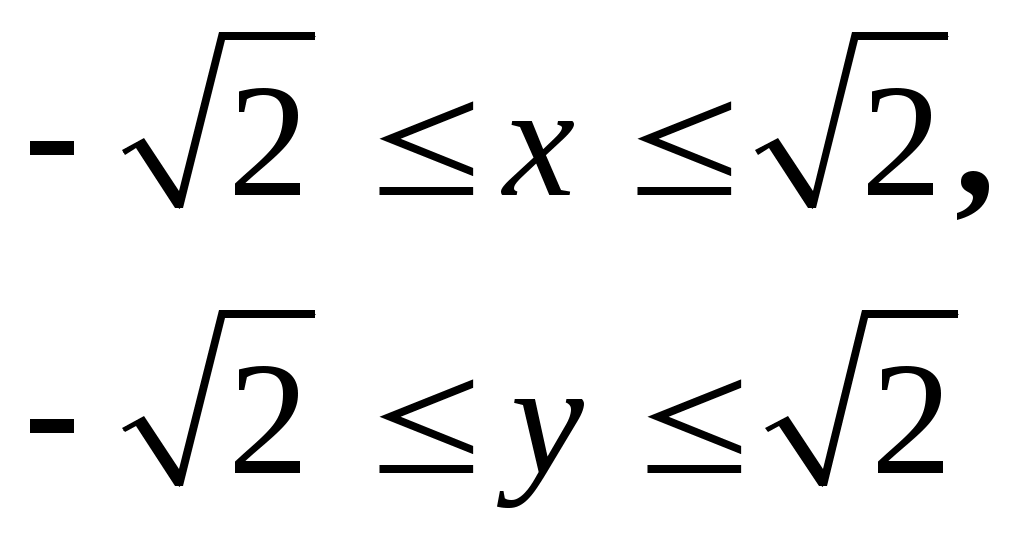в начале координат.

4. квадрат .

31

Полным дифференциалом функции нескольких переменных называется

1. сумма частных производных.

2. главная часть приращения, линейная относительно приращений аргументов.

3. главная часть приращения, нелинейная относительно приращений аргументов.

4. вектор, координатами которого являются частные производные функции.

32

Областью определения функции является

1. .

2. .

3. и .

4. и .

33

_Х

y

1. .

2. .

3. .

4. .

34

Полное приращение функции в точке имеет вид:

1. .

2. .

3. .

4. .

35

Частное приращение функции по переменной точке имеет вид:

1. .

2. .

3 . .

4. .

36

Частная производная – это производная по одной переменной при условии, что остальные переменные

1. полагаются равными нулю.

2. полагаются равными единице.

3. отбрасываются.

4. считаются постоянными.

37

Число А называется пределом функции в точке если

1. .

2. .

3. .

4. .

38

Непрерывна в точке х=0, у=0 функция

1. .

2. .

3. .

4. .

39

Если c=const , то линия уровня для функции двух переменных определяется уравнением

1. .

2. .

3. .

4. .

40

Дифференциал функции равен

1. .

2. .

3. .

4. .

41

Частные производные и функции равны

1. .

2. .

3. .

4. .

42