1. 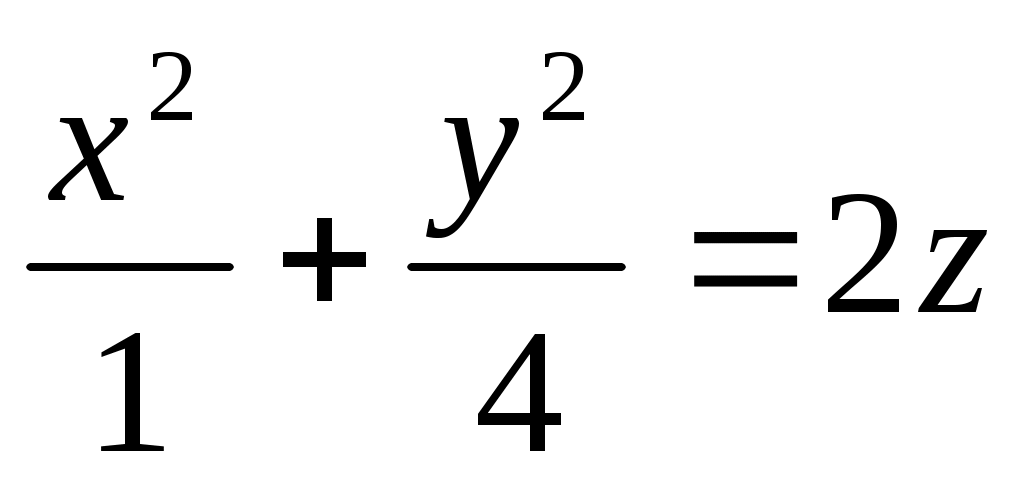 . 2. . 2. 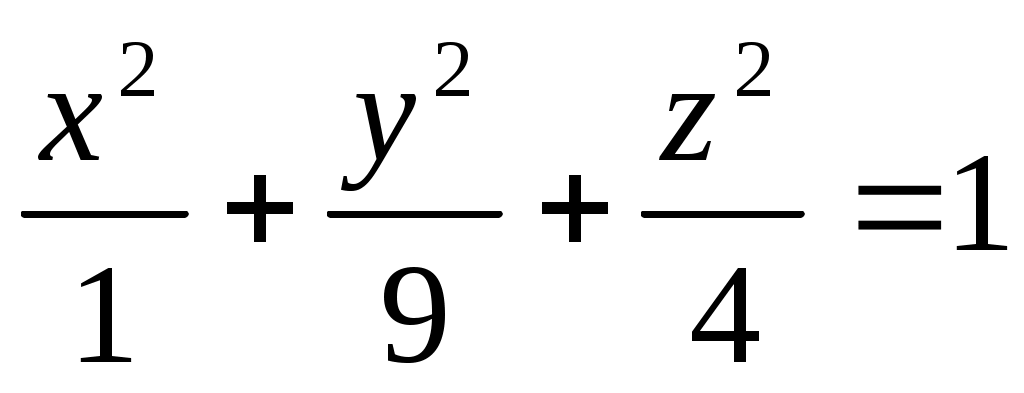 . .
3. 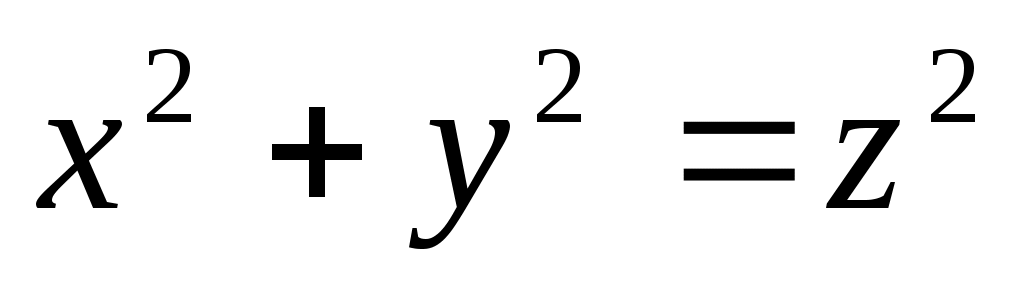 . 4. . 4. 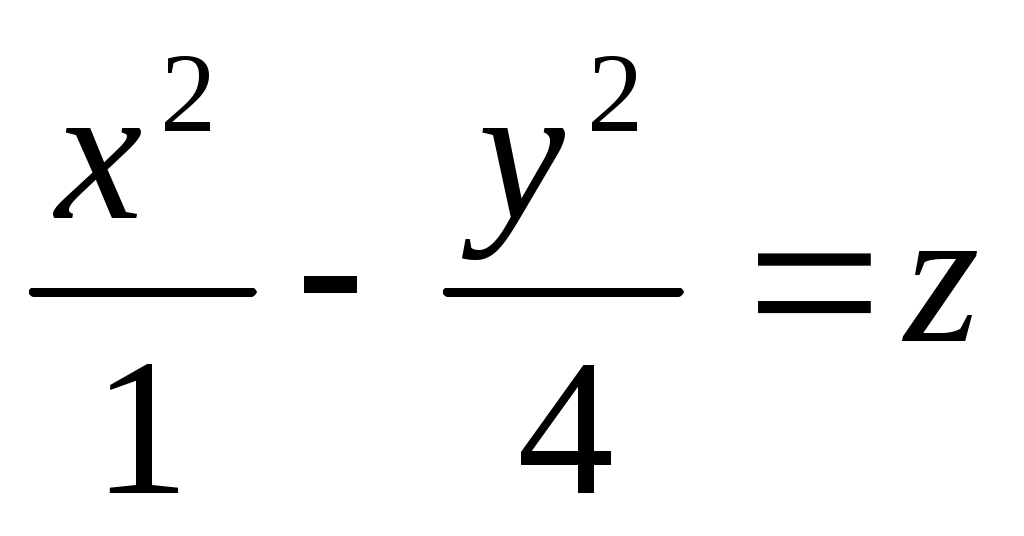 . .
|
85
|
Каноническое уравнение конуса имеет вид:
|
1. 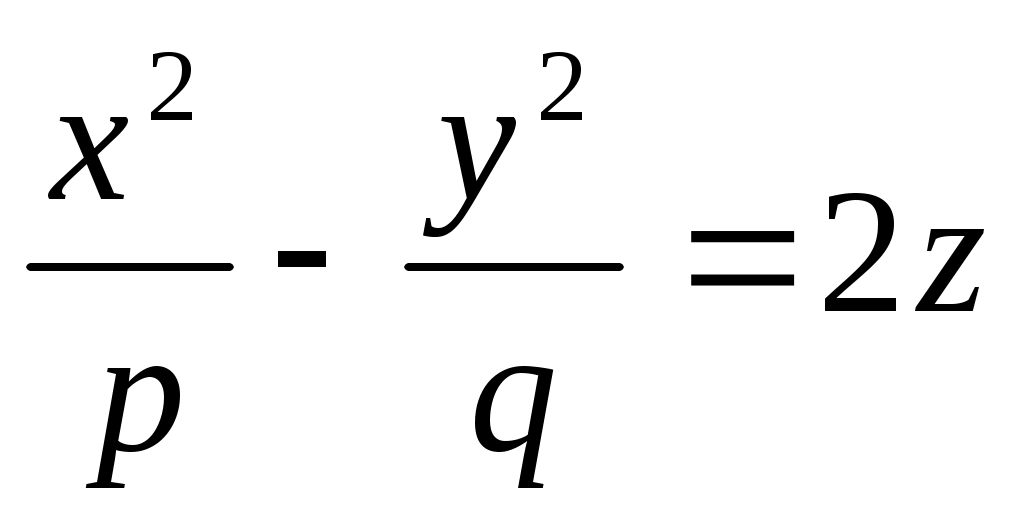 . .
2. 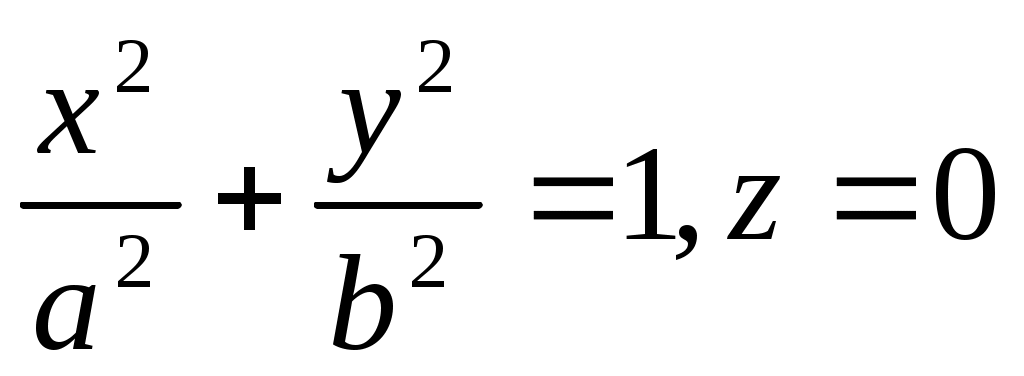 . .
3. 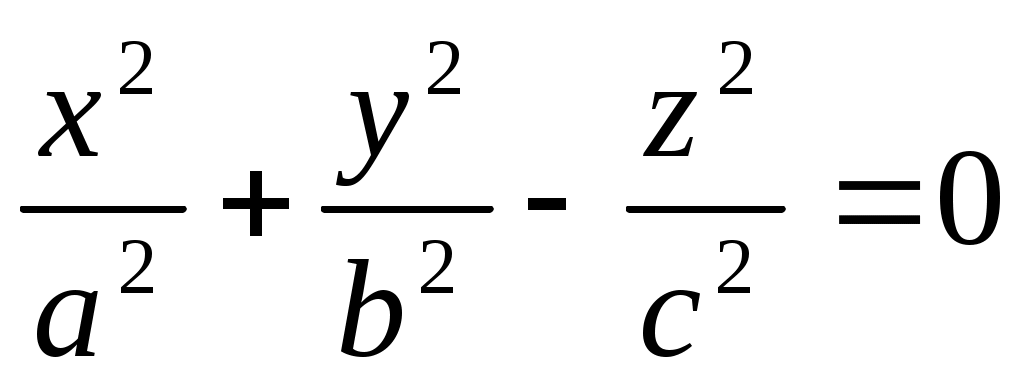 . .
4. 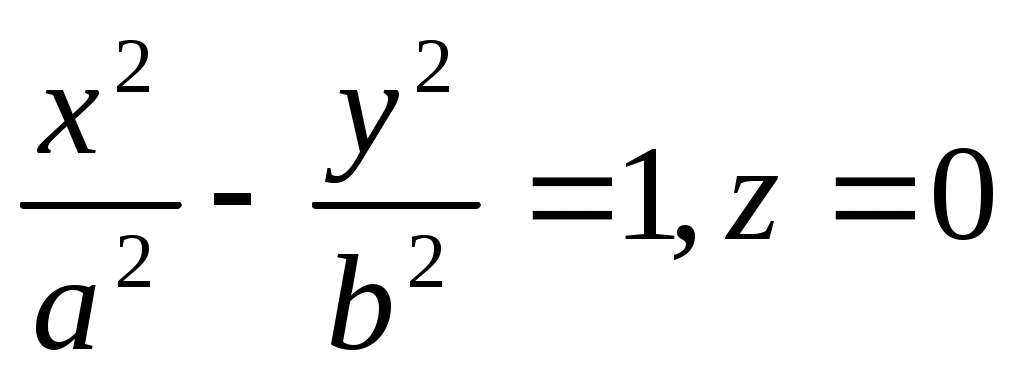 . .
|
86
|
Каноническое уравнение двуполостного гиперболоида имеет вид:
|
1. 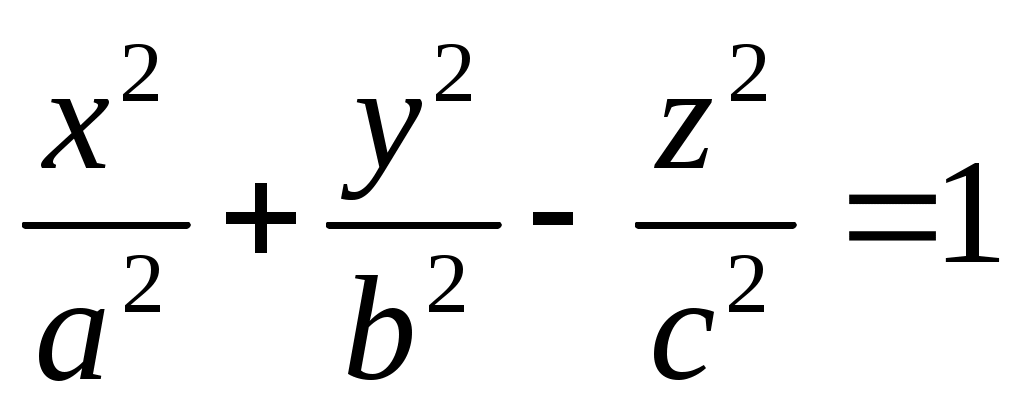 . .
2. 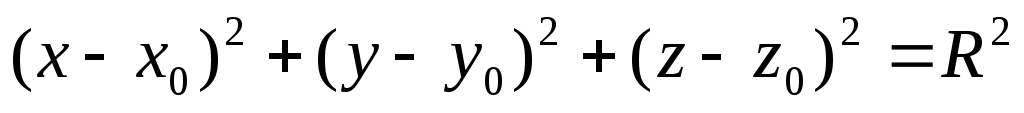 . .
3. 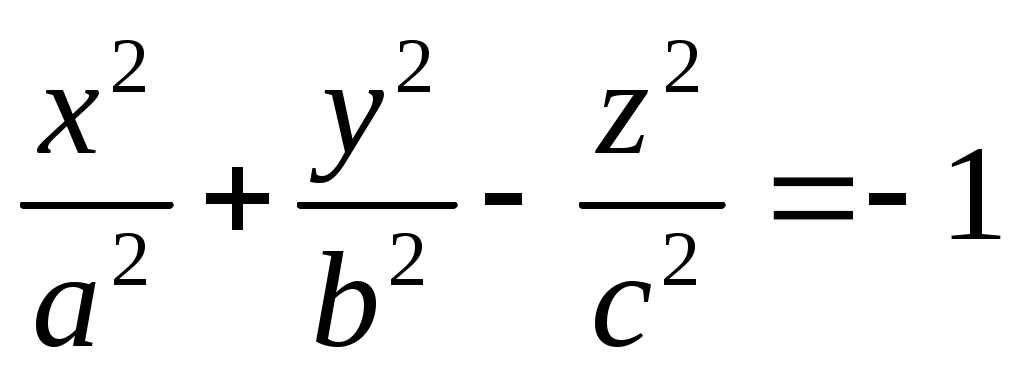 . .
4. 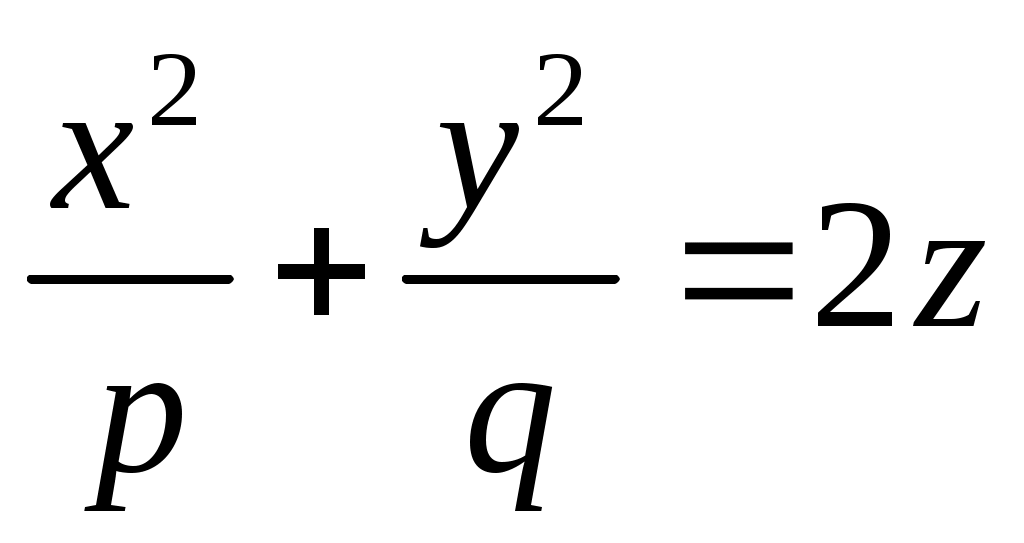 , где , где 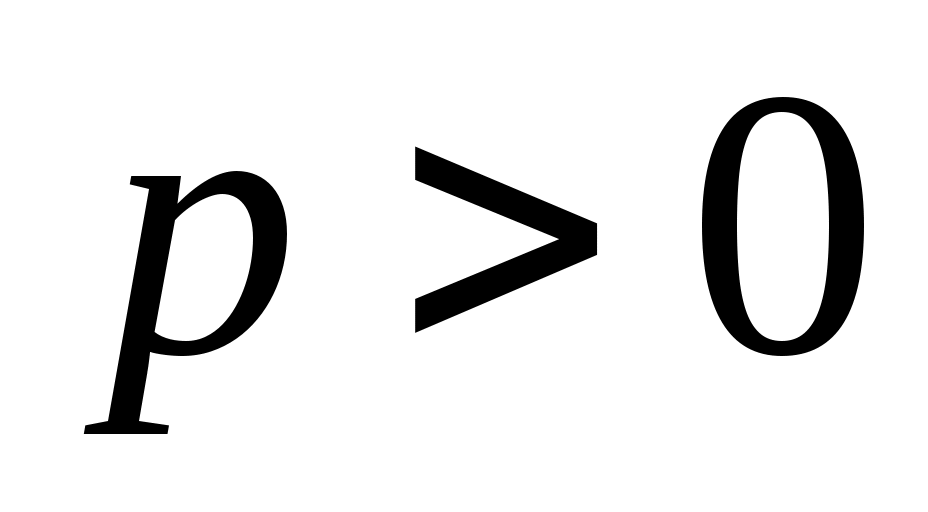 и и 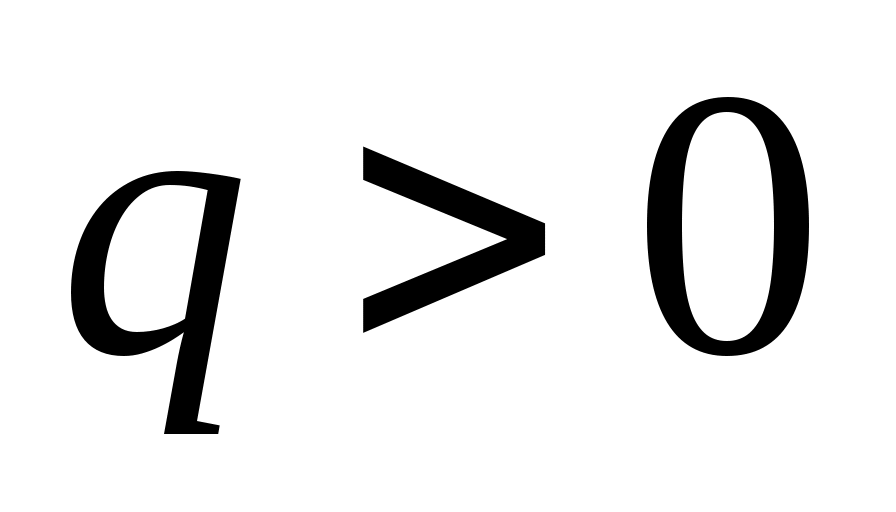 . .
|
87
|
Каноническое уравнение эллиптического параболоида имеет вид:
|
1. 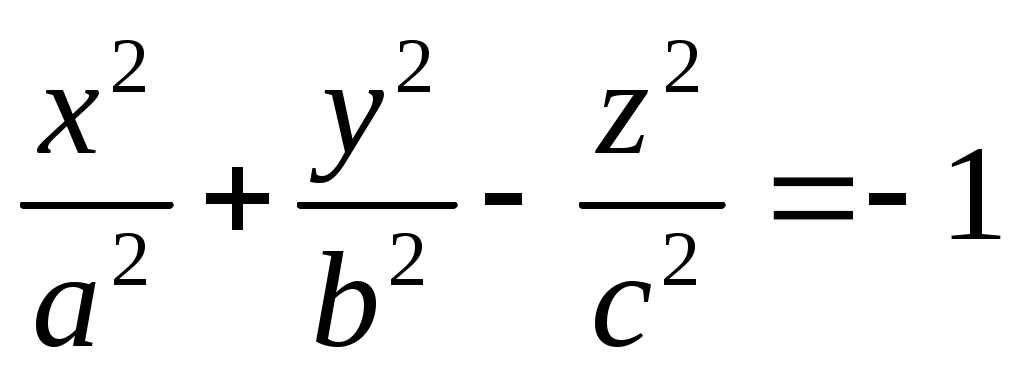 . .
2. 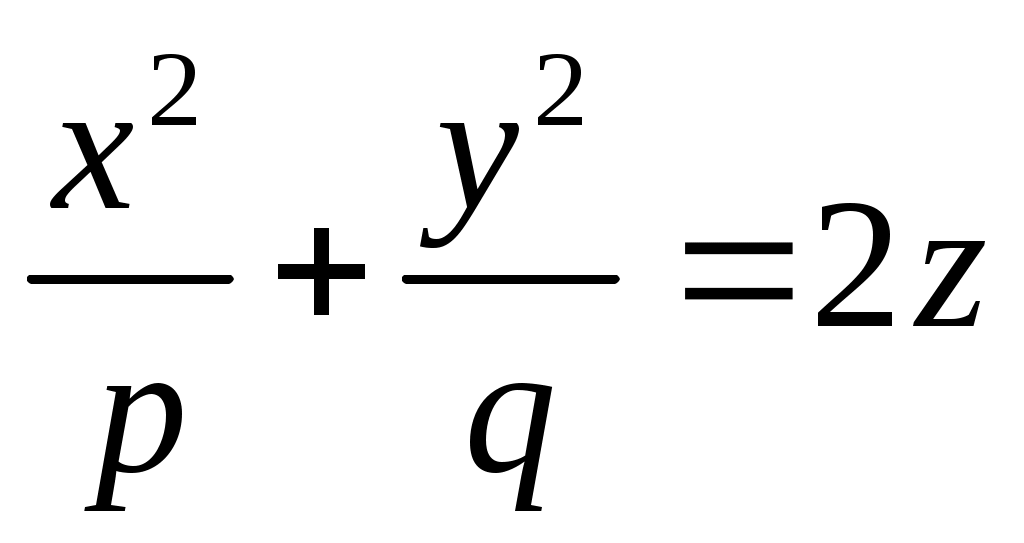 , где , где 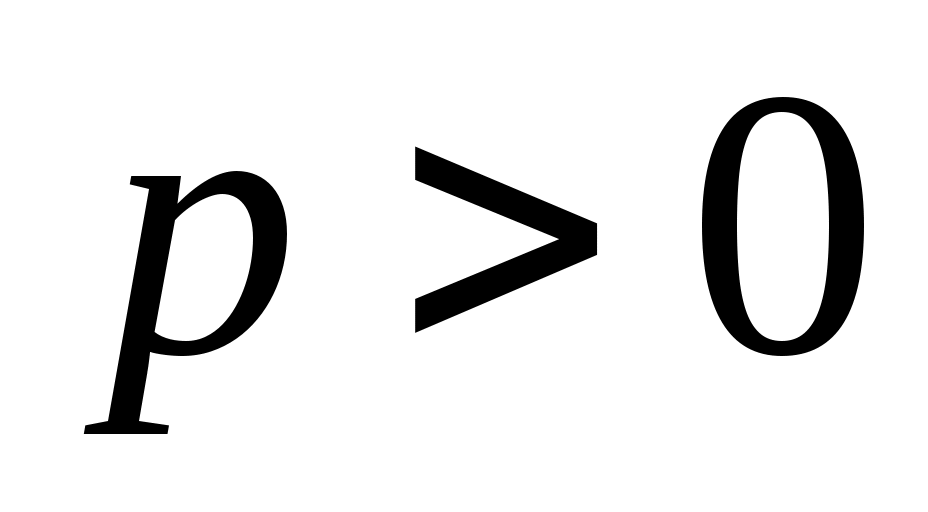 и и 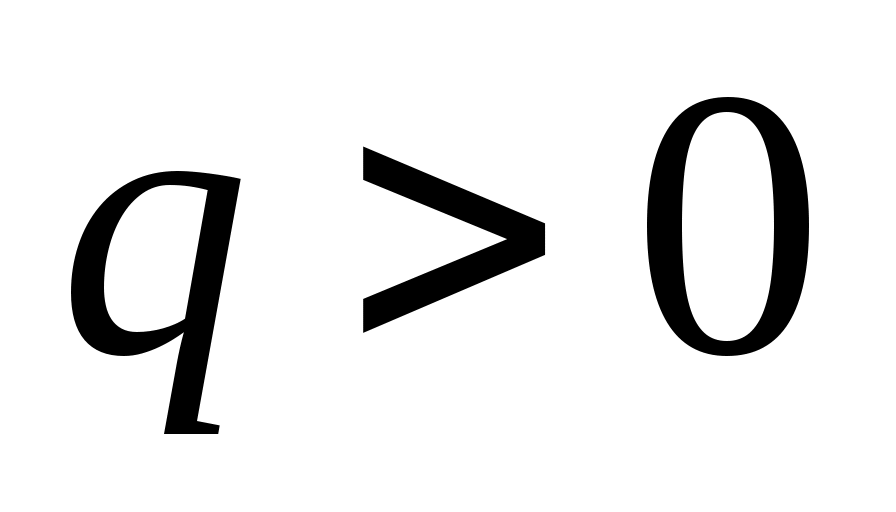 . .
3. 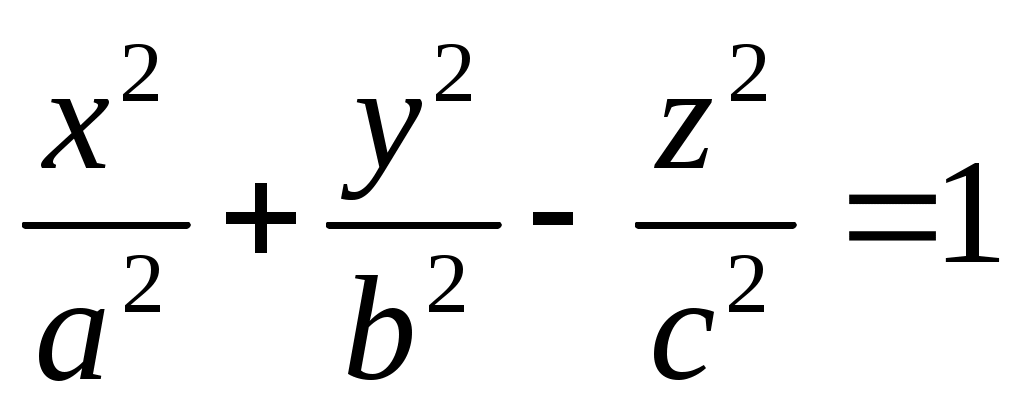 . .
4. 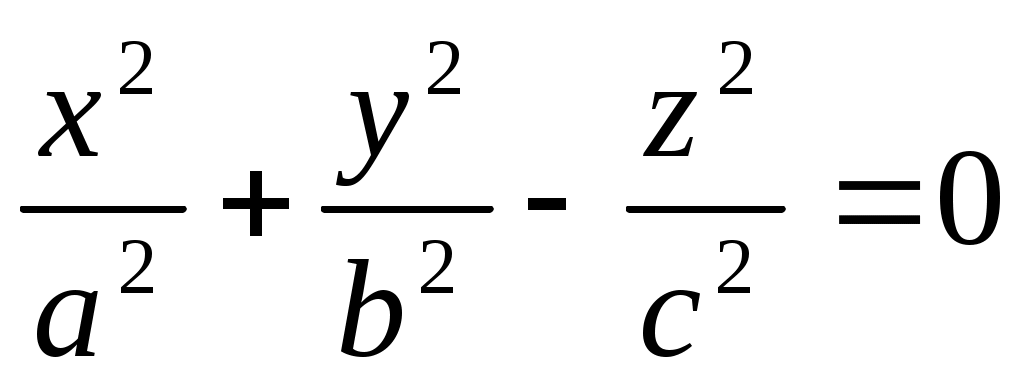 . .
|
88
|
Каноническое уравнение гиперболического параболоида имеет вид:
|
1. 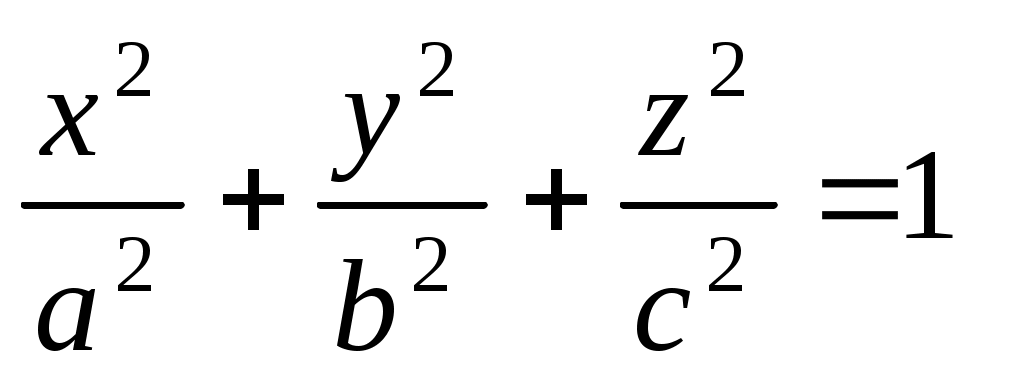 . .
2. 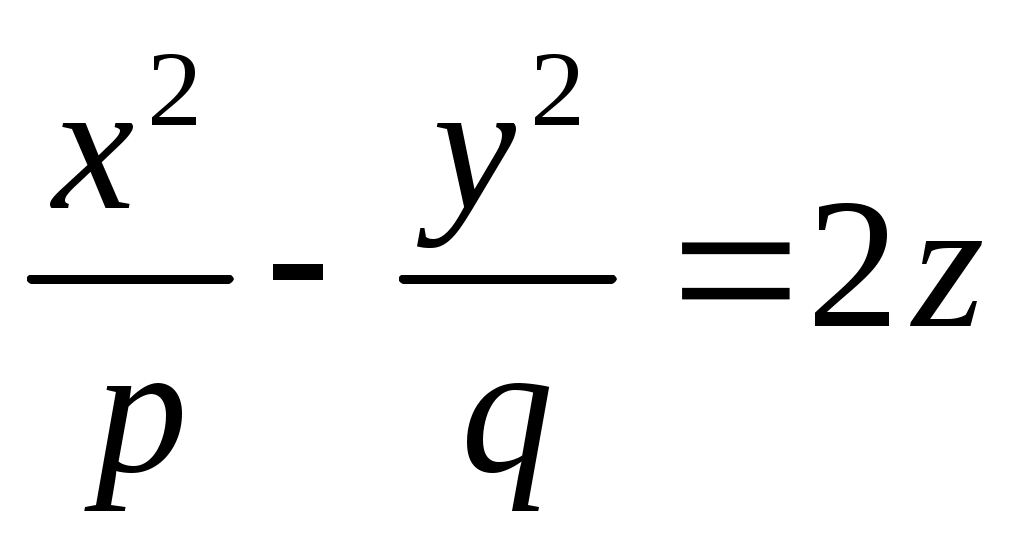 , где , где 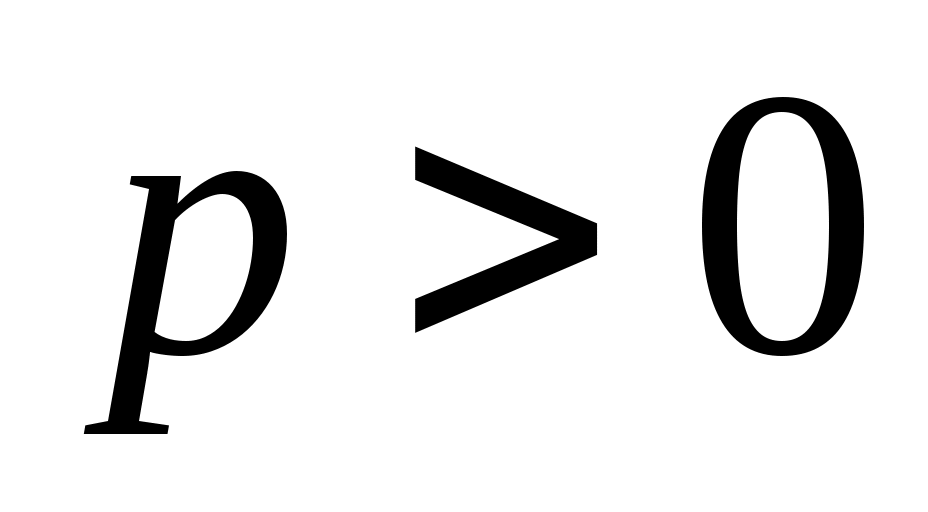 и и 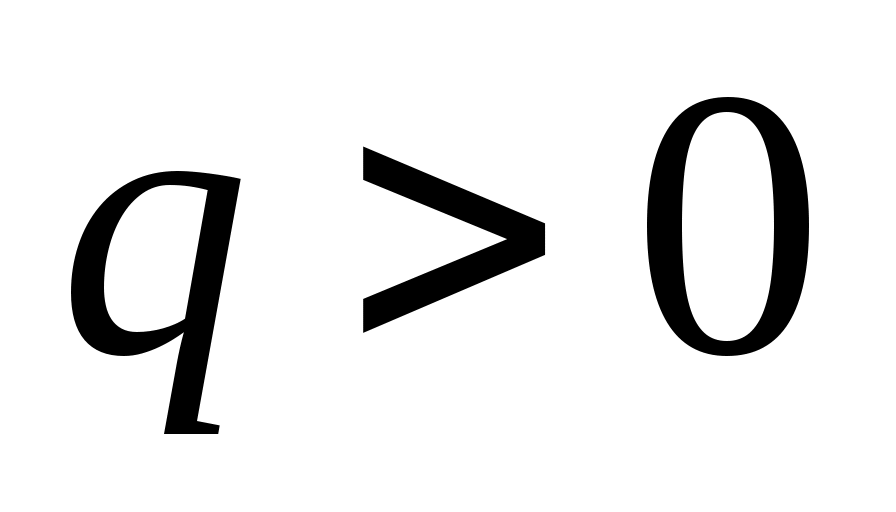 . .
3. 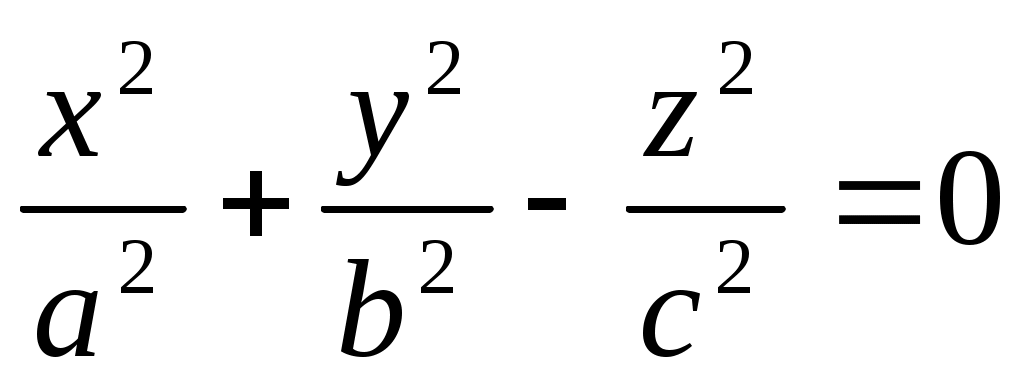 . .
4. 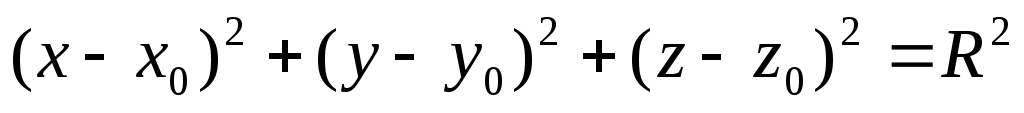 . .
|
89
|
Каноническое уравнение эллиптического цилиндра имеет вид:
|
1. 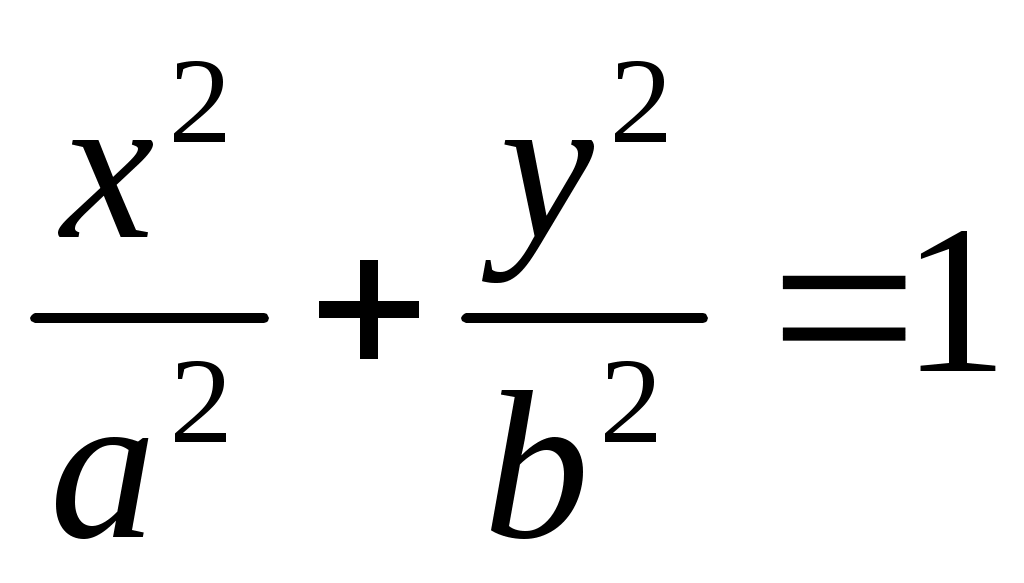 . .
2. 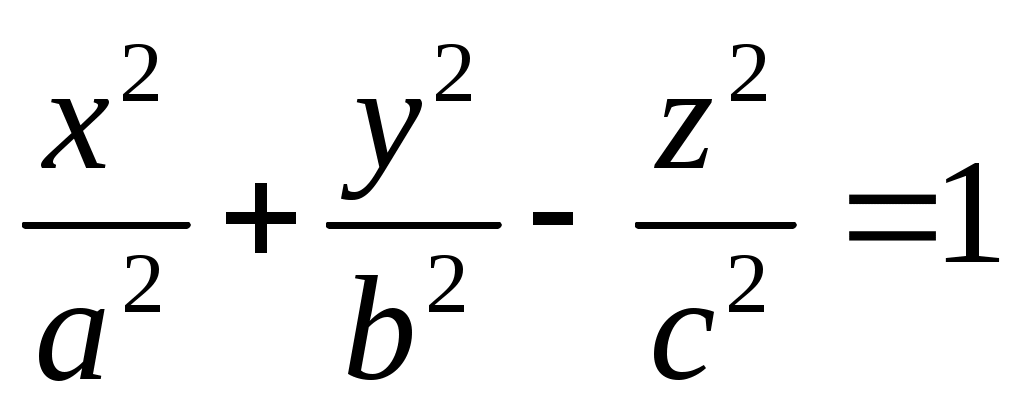 . .
3. 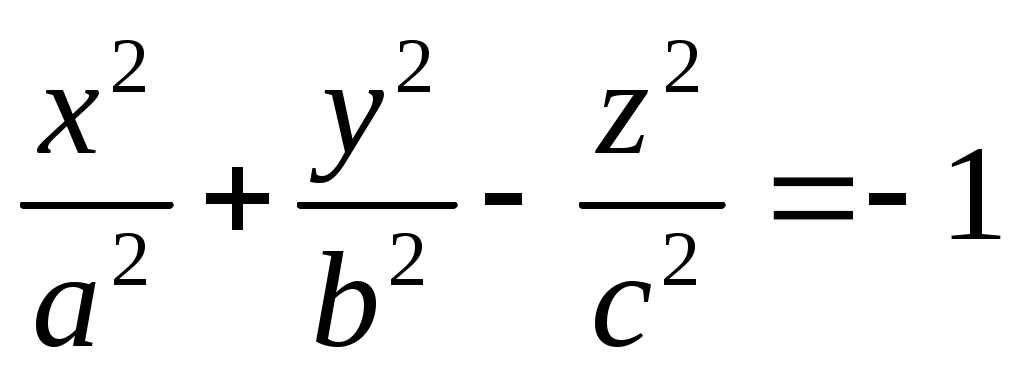 . .
4. 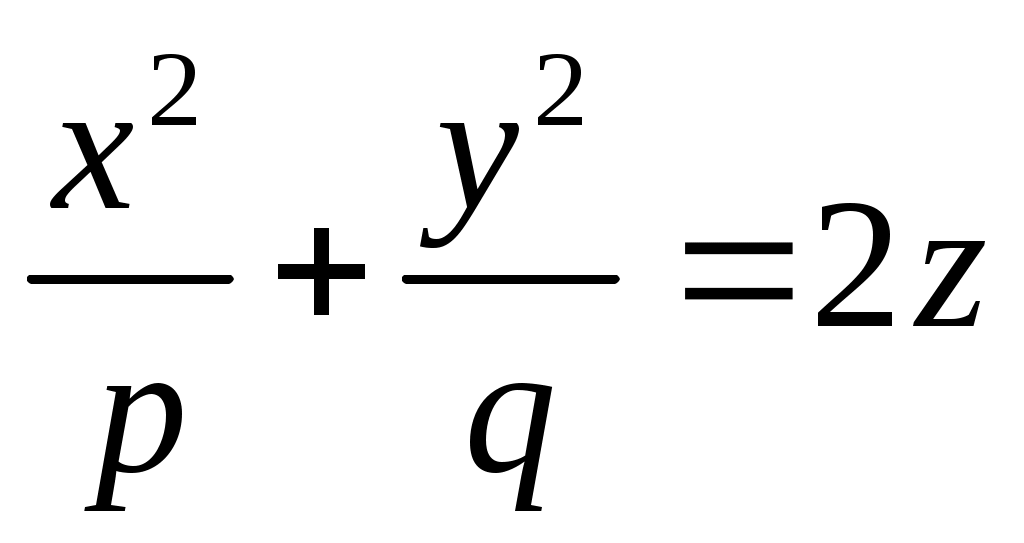 , где , где 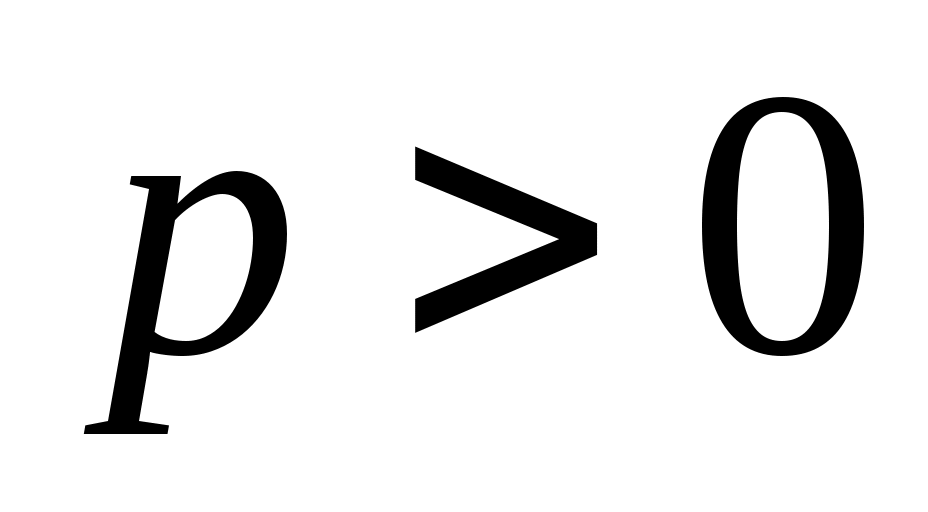 и и 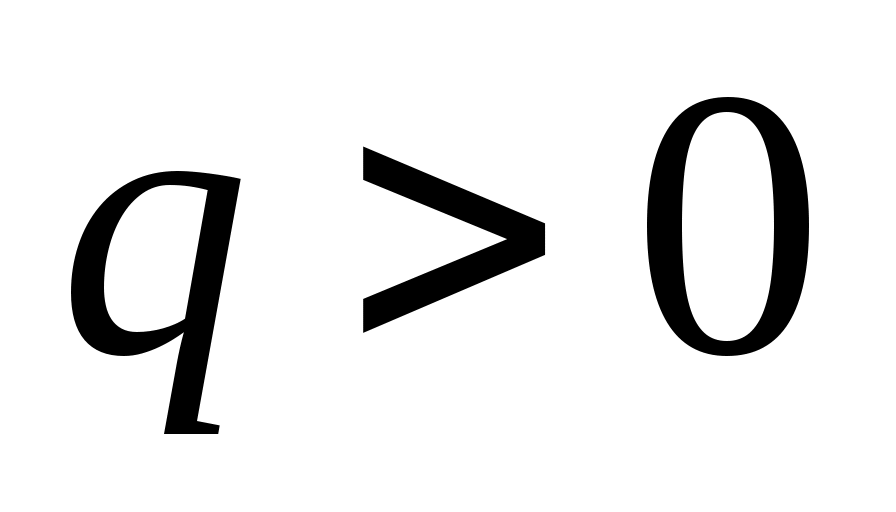 . .
|
90
|
Каноническое уравнение гиперболического цилиндра имеет вид:
|
1. 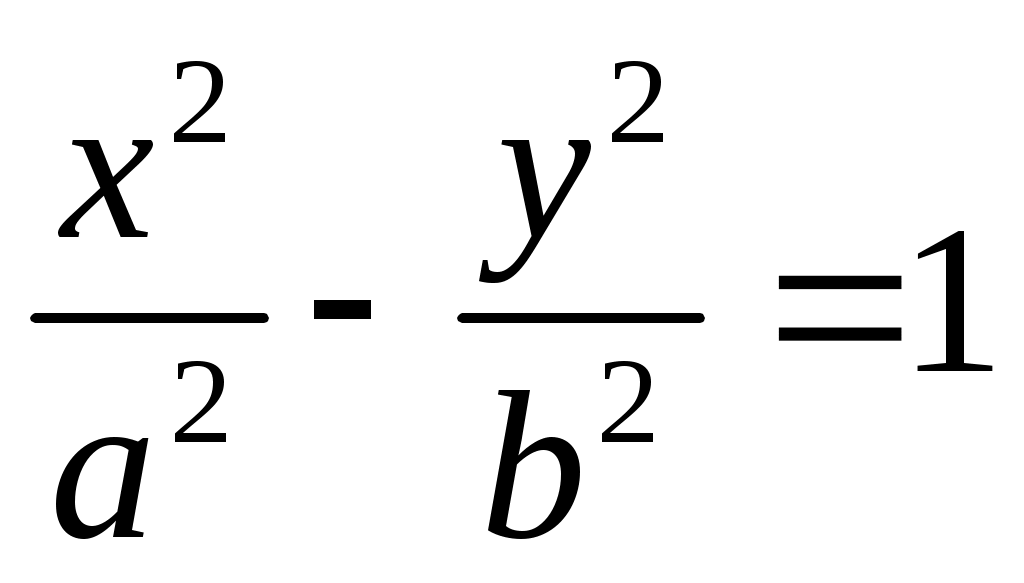 . .
2. 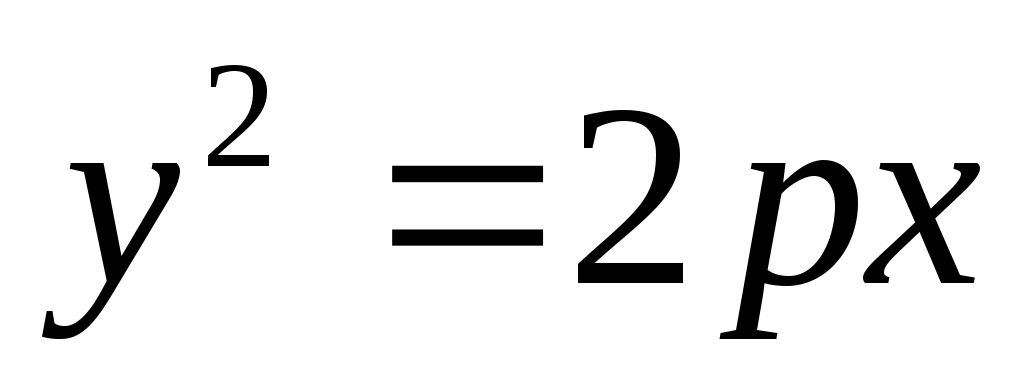 . .
3. 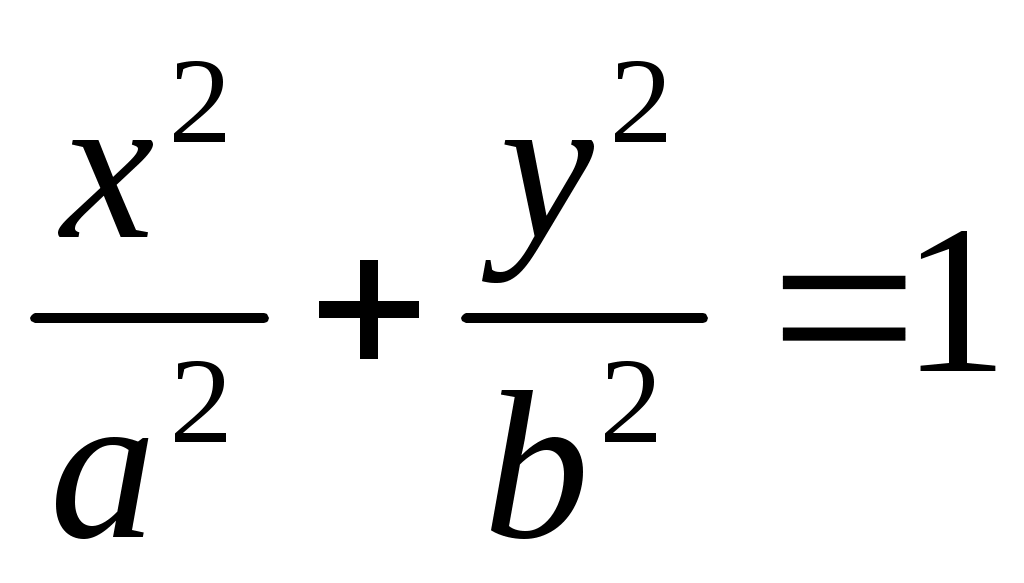 . .
4. 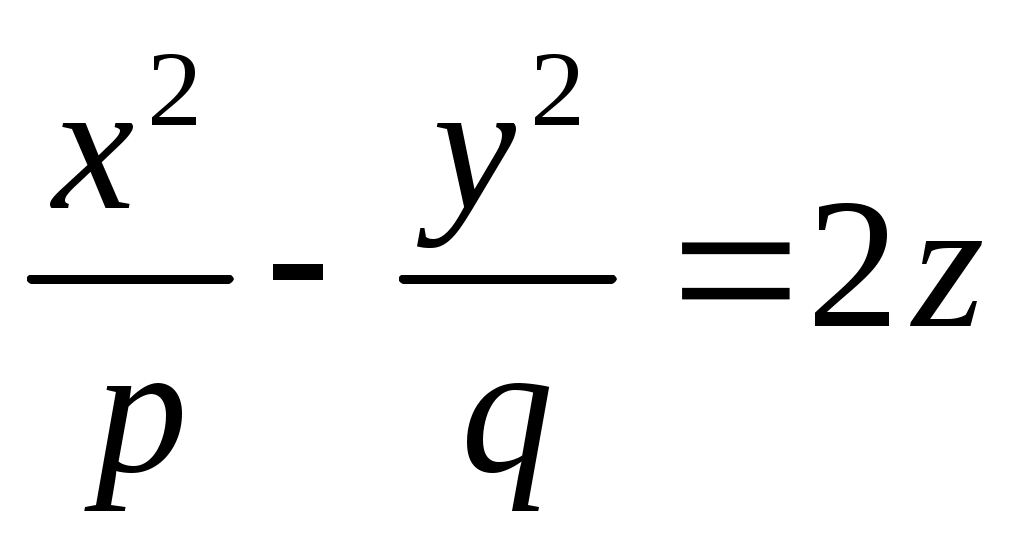 , где , где 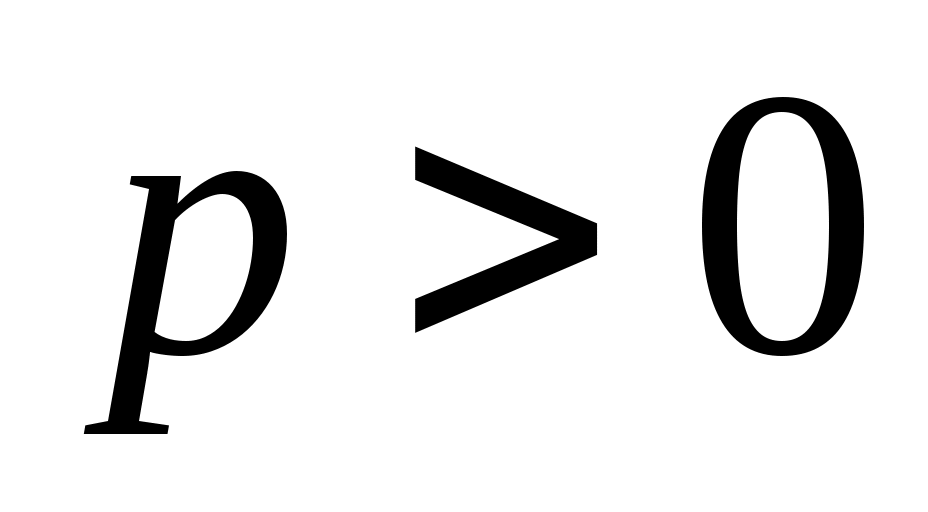 и и 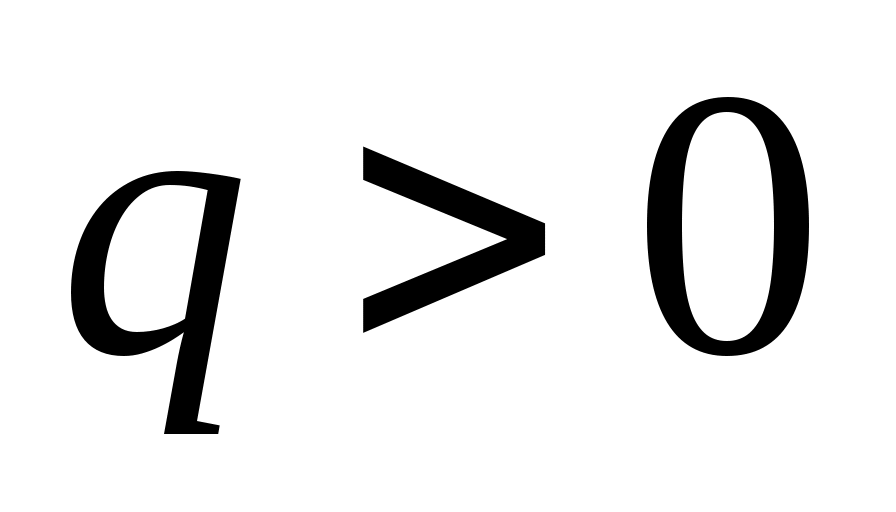 . .
|
91
|
Каноническое уравнение параболического цилиндра имеет вид:
|
1. 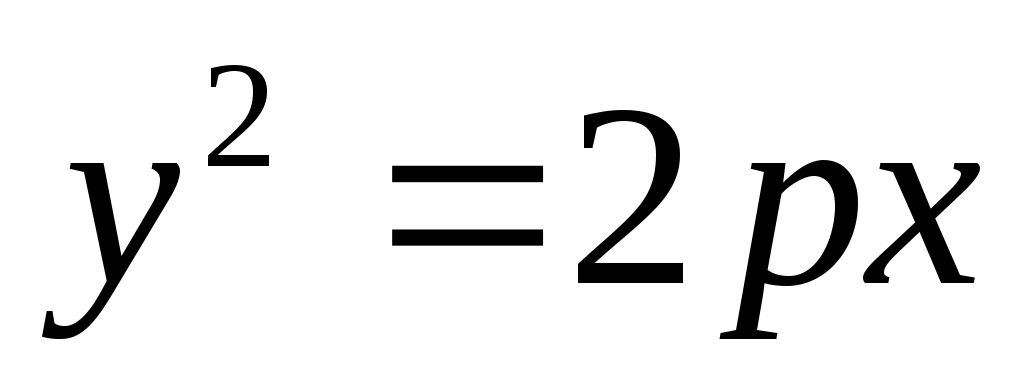 . .
2. 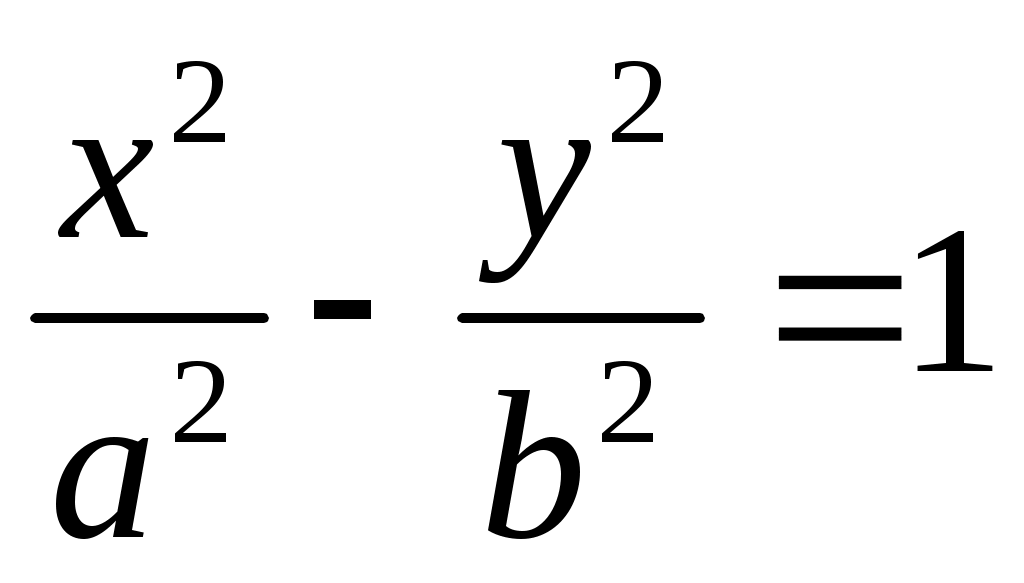 . .
3. 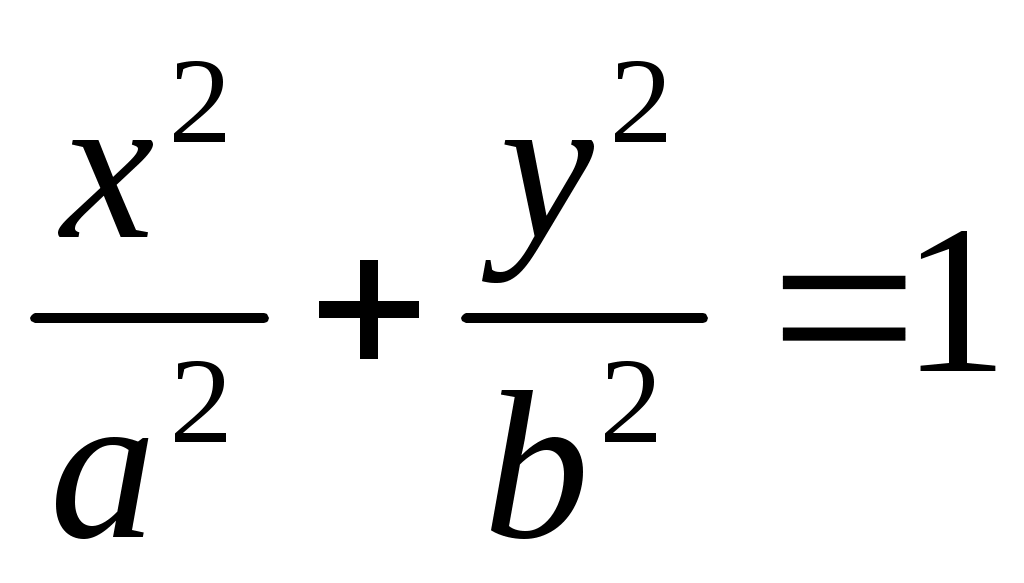 . .
4. 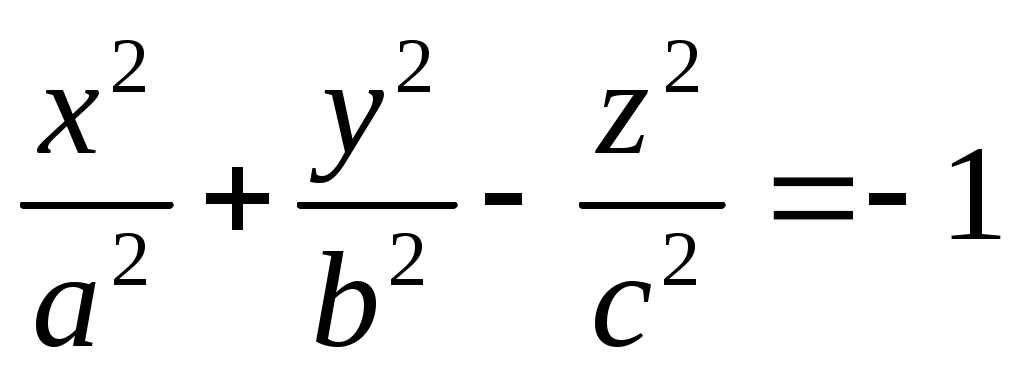 . .
|
92
|
Уравнение поверхности вращения линии 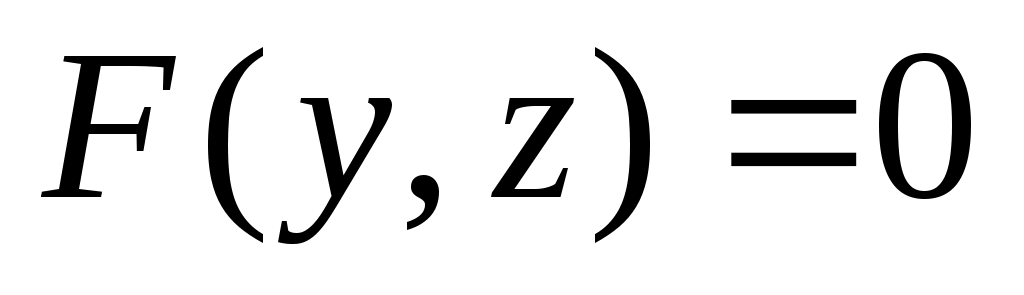 вокруг оси вокруг оси  имеет вид имеет вид
|
1. 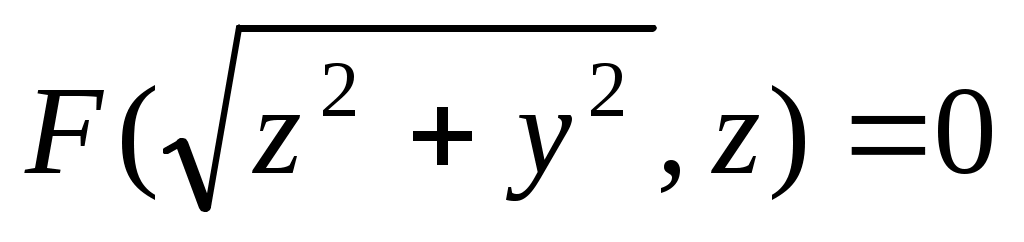 . 2. . 2. 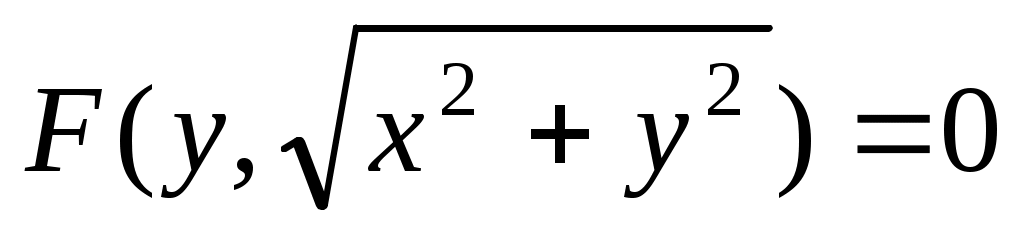 . .
3. 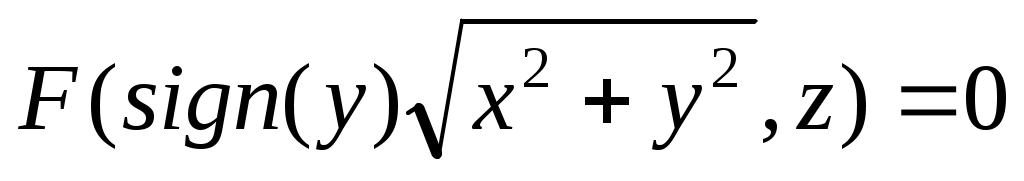 . .
4. 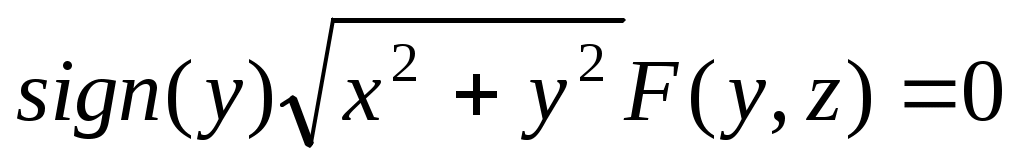 . .
|
93
|
Какое количество параметров используется в каноническом уравнении произвольного эллипсоида?
|
1. Шесть.
2. Два.
3. Три.
4. Четыре.
|
94
|
Какими уравнениями описываются поверхности второго порядка в декартовой системе координат?
|
1. Алгебраическими уравнениями второй степени с тремя неизвестными.
2. Алгебраическими уравнениями третьей степени с двумя неизвестными.
3. Алгебраическими уравнениями первой степени с тремя неизвестными.
4. Тригонометрическими уравнениями второй степени с тремя неизвестными.
|
95
|
Какая поверхность называется конической?
|
1. Это поверхность, которую можно получить движением прямой, сохраняющей две различные неподвижные точки.
2. Это поверхность, которую можно получить движением прямой, перемещающейся параллельно некоторому вектору вдоль направляющей.
3. Это поверхность, которую можно получить движением прямой, сохраняющей одну неподвижную точку, вдоль направляющей.
4. Это ограниченная в пространстве поверхность.
|
96
|
Какая поверхность называется цилиндрической?
|
1. Это поверхность, которую можно получить движением прямой, сохраняющей две различные неподвижные точки.
2. Это поверхность, которую можно получить движением прямой, сохраняющей одну неподвижную точку.
3. Это поверхность, которую можно получить движением прямой, перемещающейся параллельно некоторому вектору вдоль направляющей.
4. Это ограниченная в пространстве поверхность.
|
97
|
Уравнение сферы с центром в точке 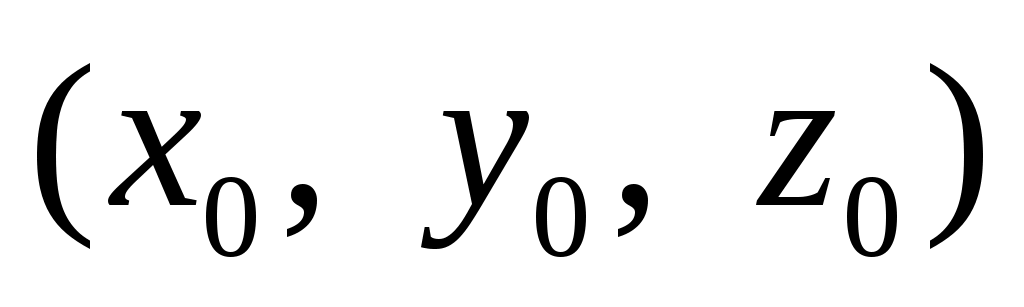 и радиусом и радиусом 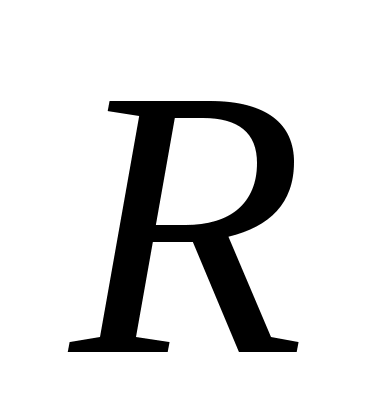 имеет вид: имеет вид:
|
1. 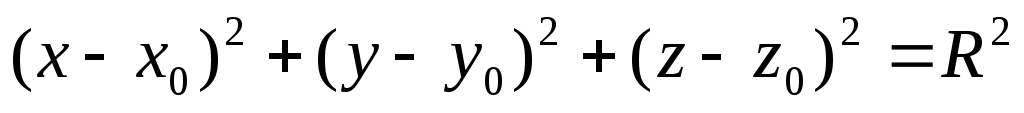 . .
2. 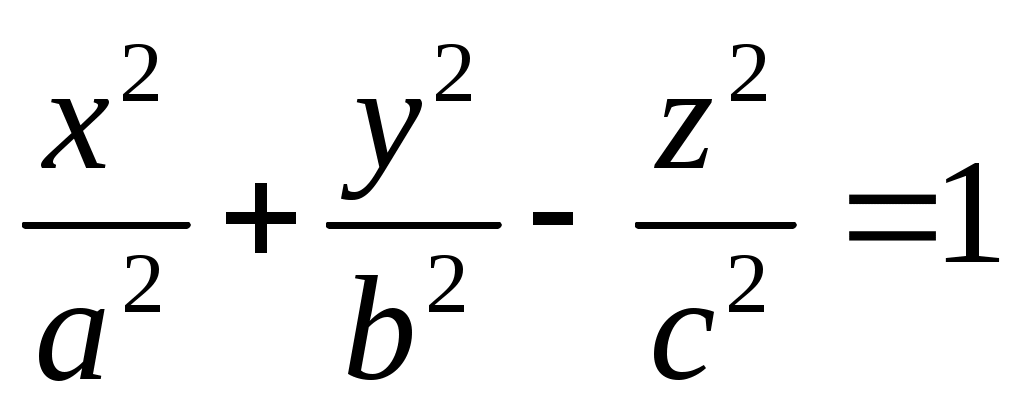 . .
3. 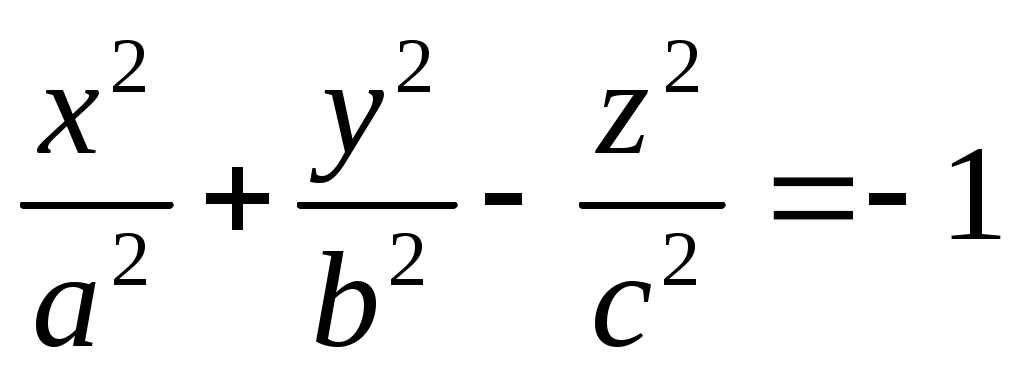 . .
4. 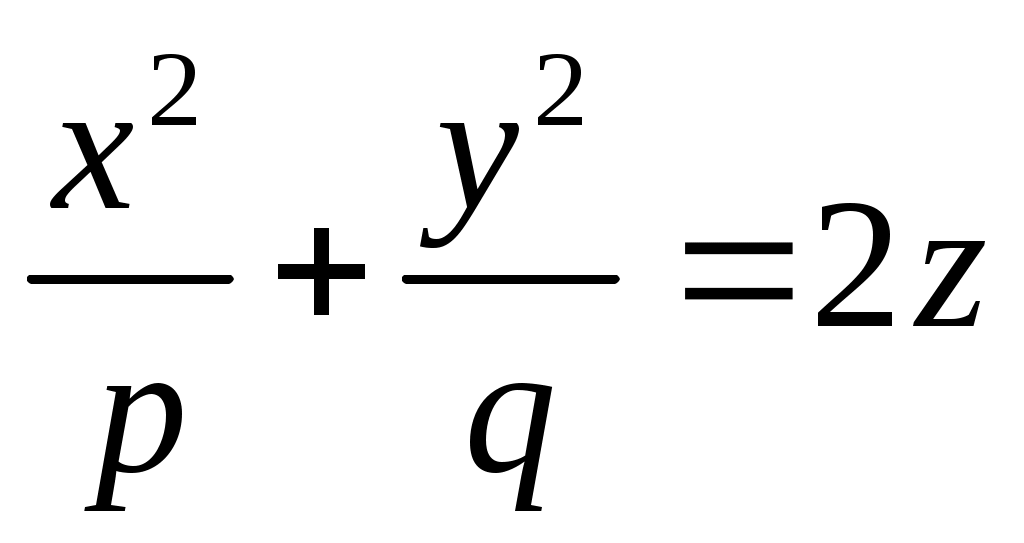 , где , где 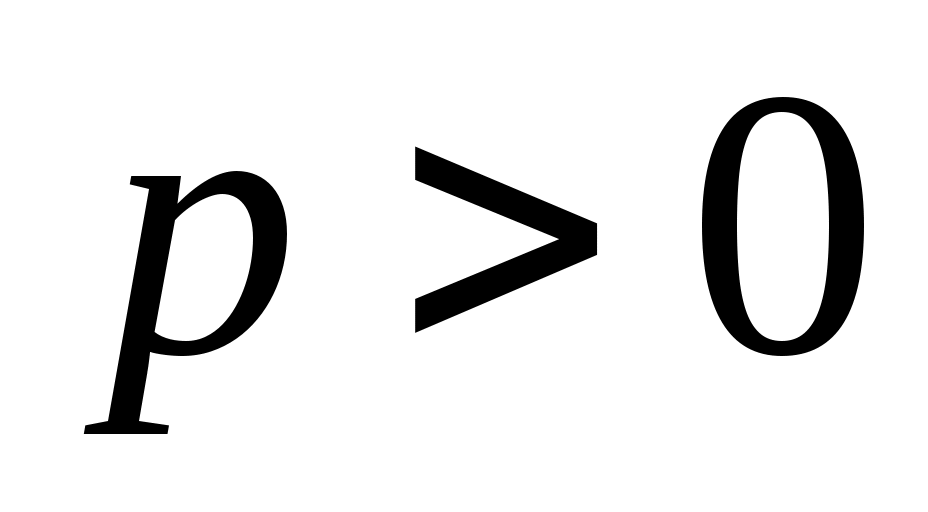 и и 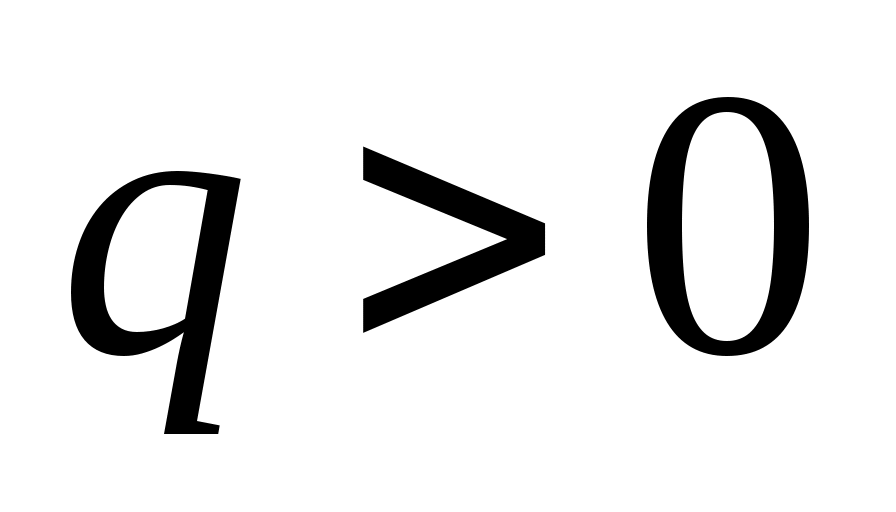 . .
|
98
|
Каноническое уравнение однополостного гиперболоида имеет вид:
|
1. 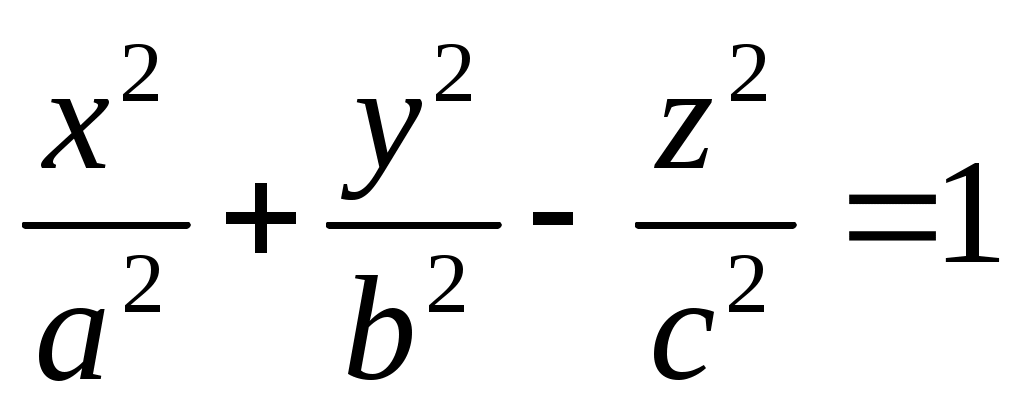 . .
2. 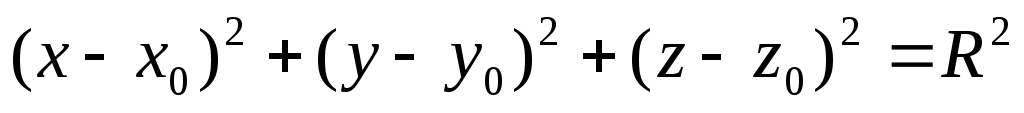 . .
3. 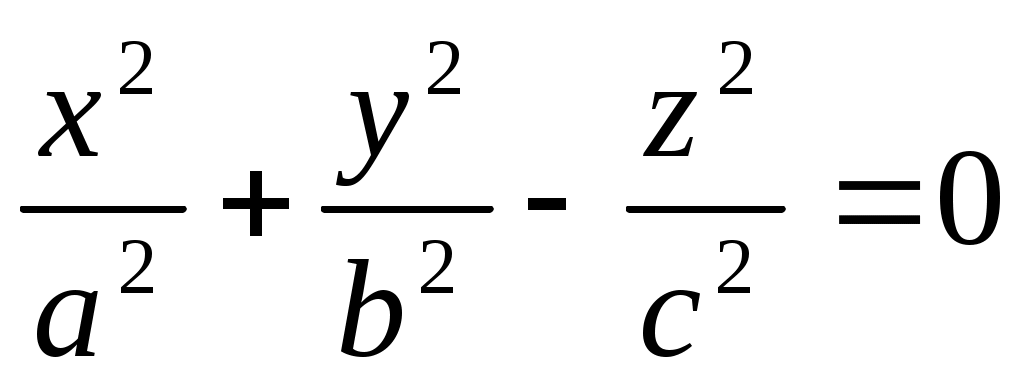 . .
4. 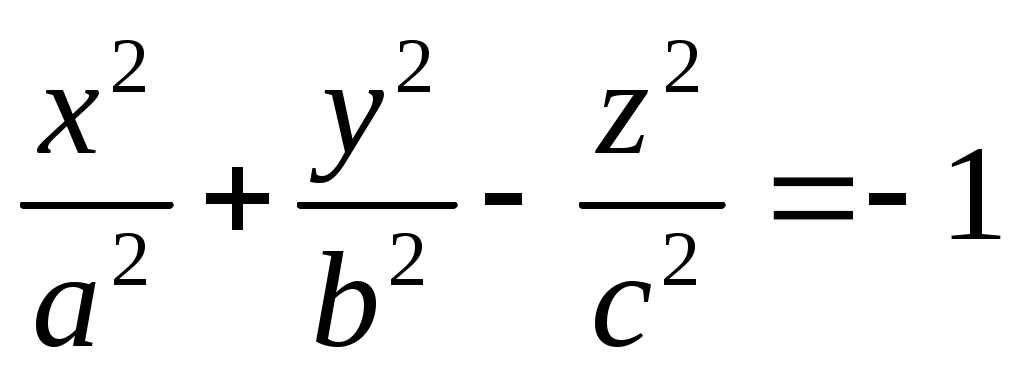 . .
|
99
| Каноническое уравнение эллипсоида имеет вид: |
1. 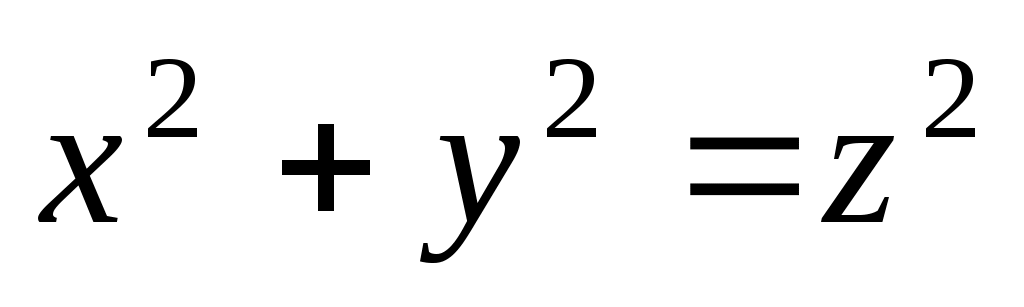 . 2. . 2. 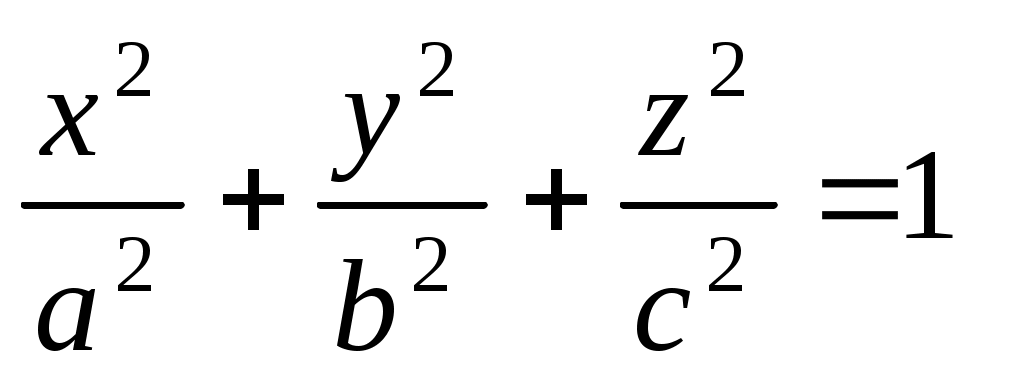 . .
3. 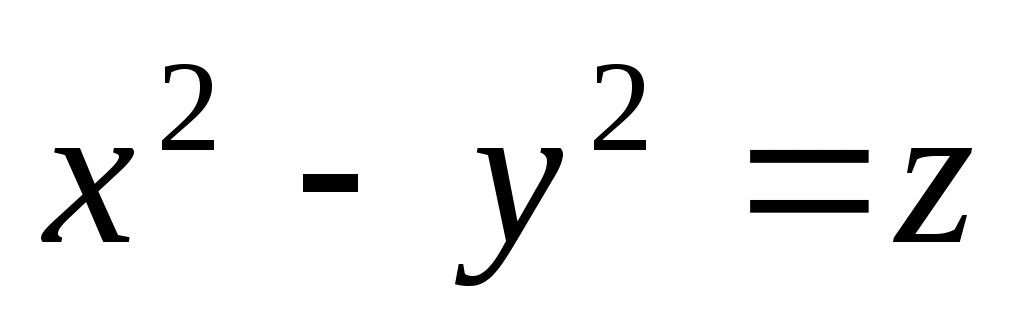 . 4. . 4. 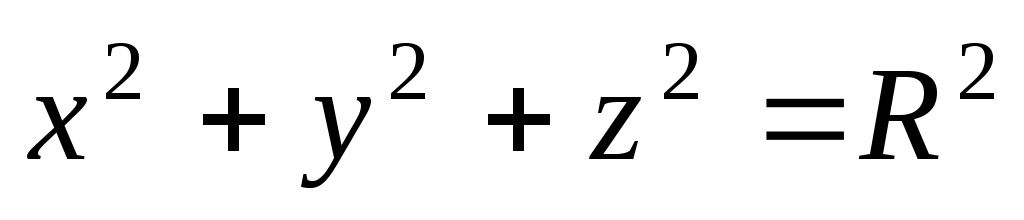 . .
|
100
|
Поверхность (множество) уровня с=1 для функции трех переменных
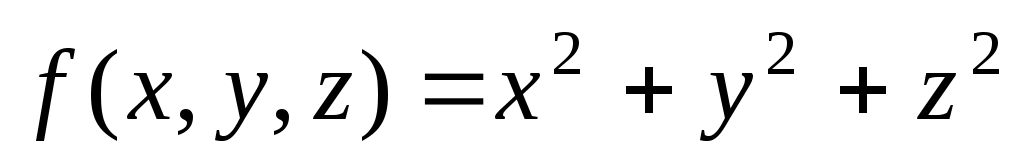 представляет собой: представляет собой:
|
1. единичный круг.
2. единичную окружность.
3. единичный шар.
4. единичную сферу.
|
 Скачать 0.92 Mb.
Скачать 0.92 Mb.