комплексні числа н. Вступ. Поняття про комплексне число
 Скачать 440 Kb.
|
|
КОМПЛЕКСНЕ ЧИСЛО ЯК ОПЕРАТОР ПОВОРОТУ Комплексне число можна розглядати як точку і як вектор. Розглядають ще одне важливе тлумачення комплексного числа. Нехай ми маємо на площині якийсь вектор  (додаток Г) і z – його комплексна координата. Повернемо вектор навколо початку О на кут α (проти руху годинникової стрілки, якщо α>0, і за годинниковою стрілкою, якщо α<0) і розтягнемо цей вектор (не змінюючи його початку) з коефіцієнтом розтягу ρ (розтягуємо «в ρ разів»; при 0<ρ<1 це п еретворення буде стиском). В результаті ми отримаємо новий вектор  ; його комплексну координату позначимо через w. Як же виражається число w через числа z, α, ρ? Нехай z = reіφ. Ясно, що |w|=ρr, φ+α – один із аргументів числа w. Тому, w = ρrei(φ+α) = (ρeiα)·(reiφ). Позначимо через с комплексне число ρeiα. Тоді маємо: w=cz. Таким чином, якщо над вектором виконати операції повороту (на кут α) і розтягу (з коефіцієнтом розтягу ρ), то його комплексну координату z потрібно помножити на комплексне число с=ρeіα. І навпаки, якщо комплексну координату z деякого вектора помножити на комплексне число с= ρeіα, то нове число w=cz буде являти собою комплексну координату вектора  , який може бути отриманим з вектора шляхом повороту (на кут α) і розтягом (з коефіцієнтом ρ).Можна сказати так: кожен комплексний множник с (с≠0) можна тлумачити як оператор повороту (на кут α, що рівний аргументу числа с) і розтягу (з коефіцієнтом розтягу, що дорівнює |с|). Латинське слово «оператор» означає виконавець. Можна сказати, що множник с (у формулі w=cz) перетворює вектор з координатою z у вектор з координатою cz. Ми вияснили геометричну картину: що «робить» комплексний множник с з вектором z, які елементарні геометричні перетворення потрібно виконати над цим вектором, щоб отримати вектор cz. Зрозуміло, що цей висновок легко узагальнити на той випадок, коли початком якого-небудь з даних векторів не є початок координат. Наприклад, якщо вектори  і  мають комплексні координати z i w, причому w=-3iz, то це означає, що після повороту вектора навколо К на кут  радіан (arg (-3i) = ) і розтягу його з коефіцієнтом 3 (|-3і|=3) отримаємо вектор  .Особливо важливий випадок, коли |с|=1. Тоді комплексне число с (воно має вигляд eiα) являє собою оператор повороту. Наприклад, комплексне число і (і=  ) є оператором повороту на кут  радіан (поворот здійснюється в додатному напрямі, тобто проти годинникової стрілки).ЗАСТОСУВАННЯ КОМПЛЕКСНИХ ЧИСЕЛ ПРИ РОЗВ’ЯЗУВАННІ ЗАДАЧ Отже, ми розглянули три різних тлумачення комплексних чисел (комплексне число – точка на площині; комплексне число – вектор; комплексне число – оператор повороту і розтягу). Саме ця багатоликість комплексних чисел робить їх особливо зручним апаратом для розв’язку задач з геометрії і механіки. Приклад 1. ОАВС – квадрат (додаток Д). Вектор  має комплексну координату z = 3-і. Обчислимо комплексну координату вектора  (позначимо її через w1) і вектора  (w2). Розв’язання. Можна одержати , якщо повернути на кут  радіан і потім розтягнути з коефіцієнтом розтягу  . Тому  . Якщо повернути на 900 в додатному напрямі , то отримаємо вектор  . Тому w2=іw1= =і(4+2і)=-2+4і.Приклад 2. Гострий кут при вершині О ромба OZ1Z2Z3 ( О – початок координат ) дорівнює 450, а вершина Z1 має комплексну координату z1=  (вершини O, Z1, Z2, Z3 слідують проти годинникової стрілки). Знайдемо комплексні координати інших вершин ромба.Розв’язання. Позначимо комплексні координати вершин ромба Z1, Z2, Z3 відповідно через z1, z2, z3, вершина О має комплексну координату 0. Вектор  отримуємо з вектора  шляхом повороту (без розтягу) на кут 450 ( радіан). Тому маємо:  =  Оскільки  , то отримаємо: z2=z1+z3=  . Із отриманого тлумачення комплексного множника випливає важливий наслідок: два вектори колінеарні тоді і тільки тоді, коли відношення їх комплексних координат є дійсним числом (і при тому додатнім, якщо вектори співнапрямлені, і від’ємним, якщо вектори протилежно напрямлені). Дійсно, нехай вектори  і  мають комплексні координати z=reіφ, w=ρeіθ. Якщо вектори і співнапрямлені, то θ=φ ( з точністю до цілого кратного числа 2π), і тому w/z = ρ/r >0. Якщо ж вектори і протилежно напрямлені, то θ=φ+π (з точністю до цілого кратного числа 2π), і тому w/z =-ρ/r <0.Якщо і не колінеарні, то θ-φ≠kπ і число w/z не є, очевидно, дійсним.Приклад 3. Зобразимо на комплексній площині точки Z1, Z2, Z3 з координатами 8+13і, 13+21і, 21+34і. Чи лежать вони на одній прямій? Розв’язання. При розгляді вказаних точок складається враження, що вони лежать на одній прямій. Перевіримо це наступним міркуванням. Точки Z1, Z2, Z3 тоді і тільки тоді лежать на одній прямій, коли вектори  і  колінеарні, а це буде тільки в тому випадку, коли відношення їх комплексних координат z і w являє собою дійсне число. Але z = z2-z1=5+8i, w=z3-z2=8+13i,   . А це не дійсне число. Отже, точки Z1, Z2, Z3 не лежать на одній прямій. Неважко знайти кут α між векторами і : tg α = , тоді α=0024/.Приклад 4. Одного разу юним слідопитам дістався такий запис: «Я, пірат Кід, на прізвисько Математик, закопав скарб на великій лісовій галявині, де ростуть берізка В, старий дуб D, і на відстані біля 50 метрів від нього велика сосна С. Точку В я подумки повернув навколо дуба D на 900 проти напрямку руху Сонця, а відносно сосни на 900 за напрямком руху Сонця. В результаті я отримав дві точки: D1 і С1, середину К відрізка D1C1 я вибрав місцем для скарбу.» Діти знайшли галявину і за допомогою комплексних чисел знайшли скарб. Як вони це зробили? (додаток Е) Розв’язання. Будемо вважати, що точки В, С, D, С1, D1, К (див рисунок) задані на координатній площині і b, с, d, c1, d1 i k їх координати. Тоді d1-d=i(b-d), c1-c=-i(b-c), k=  (c1+d1), звідки k=(c+d)+ +i . Число m=(c+d) – це координата середини М відрізка DC, а число p=(c-d) – координата вектора  . Оскільки, k-m=ip, то ясно, що точку К можна отримати з точки С, якщо останню повернути навколо точки М в додатному напрямі (проти напряму руху Сонця) на 900.Отже, можна зробити висновок, що одних знань про дійсні числа не вистачає для повного вивчення математики. Є багато інших цікавих розділів, вивчення яких є дуже важливим для нашого подальшого життя. І, саме одним із цих розділів, є розділ математики про комплексні числа. ВИСНОВКИ Комплексні числа є повноцінним розділом сучасної математики, без них не обходяться науки, що пов’язані з математикою. Таким чином, за допомогою теорії функцій комплексної змінної, яка розвинулася на основі комплексних чисел, було розв’язано багато проблем аеро- і гідродинаміки, теорії пружності, радіотехніки та багатьох інших. Комплексні числа вивчати цікаво і без них сучасна математика була б більш складною, нудною і не такою захопливою. ВИКОРИСТАНА ЛІТЕРАТУРА 1. Математический энциклопедический словарь. Москва, «Советская энциклопедия», 1988 г. 2. Франтішек Латка. Математичний міні лексикон. Львів. Видавництво «Світ», 1990 р. 3. М. Шкіль, З. Слєпкань, О. Дубинчук. Алгебра і початки аналізу. 10-11 кл. Київ. «Зодіак-еко», 2000 р. 4. М. Балк, Г. Балк, А. Полухин. Реальные применения мнимых чисел. Киев. «Радянська школа», 1988 г. 5. М.Б. Балк, Н.Я. Виленкин, В.А. Петров. Математический анализ. Теория аналитических функций. Москва. Просвещение, 1985 г. 6. С.Г. Гиндикин. Рассказы о физиках и математиках. Москва. Наука. 1985 г. 7. Р.С. Гутер, Ю.Л. Полунов. Джироламо Кардано. Москва. Знание. 1980 г. 8. И.Л. Кантор, А.С. Солодовников. Гиперкомплексные числа. Москва. Наука. 1973 г. 9. А.И. Кострикин. Введение в алгебру. Москва. Наука. 1977 г. 10. А.И. Маркушевич. Комплексные числа и конформные отображения. Москва. Наука. 1979 г. 11. А.И. Маркушевич, Л.А. Маркушевич. Введение в теорию аналитических функций. Москва. Просвещение. 1977 г. 12. Л.С. Понтрягин. Обобщения чисел. Москва. Наука. 1986 г. 13. И.М. Яглом. Комплексные числа и их применения в геометрии. Москва. Физматгиз. 1963 г. ДОДАТКИ Додаток А Y 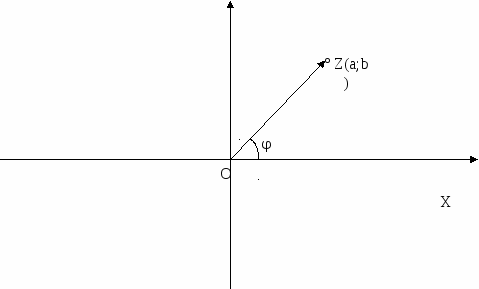 Додаток Б 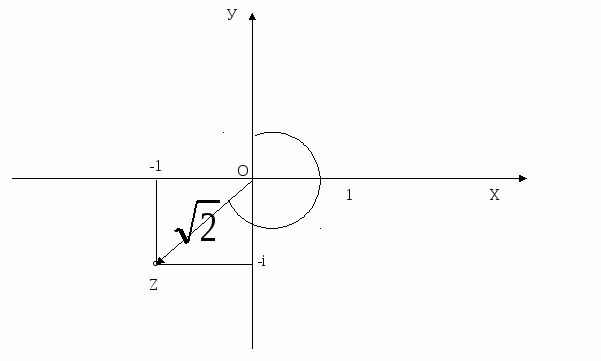 Додаток В 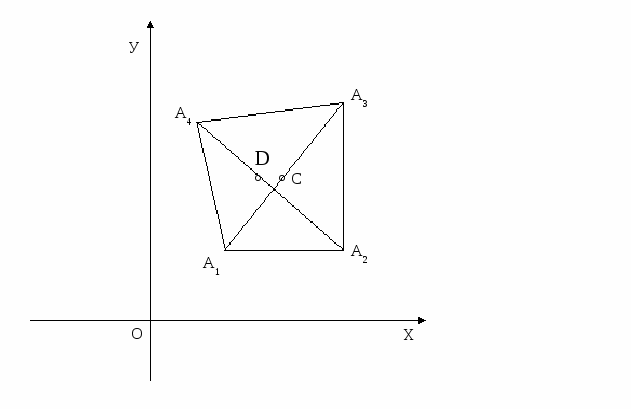 Додаток Г  Y  Z α  O Х Додаток Д 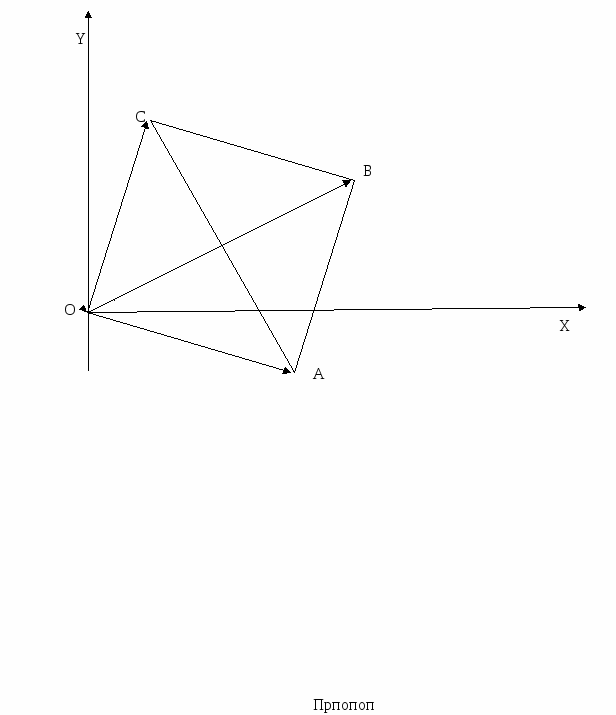 Додаток Е 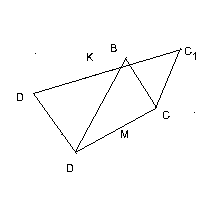 |