решение. 1 мат. Вступительные испытания по математике
 Скачать 46.95 Kb. Скачать 46.95 Kb.
|
|
ВСТУПИТЕЛЬНЫЕ ИСПЫТАНИЯ ПО МАТЕМАТИКЕ: Ответ: 13 часов. Ответ: наибольшая среднесуточная температура в период с 17 по 24 марта – 3 градуса Цельсия. Ответ: 24000 руб. (Во всех трех вариантах стоимость равна 24 000 руб.) Ответ: наименьшая стоимость покупки составляет 178200 руб. Поставщик A: стоимость бруса - 4200 · 40 = 168 000 руб., с доставкой: 168 000 + 10 200 = 178 200 руб. Поставщик Б: стоимость бруса - 4800 · 40 = 192 000 руб., что превышает 150 000 руб., поэтому доставка бесплатная. Стоимость заказа 192 000 руб. Поставщик В: стоимость бруса - 4300 · 40 = 172 000 руб., с доставкой: 172 000 + 8200 = 180 200 руб. Ответ: 26 см2 Ответ: 6 см2 Ответ: 0,6 Число благоприятных исходов n=25-10=15; Вероятность события: P=15/25=0,6. Ответ: 0,46 Ответ: x= -1. 23-2x=25; 3-2x=5; x= -1. Ответ: x= 8. 9-5+x=93; -5+x=3; x=8. Ответ: 56о.  B       ? C  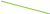    O  A R – радиус окружности; Используем теорему синусов: 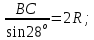 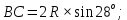 Используем теорему косинусов: 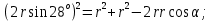  Используем формулу двойного косинуса: 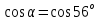 . .Ответ: 68о. (по аналогии с 11 заданием) Ответ: 2 см. V1 = πR2 ∙ h = πR2 ∙ 8; V2 = π (2R)2 ∙ h; V1 = V2; πR2 ∙ 8 = π (2R)2 ∙ h; 8 = 22 ∙ h; h=2. Ответ: 3 точки (X1, X6, X7) Значение производной в своём геометрическом смысле есть тангенс угла наклона касательной. Такой коэффициент положительный когда касательная к графику функции стремится вверх. Ответ: 5 см. V1 = πR2 ∙ h = πR2 ∙ 245; V2 = π (7R)2 ∙ h; V1 = V2; πR2 ∙ 245 = π (7R)2 ∙ h; 245 = 72 ∙ h; h=5. Ответ: sin α = - 0,6 Основное тригонометрическое тождество: sin²α + cos²α = 1; sin²α = 1 - cos²α = 1 - 0.8² = 1 - 0.64 = 0.36; sin α = √0.36 или sin α = - √0.36; sin α = - 0,6 (Так как в третьей и четвертой четвертях, синус – отрицательный). Ответ: 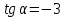 . .Из тождества  ; ;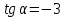 . (Так как в четвертой четверти, тангенс – отрицательный). . (Так как в четвертой четверти, тангенс – отрицательный).Ответ: 400 градусов.  Ответ: 5 Ом. Необходимо найти сопротивление 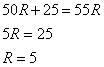 Ответ: 10. Так как конус вписан в сферу, то образующие конуса пересекаются под углом в 90 градусов и образуют вместе с диаметром равнобедренный прямоугольный треугольник. Найдем длину образующей конуса из этого прямоугольного треугольника по теореме Пифагора, получим: 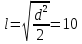 Ответ: скорость течения реки равна 5 км/ч. Пусть x км/ч — скорость течения, тогда скорость теплохода по течению равна 15+x км/ч, а скорость теплохода против течения равна 15-x км/ч. На весь путь теплоход затратил 40 – 10 = 30 часов. Тогда: Ответ: x= - 4. Берем первую производную: y' = 1/(x+5)^5 * 5(x+5)^4 - 5 = 5/(x+5) – 5; Так как нас интересует экстремум, то ищем такие иксы, в которых производная равна нулю: y'=0 => 5/(x+5) - 5 =0; Решив это уравнение, получаем: x=-4. |
