Теория автоматического управления. Анализ и синтез линейной системы автоматического управления. Пояснительная записка. Введение 4 Лист 4 1 Анализ литературных источников о системах автоматического управления освещенностью помещения 6
 Скачать 1.14 Mb. Скачать 1.14 Mb.
|
2.2 Математическая модель системы автоматизированного управления2.2.1 Дифференциальные уравнения ДПТ НВПри составлении математической модели САУ приниматься следующие допущения: система абсолютно жесткая, то есть двигатель имеет одну степень свободы; масса вращающихся частей постоянна; статический момент, приведенный к валу двигателя, постоянный; реакция якоря скомпенсирована; зависимость угловой скорости вращения вала двигателя от напряжения якоря Uя линейная; поток двигателя неизменен, = const. Далее в таблице 1 приведены характеристики предложенного в техническом задании двигателя постоянного тока независимого возбуждения серии П22. Таблица 1 – Технические характеристики двигателя ДПТ НВ серии П-22У4
Вращающий момент двигателя М расходуется на преодоление динамического момента, обусловленного моментом инерции и статического момента нагрузки Мс. В соответствии со сказанным выше, уравнение моментов имеет следующий вид: 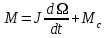 , (1) , (1)где: 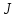 – момент инерции в кг·м²; – момент инерции в кг·м²;М – Движущий момент двигателя в Н·м. Движущий момент двигателя, Н∙м, определяется по формуле: 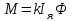 , (2) , (2)где k – конструктивная постоянная двигателя, 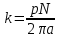 , ,где р – число пар полюсов, N – число активных проводников обмотки якоря, а – число параллельных ветвей. В соответствии с вышесказанным, уравнение моментов может быть представлено в следующем виде: 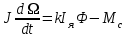 (3) (3)С учетом принятых допущений, уравнение равновесия электрической цепи якоря может быть представлено в следующем виде: 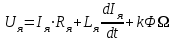 (4) (4)где: Lя – индуктивность цепи якоря, Rя – сопротивление якоря, kФΩ – ЭДС вращения, Uя – напряжение якоря. Преобразовывая уравнение статического равновесия с учетом проведенных выше расчетов, получаем окончательный вид дифференциального уравнение двигателя, записанное относительно регулируемой величины Ω, при входном Uя и возмущающем Мс воздействиях: 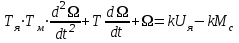 (5) (5)В операторной форме уравнение 4 примет вид: 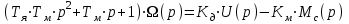 (6) (6)Передаточные функции двигателя по входному и возмущающему воздействиям определяются по формулам 7 и 8 соответственно: 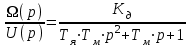 (7) (7)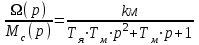 (8) (8)2.2.2 Структурная схема двигателяСистема дифференциальных уравнений двигателя имеет следующий вид: 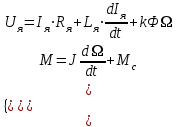 Первое уравнение системы описывает переходные процессы в якорной цепи двигателя. Принимаем за выходную координату ток якоря Ia, за входную – напряжение Ua и противо-ЭДС (Ед=кФΩ). В соответствии с вышесказанным, первое уравнение системы принимает следующий вид: 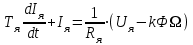 Заменив d/dt на р получим: 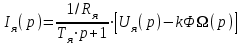 (9) (9)Второе уравнение системы представляют в виде: 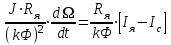 (10) (10)где Ic – статический ток нагрузки, 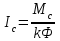 . .В операторной форме уравнение (10) будет иметь вид: 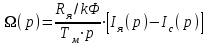 . .С учетом полученных уравнений составляется структурная схема двигателя, представленная на рисунке 12. Р 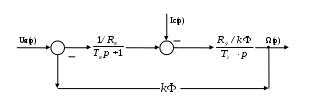 исунок 12 – Структурная схема ДПТ НВ 2.2.3 Расчет параметров двигателяСвязь угловой скорости 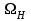 , рад/с., с частотой вращения выражается следующей зависимостью: , рад/с., с частотой вращения выражается следующей зависимостью: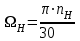 (11) (11)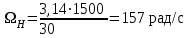 Значение величины k, В∙с, определяется по формуле: 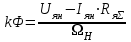 (12) (12)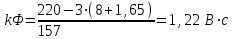 Индуктивность якорной цепи Lя, Гн, определяется по формуле: 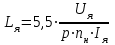 (13) (13) 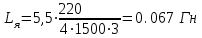 где 5,5 – коэффициент для нескомпенсированных машин. Электромагнитная постоянная времени якорной цепи, 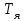 с, определяется по формуле: с, определяется по формуле: 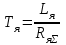 (14) (14)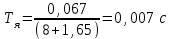 Передаточный коэффициент двигателя по напряжению якоря, рад/(В∙с), определяется по формуле: 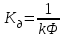 (15) (15)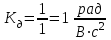 Передаточный коэффициент двигателя по статическому моменту, Ом/(В∙с)2, определяется по формуле: 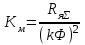 (16) (16)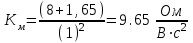 Электромеханическая постоянная времени, 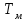 с, определяется по формуле: с, определяется по формуле: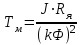 (17) (17)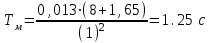 2.2.4 Дифференциальные уравнения тахогенератораУравнение электрического равновесия для цепи возбуждения имеет следующий вид: 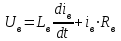 (18) (18)где: Uв – напряжение возбуждения тахогенератора; Lв – индуктивность цепи возбуждения; ів – ток возбуждения; Rв – сопротивление цепи возбуждения. Расчет для якорной цепи: 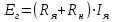 (19) (19)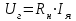 (20) (20)где: Ег – ЭДС тахогенератора, Rя – сопротивление якорной цепи, Rн – сопротивление нагрузки. Преобразовав уравнение ЭДС ТГ получают: 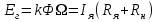 (21) (21)2.2.5 Структурная схема тахогенератораПри составлении передаточной функции тахогенератора, для упрощения расчетов, следует пренебречь: индуктивностью якорной цепи; моментом инерции; реакцией якоря; нелинейностью статической характеристики в зоне малой скорости; пульсациями напряжения; изменением магнитного потока. За выходную координату принимают напряжение Uвых, за входную – скорость Ω: 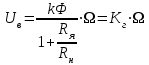 (22) (22)где 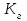 – передаточный коэффициент ТГ, в В·с/рад. – передаточный коэффициент ТГ, в В·с/рад.Передаточная функция тахогенератора имеет следующий вид: 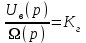 (23) (23)Таким образом, тахогенератор является пропорциональным звеном. Структурная схема тахогенератора представлена на рисунке 13. 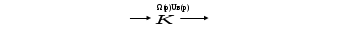 Рисунок 13 – Структурная схема тахогенератора 2.2.6 Передаточная функция операционного усилителяДля получения передаточной функции операционного усилителя используется принципиальная схема, представленная на рисунке 14. ZОС 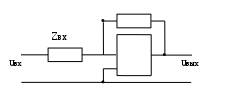 Рисунок 14 – Принципиальная схема операционного усилителя Передаточная функция операционного усилителя относительно одного входа имеет вид: 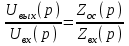 где: Zос(р) – операторное сопротивление обратной связи, Zвх(р) – операторное сопротивление, включенное на вход усилителя. С учетом того, что Zвх = R1, Zoc = R0, получают: 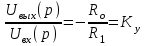 (24) (24)где Ку – коэффициент усиления ОУ. 2.2.7 Коэффициент усиления операционного усилителяКоэффициент усиления разомкнутой системы определяется как произведение коэффициентов усиления всех звеньев, в соответствии с формулой 25: 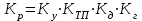 (25) (25)где Ку – коэффициент усиления ОУ, КТП – коэффициент усиления ТП, Кд – коэффициент усиления двигателя, Кг – коэффициент усиления ТГ. С другой стороны, требуемый коэффициент усиления зависит от диапазона регулирования D и точности γ предъявляемой к системе: 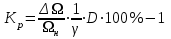 (26) (26)где 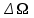 – просадка скорости двигателя при номинальной нагрузке. – просадка скорости двигателя при номинальной нагрузке. Просадка скорости двигателя при номинальной нагрузке определяется: 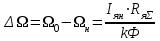 (27) (27)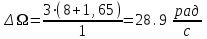 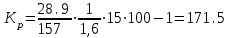 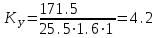 2.2.8 Тиристорный преобразовательСиловая часть преобразователя может рассматриваться как безынерционное звено. С учетом инерционности СИФУ передаточная функция преобразователя для линейного участка его характеристики управления имеет вид: 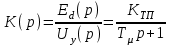 (28) (28)где: Еd – средне выпрямленное значение ЭДС преобразователя, КТП – коэффициент усиления преобразователя, Т – постоянная времени, с учетом постоянных времени операционного усилителя и фильтра. |
