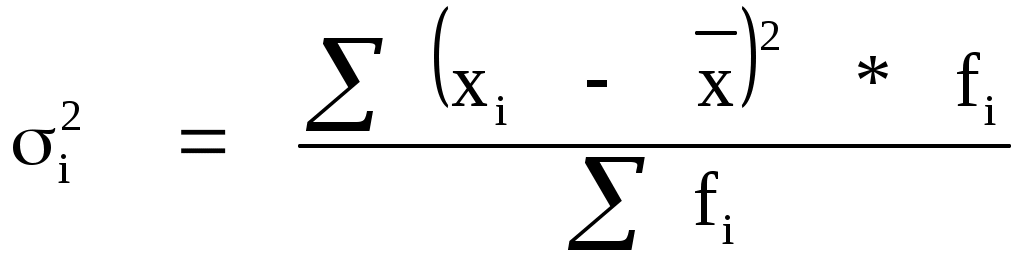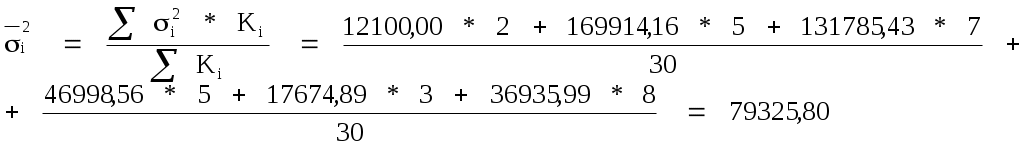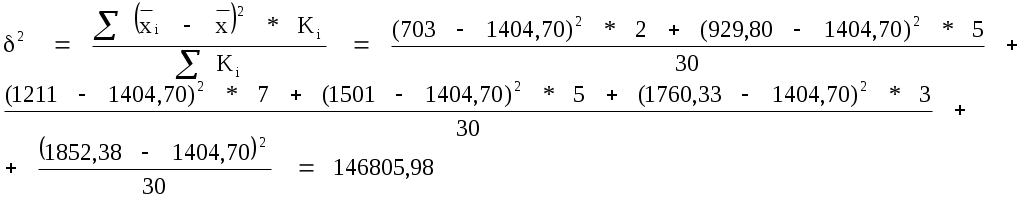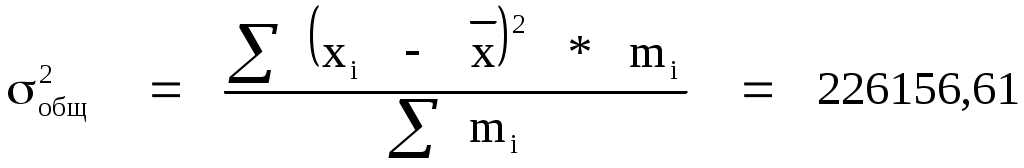Раздел 2.
Ряды распределения
xi
|
500
|
501
|
593
|
813
|
820
|
828
|
832
|
918
|
1100
|
1190
|
1400
|
mi
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
∑ mi
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
|
|
|
|
|
|
|
|
|
|
|
|
xi
|
1410
|
1411
|
1417
|
1584
|
1597
|
1690
|
1700
|
1708
|
1720
|
1735
|
1784
|
mi
|
1
|
1
|
2
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
∑ mi
|
12
|
13
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
|
|
|
|
|
|
|
|
|
|
|
|
xi
|
1792
|
1802
|
1812
|
1905
|
1920
|
1942
|
2300
|
|
|
|
|
mi
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
|
|
|
∑ mi
|
24
|
25
|
26
|
27
|
28
|
29
|
30
|
|
|
|
|
Формула Стерджисса:
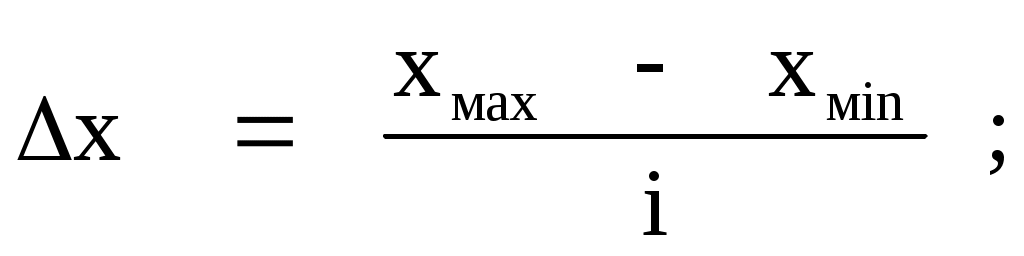 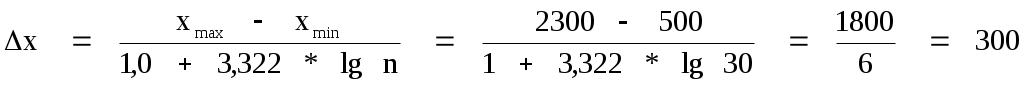

хначi-хконi
|
500,00 - 800,50
|
800,50 – 1101,00
|
1101,00 -1401,50
|
1401,50 -1702,00
|
1702,00 -2002,50
|
2002,50 -2303,00
|
хсрi
|
650,25
|
800,75
|
1251,25
|
1551,75
|
1952,25
|
2152,75
|
mi
|
3
|
6
|
2
|
8
|
10
|
1
|
∑ mi
|
3
|
9
|
11
|
19
|
29
|
30
|
Средняя арифметическая для дискретного ряда
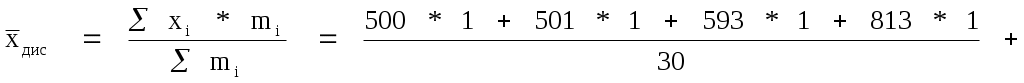
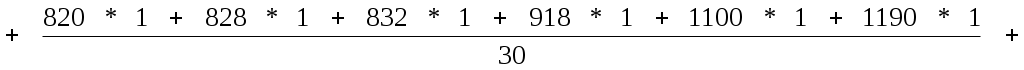
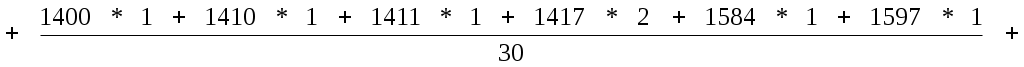
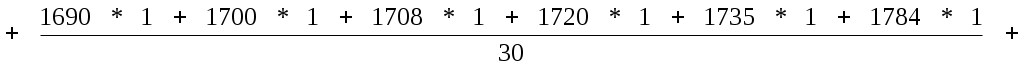
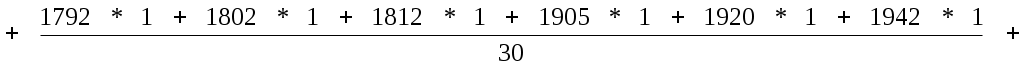
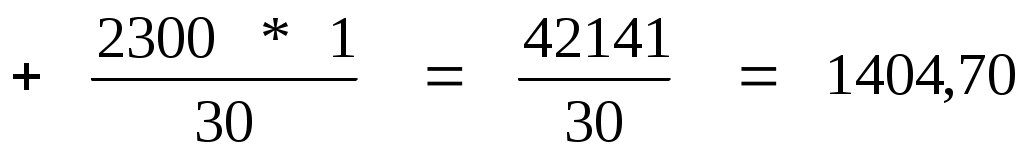
где xi – варианты признака;
mi – соответствующие частоты.
Средняя арифметическая для интервального ряда
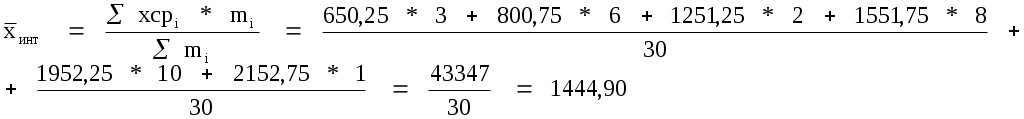
где хсрi – центр i-ого интервала;
mi – частота в i-ом интервале
Мода и медиана
для дискретного ряда
При четном числе вариантов медиана будет равна средней арифметической из двух срединных вариантов.
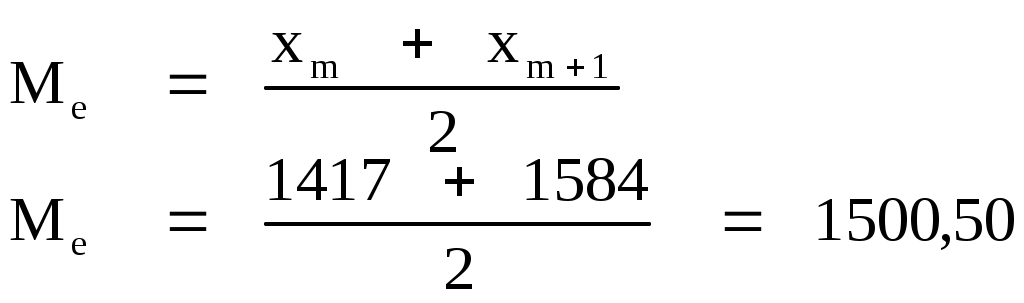
для интервального ряда
Медианным является первый интервал, для которого ∑mi превышает половину от общего числа наблюдений. Т.е. интервал 1401,5 - 1702 – медианный.
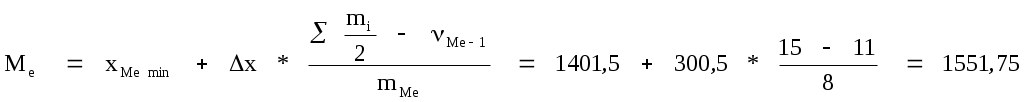
где хМеmin – нижняя граница медианного интервала;
∆х – длина интервала;
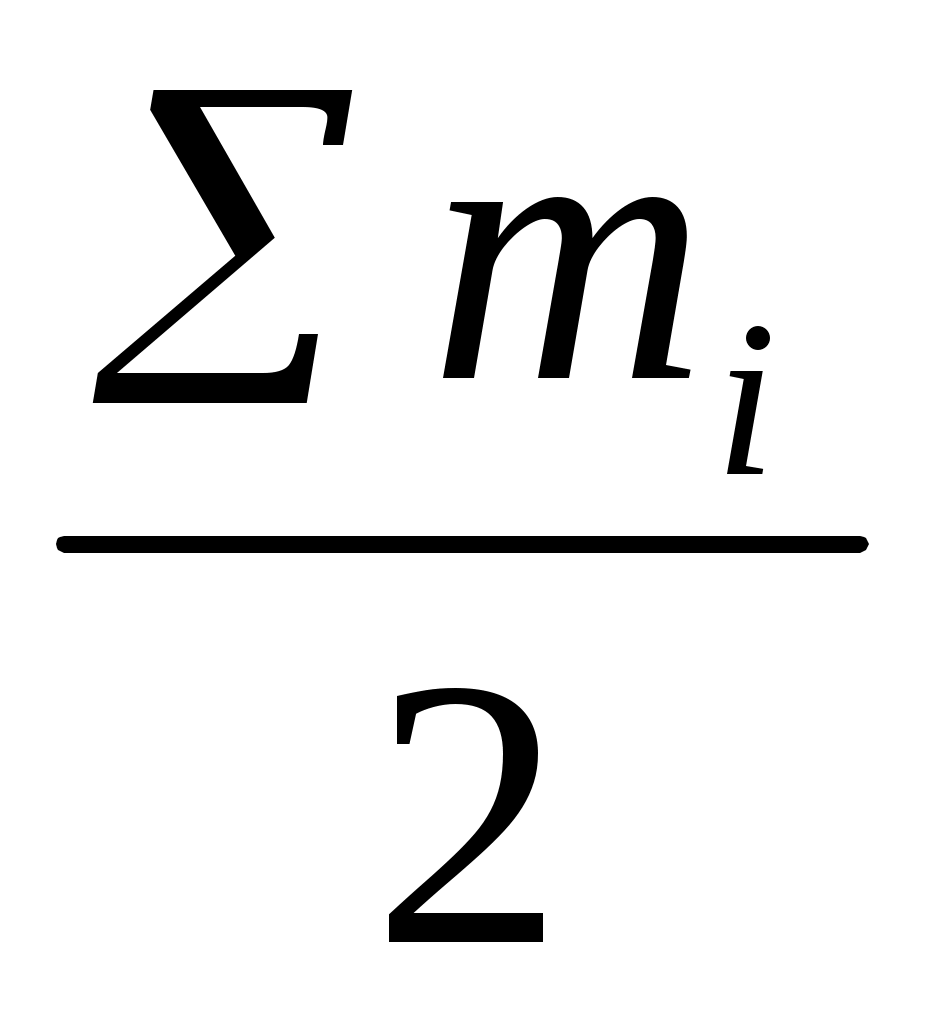 - половина накопленных частот; - половина накопленных частот;
νm-1 – накопленная частота интервалов, предшествующая медианному интервалу
mMe – частота медианного интервала.
Мода - это вариант, наиболее часто встречающийся в данном вариационном ряду.
для дискретного ряда – это вариант с наибольшей частотой.
Мо1 = 1417;
для интервального ряда определяют модальный интервал по наибольшей частоте (mМо = 10)
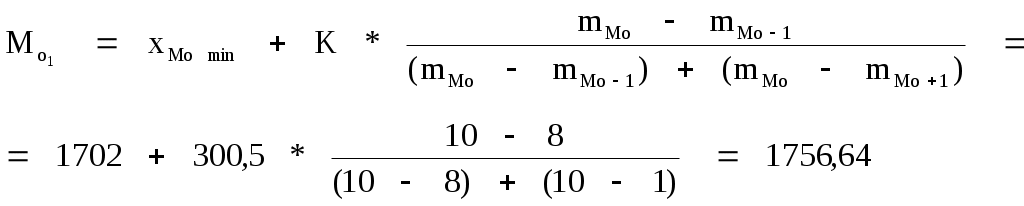
где хМоmin – нижняя граница модального интервала;
К – величина интервала;
mМо – частота интервала;
mMo-1 – частота интервала, предшествующего модальному;
mMo+1 – частота интервала, следующего за модальным.
Показатели вариации
Размах вариации
R = xmax - xmin = 2300-500=1800
2. Среднее линейное отклонение (для интервального ряда).
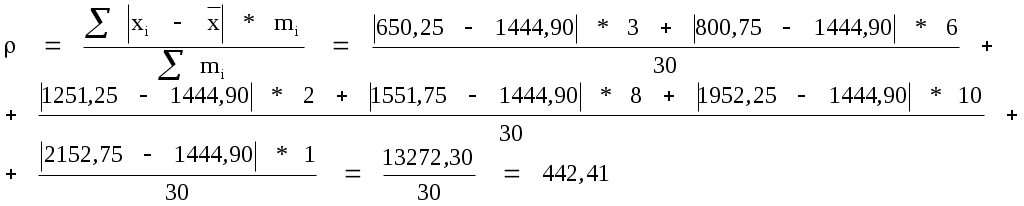
Дисперсия
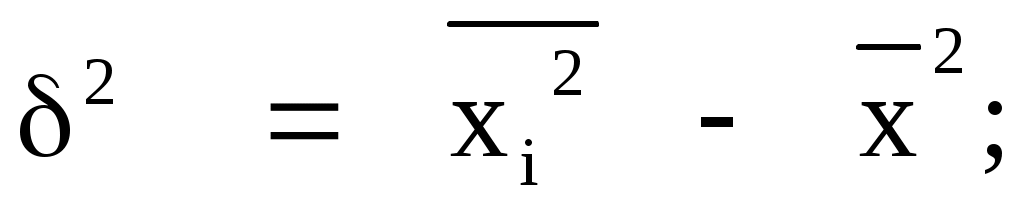
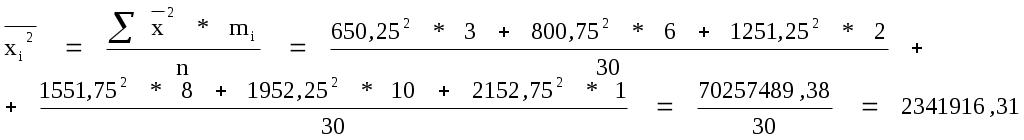
где 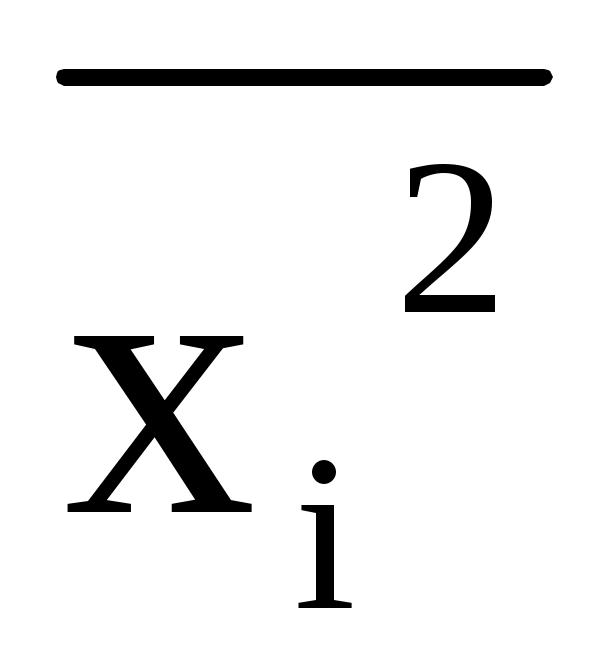 - средняя из квадратов значений признака; - средняя из квадратов значений признака;
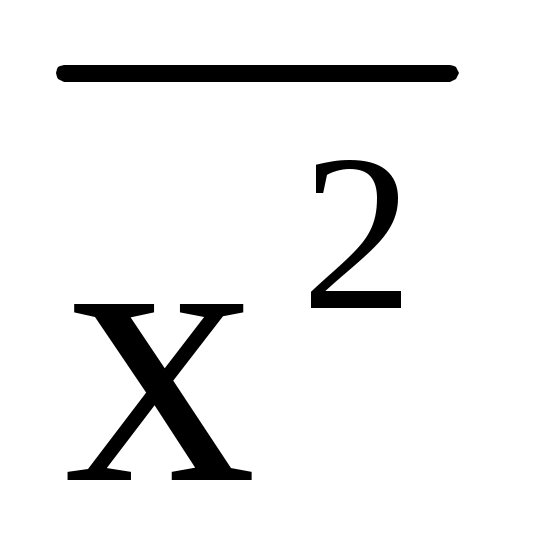 - квадрат средней арифметической; - квадрат средней арифметической;
 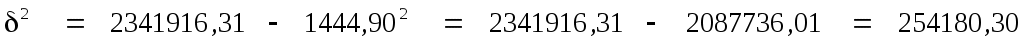
Среднее квадратичное отклонение
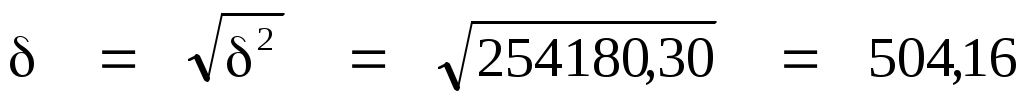
Коэффициенты вариации
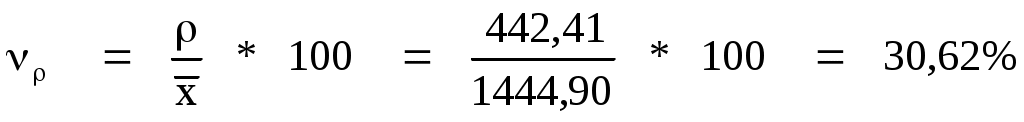
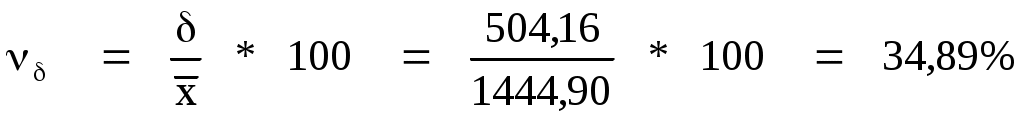
Раздел 3.
Дисперсия. Виды дисперсий
Закон сложения дисперсий
1. Общая дисперсия
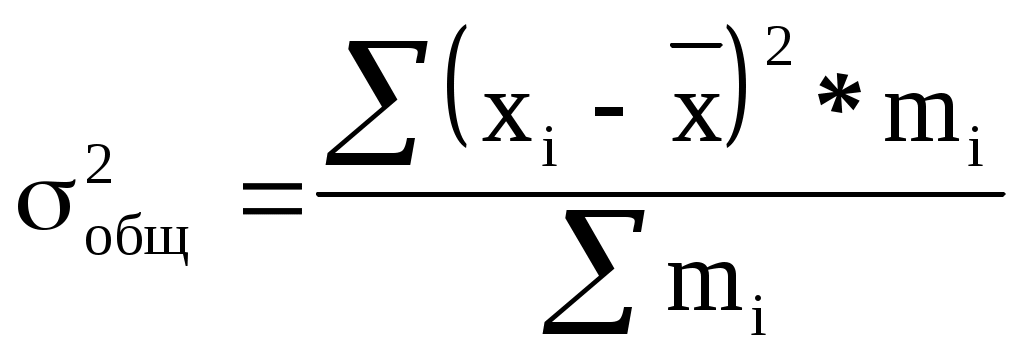 , ,
где 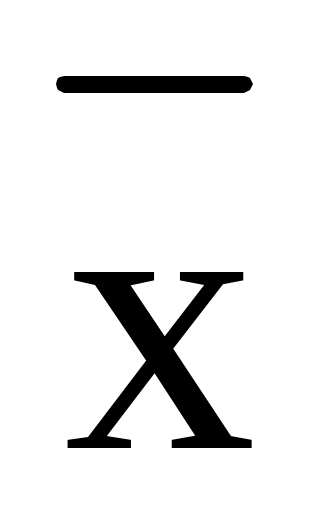 - общая средняя для всей совокупности. - общая средняя для всей совокупности.
xi
|
mi
|
xi*mi
|
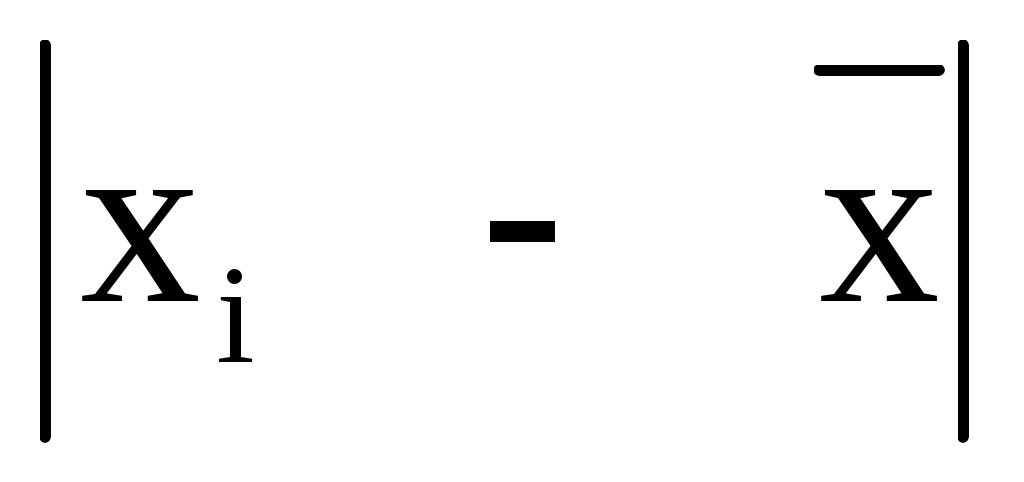
|
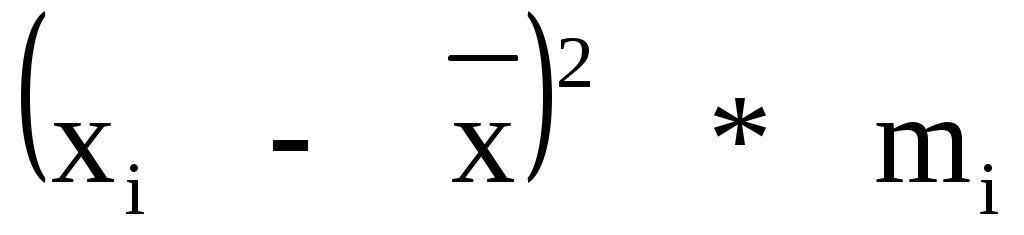
|
500
|
1
|
500
|
904,7
|
818482,09
|
501
|
1
|
501
|
903,7
|
816673,69
|
593
|
1
|
593
|
811,7
|
658856,89
|
813
|
1
|
813
|
591,7
|
350108,89
|
820
|
1
|
820
|
584,7
|
341874,09
|
828
|
1
|
828
|
576,7
|
332582,89
|
832
|
1
|
832
|
572,7
|
327985,29
|
918
|
1
|
918
|
486,7
|
236876,89
|
1100
|
1
|
1100
|
304,7
|
92842,09
|
1190
|
1
|
1190
|
214,7
|
46096,09
|
1400
|
1
|
1400
|
4,7
|
22,09
|
1410
|
1
|
1410
|
5,3
|
28,09
|
1411
|
1
|
1411
|
6,3
|
39,69
|
1417
|
2
|
2834
|
12,3
|
302,58
|
1584
|
1
|
1584
|
179,3
|
32148,49
|
1597
|
1
|
1597
|
192,3
|
36979,29
|
1690
|
1
|
1690
|
285,3
|
81396,09
|
1700
|
1
|
1700
|
295,3
|
87202,09
|
1708
|
1
|
1708
|
303,3
|
91990,89
|
1720
|
1
|
1720
|
315,3
|
99414,09
|
1735
|
1
|
1735
|
330,3
|
109098,09
|
1784
|
1
|
1784
|
379,3
|
143868,49
|
1792
|
1
|
1792
|
387,3
|
150001,29
|
1802
|
1
|
1802
|
397,3
|
157847,29
|
1812
|
1
|
1812
|
407,3
|
165893,29
|
1905
|
1
|
1905
|
500,3
|
250300,09
|
1920
|
1
|
1920
|
515,3
|
265534,09
|
1942
|
1
|
1942
|
537,3
|
288691,29
|
2300
|
1
|
2300
|
895,3
|
801562,09
|
Итого:__3__5281___53024,67'>Итого:__5__7509___234992,80'>Итого:__7__8477___922498,00'>Итого:__5__4649___849570,80'>Итого:__2__1406___24200,00'>Итого:__30__42141____6784698,30'>Итого:
|
30
|
42141
|
|
6784698,30
|
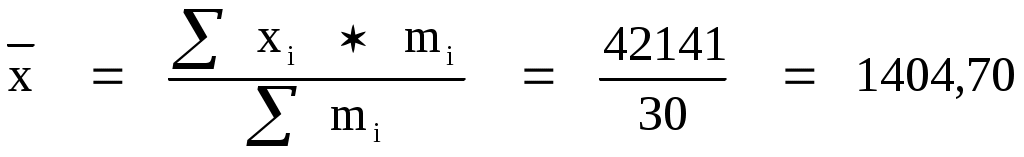
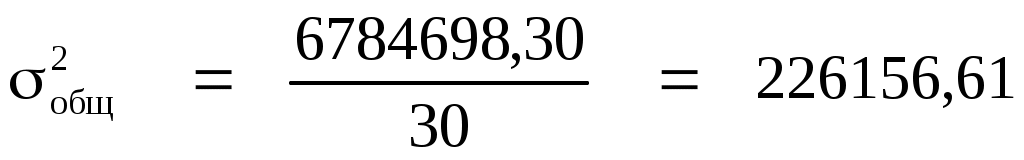
Внутригрупповая дисперсия
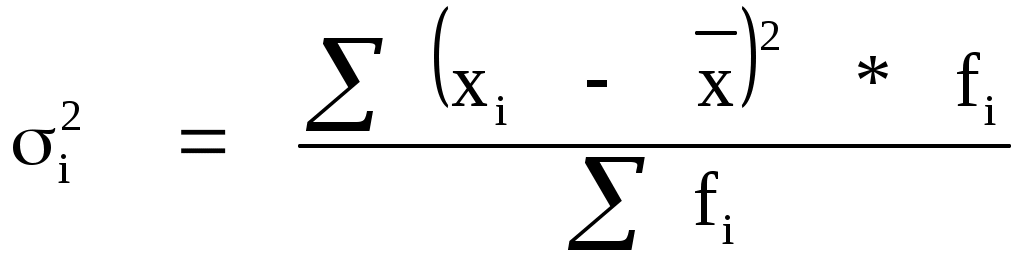
где 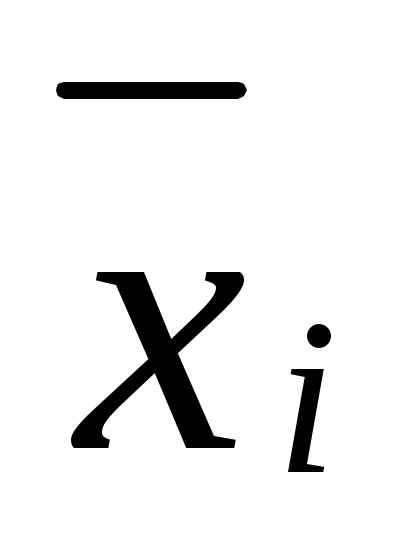 - среднее значение признака в i-й группе; - среднее значение признака в i-й группе;
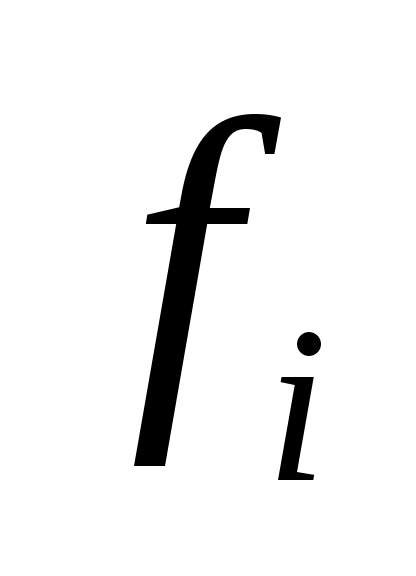 - повторяемость отдельных значений признака в i-й группе. - повторяемость отдельных значений признака в i-й группе.
1 группа
xi
|
fi
|
xi * fi
|
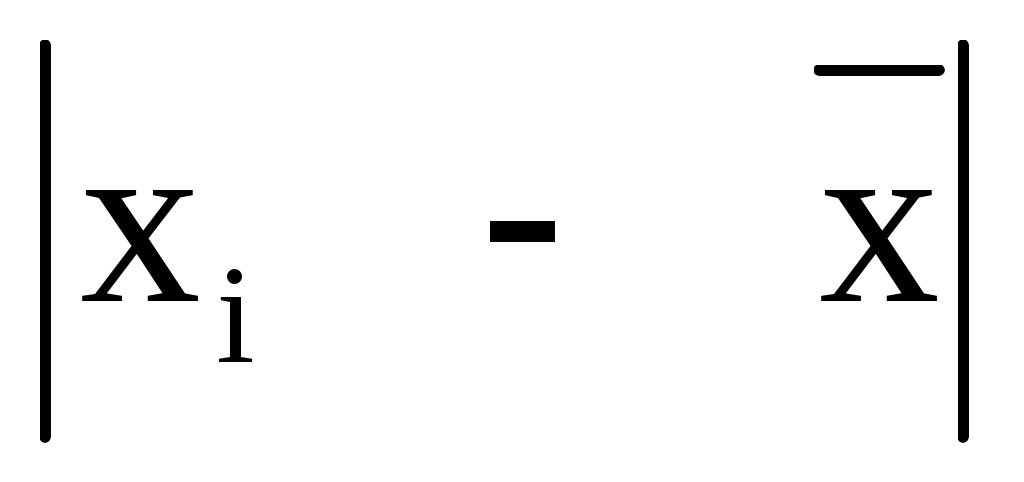
|
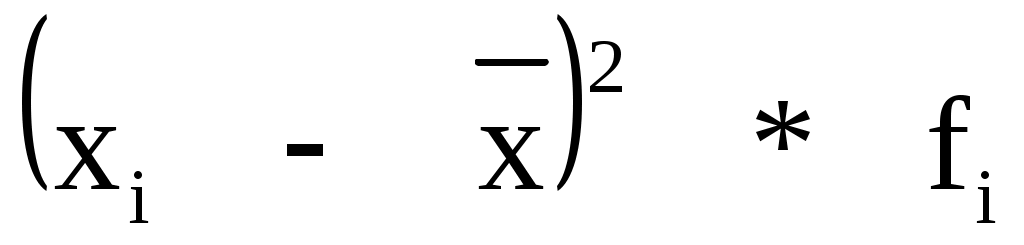
|
593
|
1
|
593
|
110
|
12100,00
|
813
|
1
|
813
|
110
|
12100,00
|
Итого:
|
2
|
1406
|
|
24200,00
|
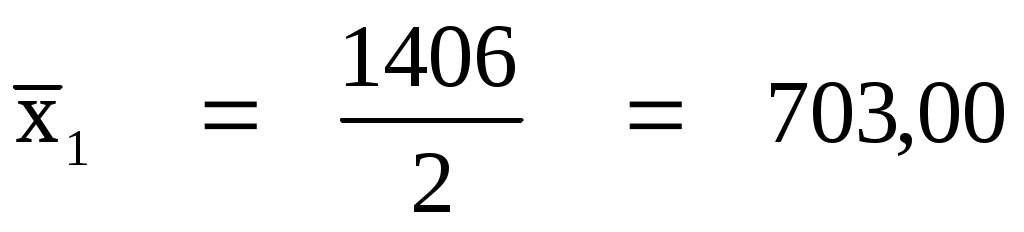
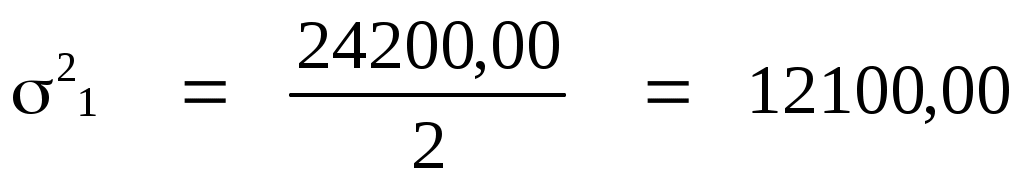
2 группа
xi
|
fi
|
xi * fi
|
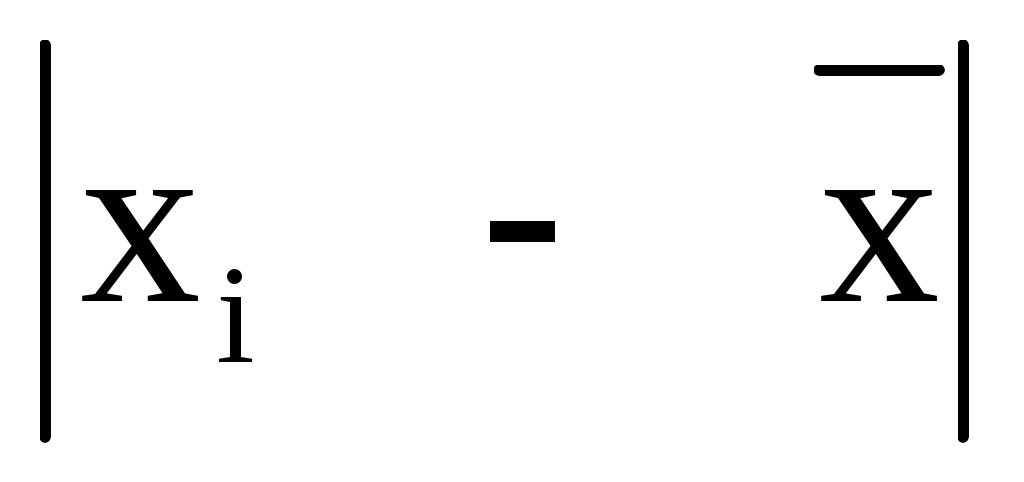
|
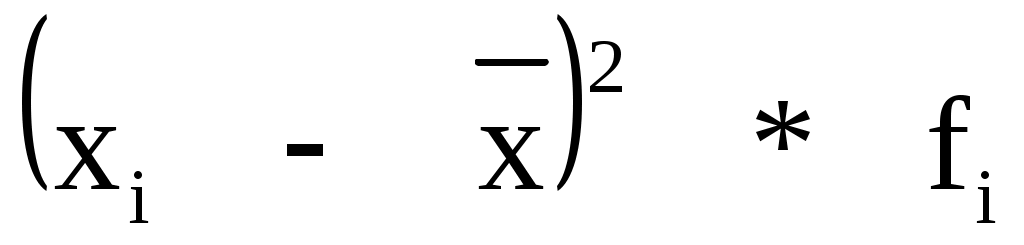
|
500
|
1
|
500
|
429,80
|
184728,04
|
501
|
1
|
501
|
428,80
|
183869,44
|
820
|
1
|
820
|
109,80
|
12056,04
|
1411
|
1
|
1411
|
481,20
|
231553,44
|
1417
|
1
|
1417
|
487,20
|
237363,84
|
Итого:
|
5
|
4649
|
|
849570,80
|
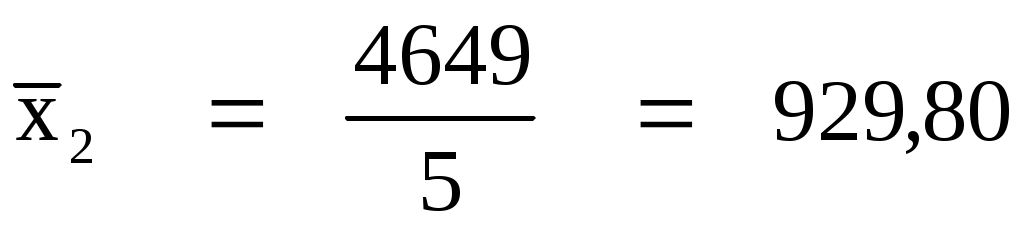
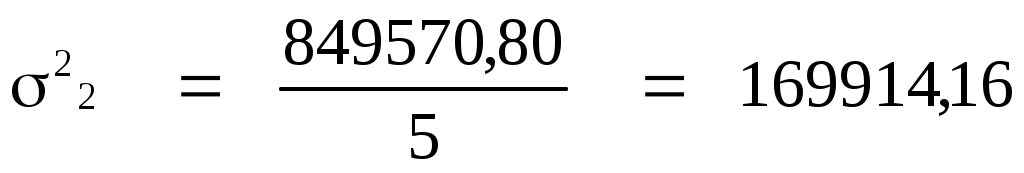
3 группа
xi
|
fi
|
xi * fi
|
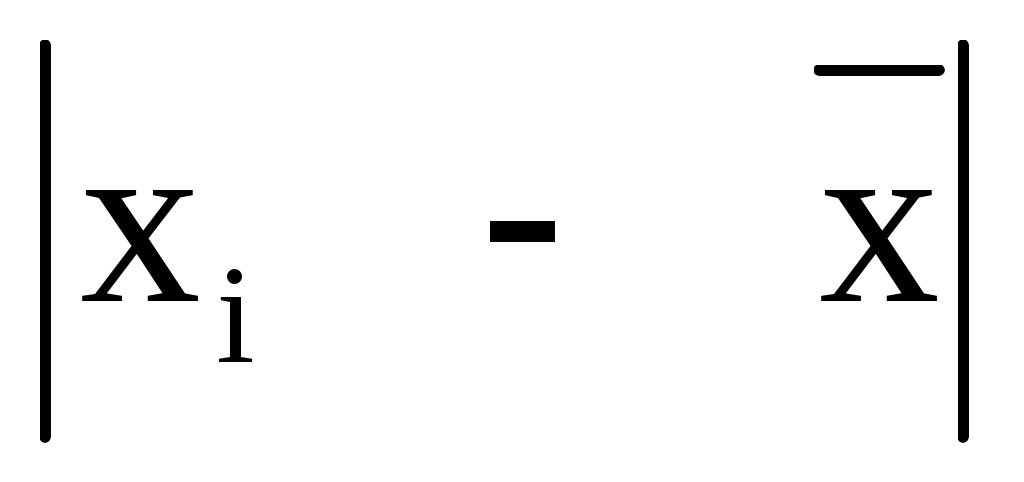
|
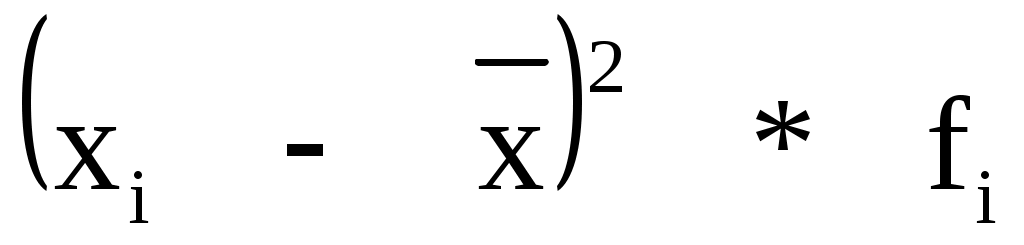
|
828
|
1
|
828
|
383,00
|
146689,00
|
832
|
1
|
832
|
379,00
|
143641,00
|
918
|
1
|
918
|
293,00
|
85849,00
|
1100
|
1
|
1100
|
111,00
|
12321,00
|
1400
|
1
|
1400
|
189,00
|
35721,00
|
1597
|
1
|
1597
|
386,00
|
148996,00
|
1802
|
1
|
1802
|
591,00
|
349281,00
|
Итого:
|
7
|
8477
|
|
922498,00
|
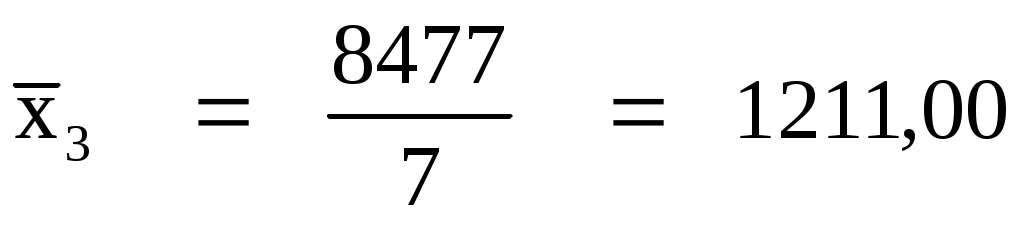
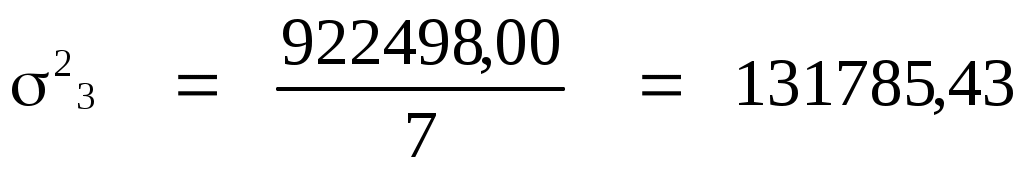
4 группа
xi
|
fi
|
xi * fi
|
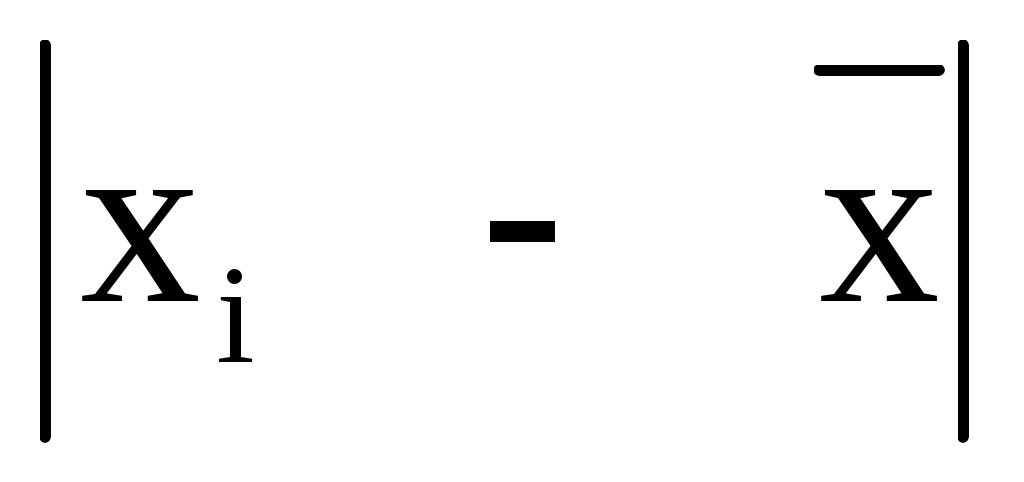
|
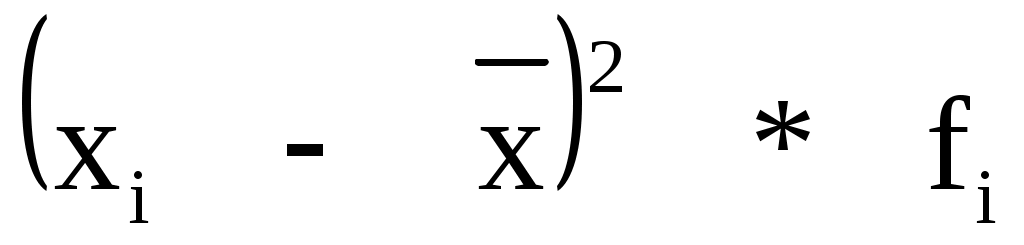
|
1190
|
1
|
1190
|
311,80
|
97219,24
|
1410
|
1
|
1410
|
91,80
|
8427,24
|
1417
|
1
|
1417
|
84,80
|
7191,04
|
1708
|
1
|
1708
|
206,20
|
42518,44
|
1784
|
1
|
1784
|
282,20
|
79636,84
|
Итого:
|
5
|
7509
|
|
234992,80
|
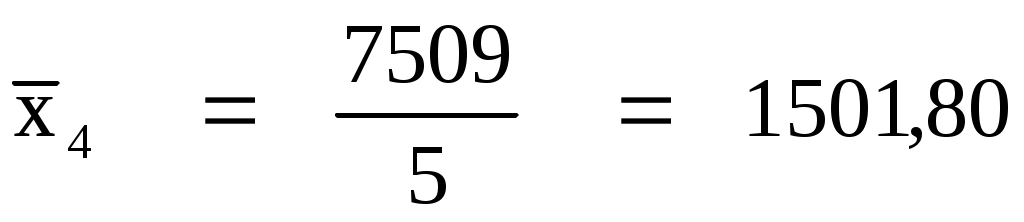
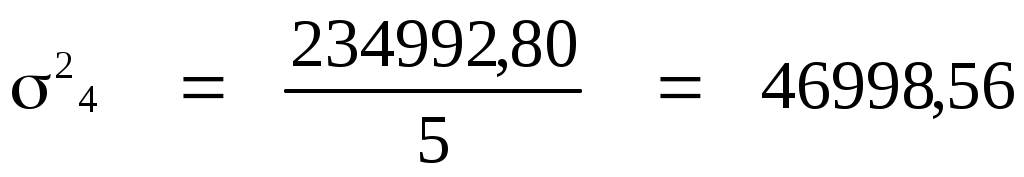
5 группа
xi
|
fi
|
xi * fi
|
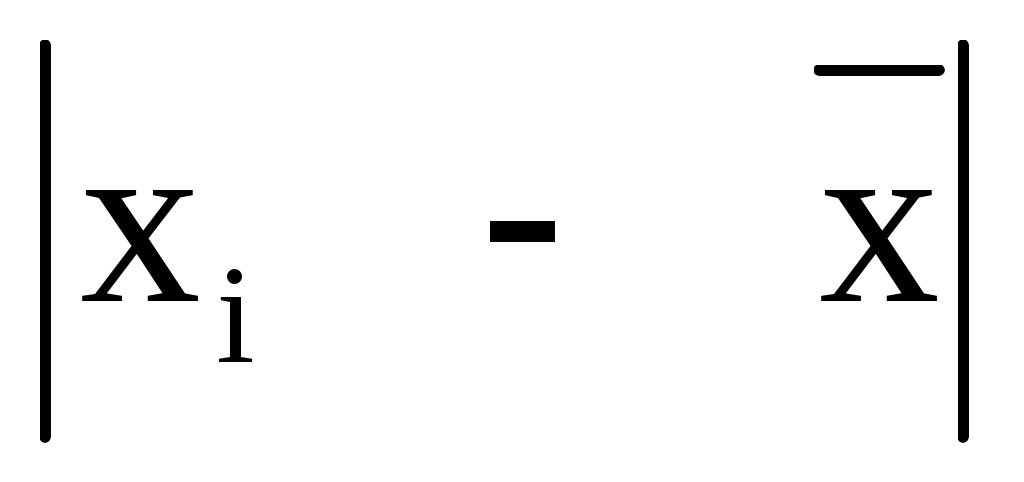
|
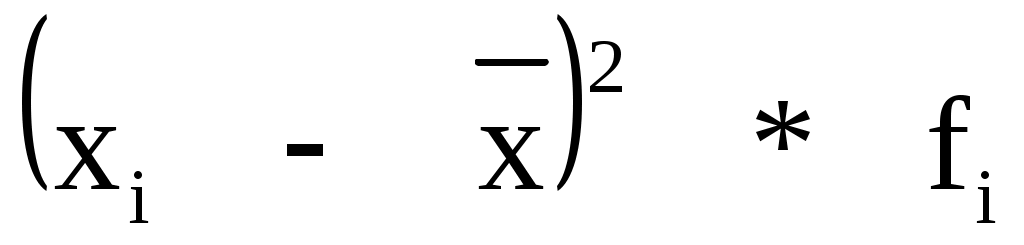
|
1584
|
1
|
1584
|
176,33
|
31092,27
|
1792
|
1
|
1792
|
31,67
|
1002,99
|
1905
|
1
|
1905
|
144,67
|
20929,41
|
Итого:
|
3
|
5281
|
|
53024,67
|
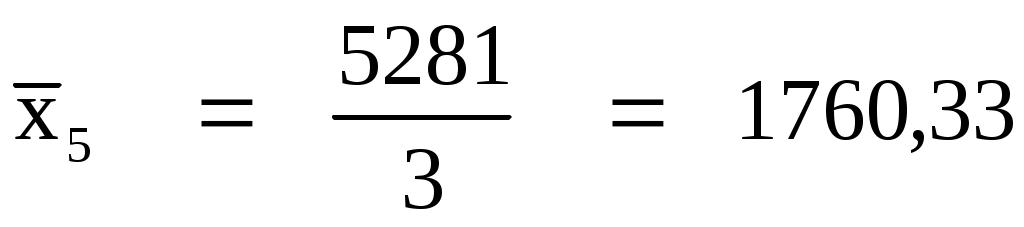
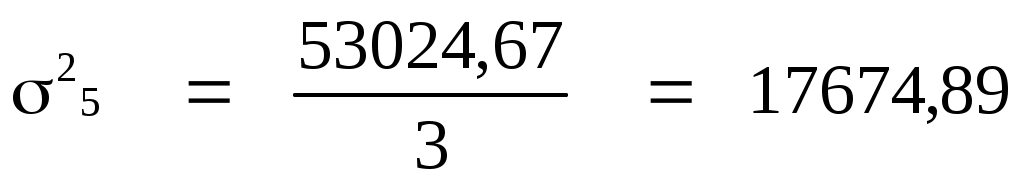
6 группа
xi
|
fi
|
xi * fi
|
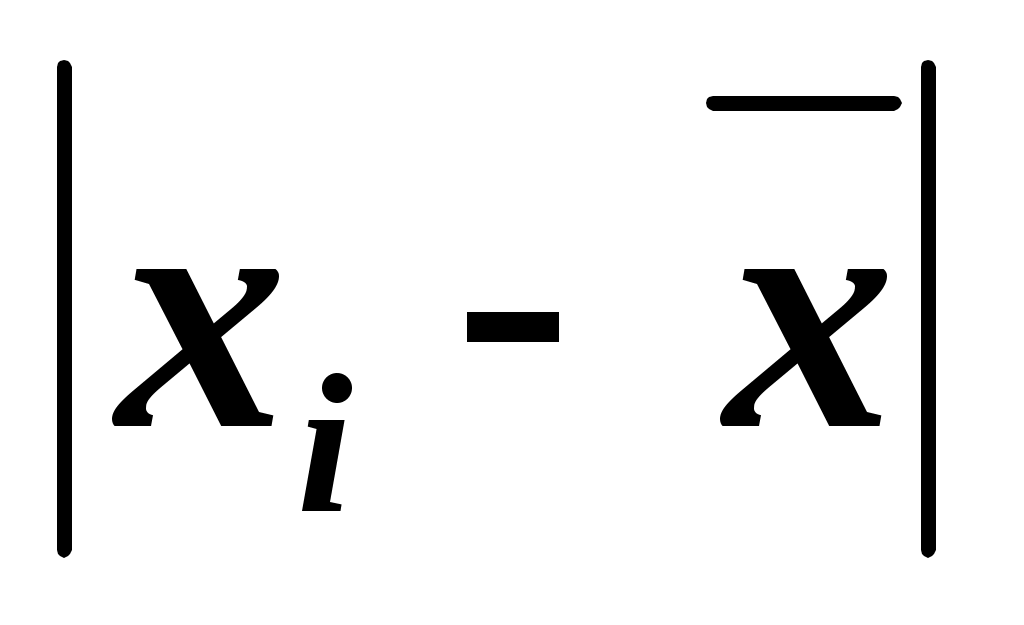
|
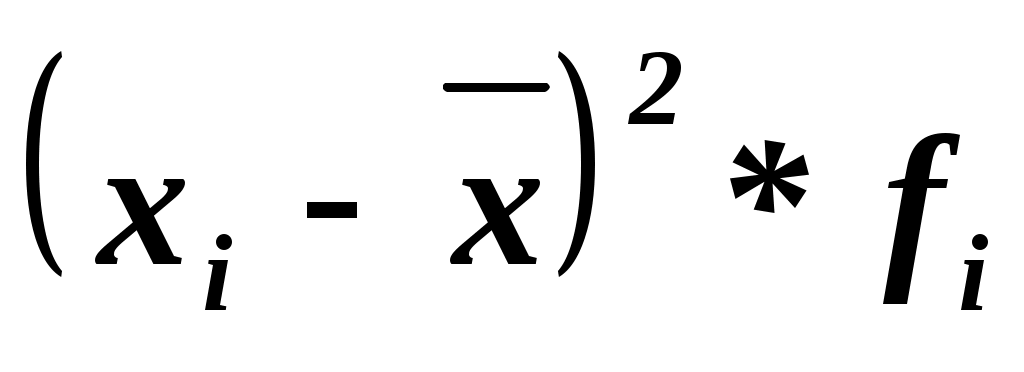
|
1690
|
1
|
1690
|
162,38
|
26367,26
|
1700
|
1
|
1700
|
152,38
|
23219,66
|
1720
|
1
|
1720
|
132,38
|
17524,46
|
1735
|
1
|
1735
|
117,38
|
13778,06
|
1812
|
1
|
1812
|
40,38
|
1630,54
|
1920
|
1
|
1920
|
67,62
|
4572,46
|
1942
|
1
|
1942
|
89,62
|
8031,74
|
2300
|
1
|
2300
|
447,62
|
200363,66
|
Итого:
|
8
|
14819
|
|
295487,88
|
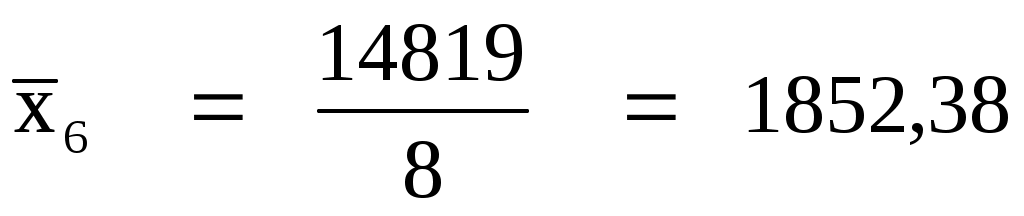
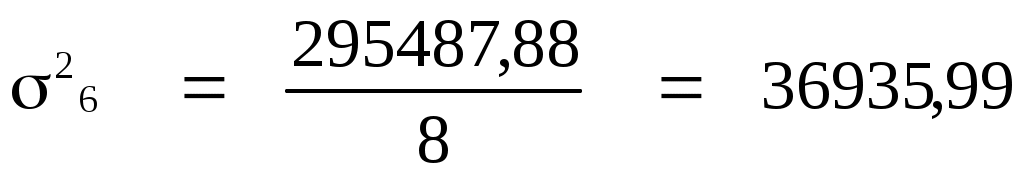
Средняя из внутригрупповых дисперсий
Средняя из внутригрупповых дисперсий рассчитывается как средняя арифметическая, взвешенная по численности отдельных групп:
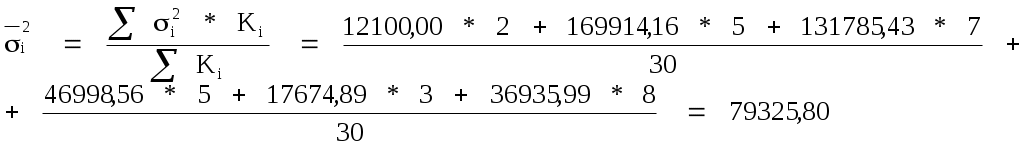
где 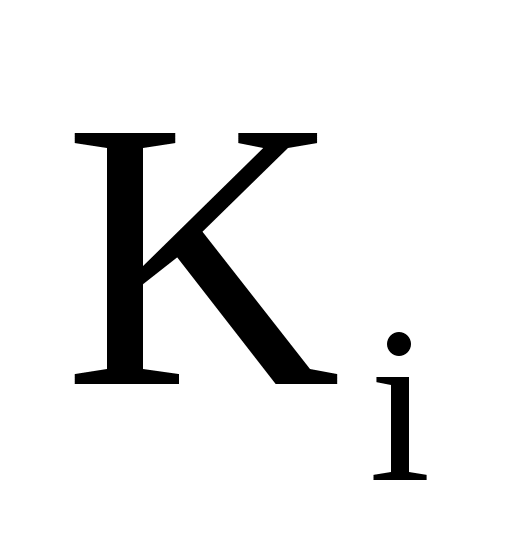 - абсолютный или относительный вес i-й группы в общей совокупности. - абсолютный или относительный вес i-й группы в общей совокупности.
Межгрупповая дисперсия
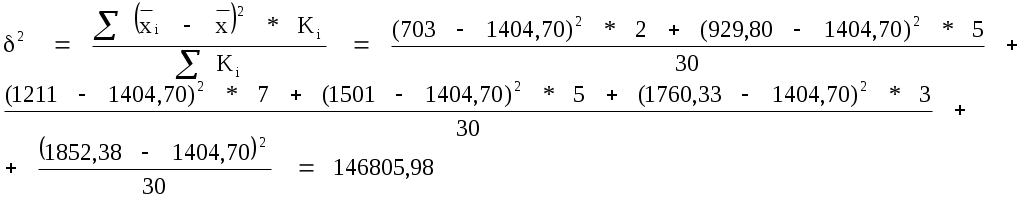
Закон сложения дисперсий
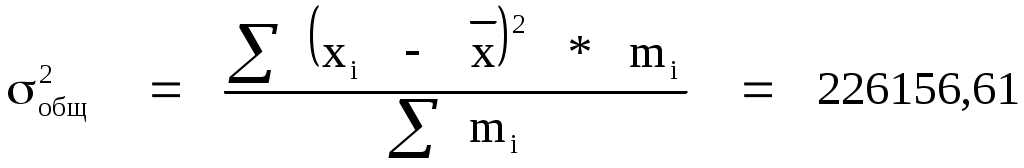
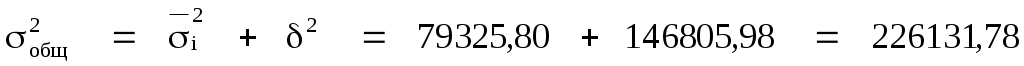
Коэффициент детерминации (корреляционное отношение)
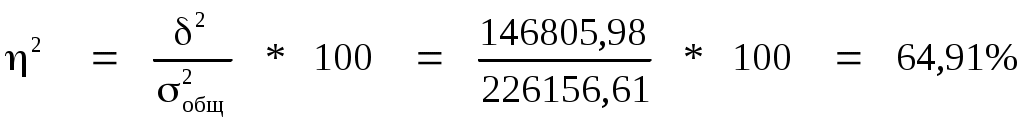
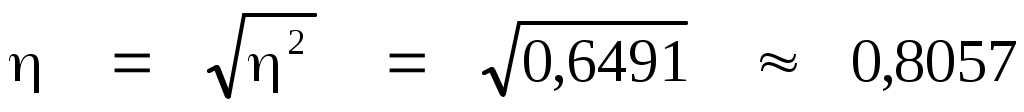
|
 Скачать 0.91 Mb.
Скачать 0.91 Mb.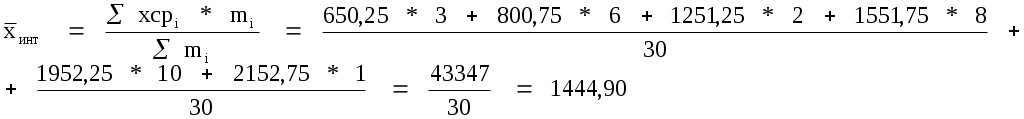
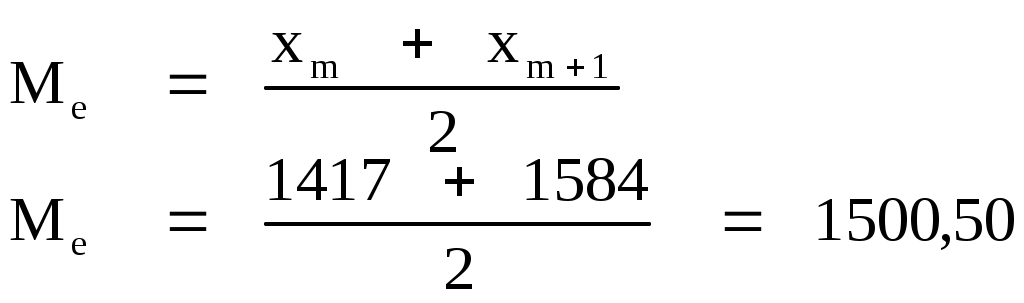
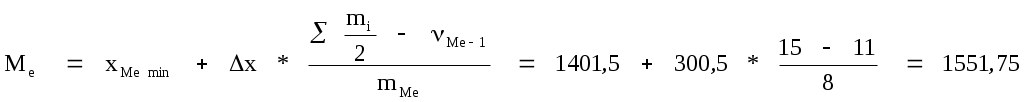
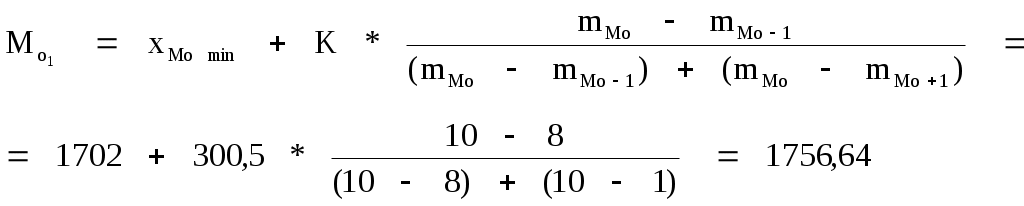
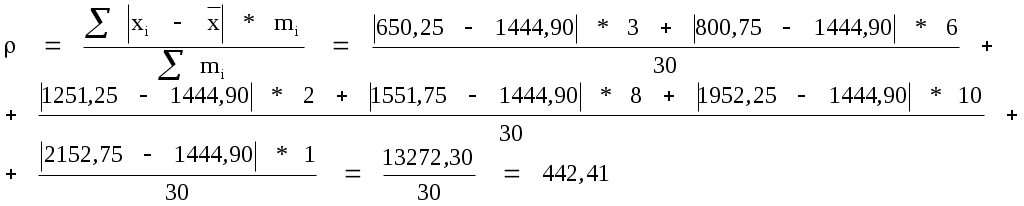
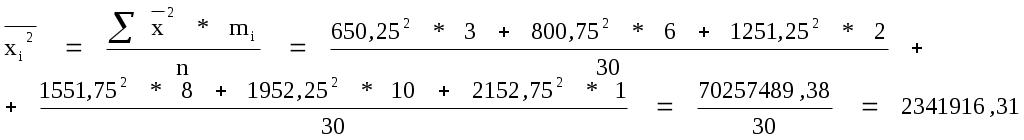
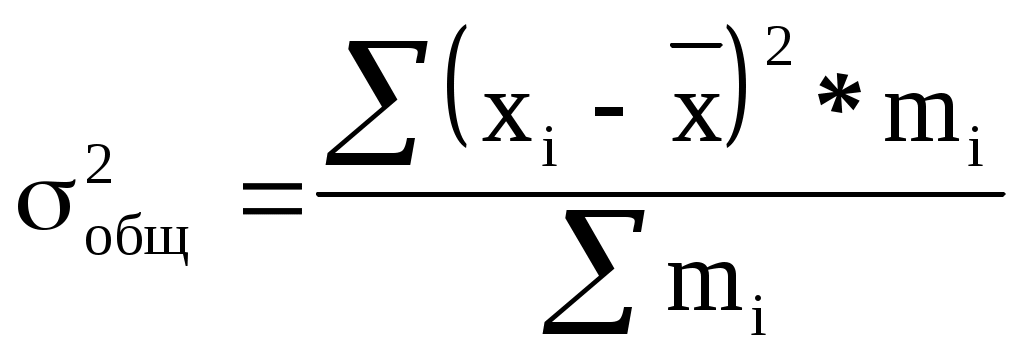 ,
,