Гидравлика. Введение гидравлика относится к числу древнейших наук
 Скачать 5.48 Mb. Скачать 5.48 Mb.
|
|
ВВЕДЕНИЕ Гидравлика относится к числу древнейших наук. Первые гидравлические системы водоснабжения и ирригации были известны человеку еще задолго до нашей эры. Уже в Древнем Египте, Индии и Китае, странах Ближнего Востока умели строить на реках плотины и водяные мельницы, оросительные системы на рисовых полях, в которых использовались водоподъемные машины. В Риме за шесть столетий до нашей эры был построен водопровод, что свидетельствует о высокой технической культуре того времени. В III веке до нашей эры Архимед изобрел машину для подъема воды, названную «архимедовым винтом» и являющуюся прообразом современных гидравлических насосов. По мере развития науки и техники совершенствовались гидравлические и пневматические системы, и существенно расширялась сфера их практического применения. В настоящее время гидравлические машины, гидро- и пневмоприводы широко используют в водоснабжении и мелиорации, машиностроении и металлургии, на всех видах транспорта и в строительстве. Важную роль в развитии современной техники играют гидравлические и пневматические приводы как основное средство механизации и автоматизации технологических процессов и процессов управления различными объектами. В качестве исполнительных устройств такие приводы применяют в станках и автоматических линиях, роботах и манипуляторах, системах управления автомобилем, самолетом и т.п. Очевидно, что техническое совершенствование гидравлических и пневматических систем не могло происходить без фундаментальных научных разработок, начало которым положил трактат Архимеда «О плавании тел». В XV—XVII веках в трудах Леонардо да Винчи, Г. Галилея, И. Ньютона были сформулированы отдельные законы равновесия и движения жидкости, а в середине XVIII века Д. Бернулли и Л. Эйлер заложили теоретические основы гидромеханики как науки. В XIX—XX веках гидромеханика получила дальнейшее развитие в трудах Дж. Г. Стокса, О. Рейнольдса, Н. Е. Жуковского, Н. П. Петрова, Л. Прандтля и других ученых. Этот период характеризуется бурным развитием науки и техники, поэтому в трудах по гидромеханике большое внимание уделяется вопросам, представляющим практический интерес. Формируется раздел гидромеханики, рассматривающий законы равновесия и движения жидкости в открытых и закрытых руслах и способы их применения для решения технических задач. Этот раздел гидромеханики получил название «гидравлика». Именно гидравлика как прикладная наука совместно с газовой динамикой, изучающей законы движения газа, является научной основой для расчета и проектирования современных гидравлических и пневматических систем и их элементов. В настоящем учебном пособии рассматриваются основные законы гидравлики, и описывается работа различных гидравлических и пневматических устройств, принцип действия которых основан на этих законах. Освещаются методы построения гидравлических и пневматических систем на базе этих устройств. Даются методы расчета основных параметров трубопроводов, гидравлических и пневматических машин, элементов управления и контроля гидравлических и пневматических приводов. ЧАСТЬ I. ОСНОВЫ ГИДРАВЛИКИ 1 ОБЩИЕ ПОЛОЖЕНИЯ1.1 Предмет гидравлики, основные понятия и определения Раздел механики, в котором изучаются равновесие и движение жидкостей, а также взаимодействие между жидкостью и обтекаемыми ею поверхностями или телами, называется «механика жидкости», или «гидромеханика». Термин «жидкость» в гидромеханике обладает более широким значением, чем это принято в современном русском языке. В понятие «жидкость» включают физические тела, обладающие текучестью, то есть способностью изменять свою форму под воздействием сколь угодно малых сил. Поэтому под этим термином подразумеваются не только обычные (капельные) жидкости, но и газы. Несмотря на их различие, законы движения капельных жидкостей и газов при определенных условиях можно считать одинаковыми. Основным из этих условий является небольшое значение скорости движения по сравнению со скоростью звука. Одним из прикладных разделов гидромеханики является гидравлика, которая решает определенный круг технических задач и вопросов. Прикладной характер этого раздела подчеркивает само слово «гидравлика», которое образовано из греческих слов hydor — вода и aulos — трубка. Поэтому гидравлика рассматривается как наука о законах равновесия и движения жидкостей и о способах приложения этих законов для решения практических задач. Гидравлика изучает в первую очередь течения жидкостей в различных руслах, т.е. потоки, ограниченные стенками. В понятие «русло» мы будем включать все устройства, ограничивающие поток, в том числе трубопроводы, проточные части насосов, зазоры и другие элементы гидравлических систем. Таким образом, в гидравлике изучаются в основном внутренние течения и решаются «внутренние» задачи. Внешние течения, связанные с обтеканием движущихся тел воздушной или жидкой средой, рассматриваются в аэрогидромеханике, которая в настоящее время получила также значительное развитие в связи с потребностями авиации, авто- и судостроения. Аэрогидромеханика, являющаяся весьма обширной областью исследований и практического применения, не менее важна, однако в данном учебном пособии она не рассматривается. Современная гидравлика является результатом развития двух методов исследования и решения технических задач. Первый из этих методов — теоретический, основанный на использовании законов механики. Развитие его привело к созданию математического описания практически всех основных процессов, происходящих в движущейся жидкости. Однако использование этих математических моделей не всегда позволяет решать практические задачи. Это связано, с одной стороны, со сложностью используемых математических зависимостей, а с другой стороны, — с необходимостью учета влияния большого числа конструктивных факторов. Второй метод — экспериментальный, учитывающий практическую деятельность людей, в результате которой накоплен значительный опыт по созданию гидравлических систем. Современные способы решения прикладных задач, применяемые в гидравлике, представляют собой комбинацию отмеченных методов. Суть их заключается в следующем: сначала исследуемое явление упрощается (вводятся разумные допущения), а затем к нему применяют теоретические методы гидромеханики и на их основе получают расчетные формулы. По формулам проводят необходимые вычисления, и полученные результаты сравнивают с опытными данными. На основе сравнения расчетные зависимости рекомендуют к применению на практике или вносят в них необходимые коррективы. Таким образом, методы, применяемые в гидравлике, являются сочетанием аналитических и экспериментальных способов исследования. 1.2 Силы, действующие в жидкости. Давление Жидкость в гидравлике рассматривают как сплошную среду без пустот и промежутков. Кроме того, не учитывают влияние отдельных молекул, то есть даже бесконечно малые частицы жидкости считают состоящими из весьма большого количества молекул. Из курса физики известно, что вследствие текучести жидкости, т. е. подвижности ее частиц, она не воспринимает сосредоточенные силы. Поэтому в жидкости действуют только распределенные силы, причем эти силы могут распределяться по объему жидкости или по поверхности. Первые называются массовыми, или объемными, а вторые — поверхностными. К объемным (массовым) силам относятся силы тяжести и силы инерции. Они пропорциональны массе и подчиняются второму закону Ньютона. К поверхностным силам следует отнести силы, с которыми воздействуют на жидкость соседние объемы жидкости или тела, так как это воздействие осуществляется через поверхности. Учитывая важность поверхностных сил в гидравлике, рассмотрим их подробнее. Пусть на плоскую поверхность площадью Sпод произвольным углом действует сила R(рисунок 1.1). Силу Rможно разложить на тангенциальную Т инормальную F составляющие. Т  ангенциальная составляющая называется силой трения Т и вызывает в жидкости касательные напряжения (или напряжения трения): ангенциальная составляющая называется силой трения Т и вызывает в жидкости касательные напряжения (или напряжения трения): Единицей измерения касательных напряжений в системе СИ является Паскаль (Па) — ньютон, отнесенный к квадратному метру (1 Па = 1 Н/м2). Нормальная сила Fназывается силой давления и вызывает в жидкости нормальные напряжения сжатия, которые определяются отношением p = F/S. (1.1) Нормальные напряжения, возникающие в жидкости под действием внешних сил, называются гидромеханическим давлением или просто давлением. Рассмотрим системы отсчета давления и единицы его измерения. Важным при решении практических задач является выбор системы отсчета давления (шкалы давления). За начало шкалы может быть принят абсолютный нуль давления. При отсчете давлений от этого нуля их называют абсолютными рабс(рисунок 1.2, а). Однако, как показывает практика, технические задачи удобнее решать, используя избыточные давления ризб, т.е. когда за начало шкалы принимается атмосферное давление (см. рисунок 1.2, а). Давление, которое отсчитывается «вниз» от атмосферного нуля, называется давлением вакуума рвак ,, или вакуумом (см. рисунок 1.2, а). Таким образом, существуют три шкалы для отсчета давления, то есть давление может быть абсолютным, избыточным или вакуумным. Получим формулы для пересчета одного давления в другое. Для получения формулы пересчета избыточного давления в абсолютное рабсвоспользуемся рисунком 1.2, б. Пусть значение искомого давления определяется положением точки В. Тогда очевидно, что рабе = ра + ризб, (1.2) где ра — атмосферное давление, измеренное барометром Связь между абсолютным давлением рабе и давлением вакуума рвакможно установить аналогичным путем, но уже исходя из положения точки С (рис. 1.2, в): рабе = ра - рвак(1.3) И избыточное давление, и вакуум отсчитываются от одного нуля (0атм), но в разные стороны. Следовательно, ризб, = - рвак. (1.4) Таким образом, формулы (1.2)...(1.4) связывают абсолютное, избыточное и вакуумное давления и позволяют пересчитать одно в другое. Практика показала, что для решения технических (прикладных) задач наиболее удобно использовать избыточные давления. Основной единицей измерения давления в системе СИ является паскаль (Па), который равен давлению, возникающему при действии силы в 1 Н на площадь размером 1 м2 (1 Па = 1 Н/м2). 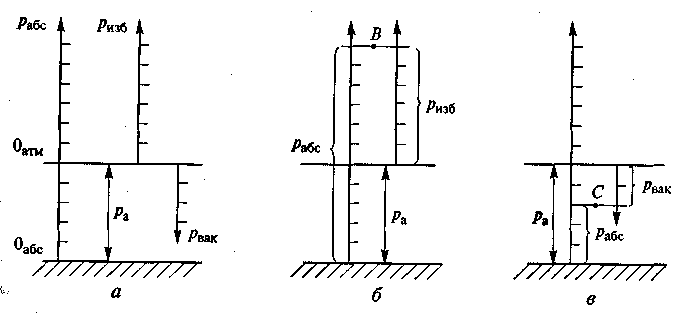 a — шкалы давления; б — взаимосвязь абсолютного и избыточного давлений; в — взаимосвязь абсолютного давления и давления вакуума Рисунок 1.2 - Системы отсчета давления Однако чаще используются более крупные единицы: килопаскаль (1 кПа = 103 Па) и мегапаскаль (1 МПа = 106 Па). В технике широкое распространение получила внесистемная единица - техническая атмосфера (ат), которая равна давлению, возникающему при действии силы в 1 кгс на площадь размером 1 см2 (1 ат = 1 кгс/см2). Соотношения между наиболее используемыми единицами следующие: 10 ат = 0,981 МПа ≈ 1 МПа или 1 ат = 98,1 кПа ≈ 100 кПа. В зарубежной литературе используется также единица измерения давления бар (1 бар = 105 Па). 1.3 Основные физические свойства жидкостей и газов Рассмотрим некоторые свойства жидкостей, которые оказывают наиболее существенное влияние на происходящие в них процессы и поэтому учитываются при расчетах гидравлических систем. 1.3.1 Плотность и удельный вес Важнейшими характеристиками механических свойств жидкости являются ее плотность и удельный вес. Они определяют «весомость» жидкости. Под плотностью ρ (кг/м3) понимают массу жидкости т, заключенную в единице ее объема V, т.е. ρ = m/V. Вместо плотности в формулах может быть использован также удельный вес γ (Н/м3), т.е. вес G, приходящийся на единицу объема V: γ =G/V. Плотность и удельный вес жидкости связаны между собой. Эта связь легко устанавливается, если учесть, что G = mg: γ =G/V = mg/V = ρ g . Изменения плотности и удельного веса жидкости при изменении температуры и давления незначительны, и в большинстве случаев их не учитывают. Плотности наиболее употребляемых жидкостей и газов (кг/м3): бензин — 710...780; керосин — 790...860; вода — 1000; ртуть — 13600; масло гидросистем (АМГ-10) — 850; масло веретенное — 890...900; масло индустриальное — 880...920; масло турбинное — 900; метан — 0,7; воздух — 1,3; углекислый газ — 2,0; пропан — 2,0. 1.3.2 Вязкость Вязкость — это способность жидкости сопротивляться сдвигу, т. е. свойство, обратное текучести (более вязкие жидкости являются менее текучими). Вязкость проявляется в возникновении касательных напряжений (напряжений трения). Рассмотрим слоистое течение жидкости вдоль стенки (рисунок 1.3). В этом случае происходит торможение потока жидкости, обусловленное ее вязкостью. Причем скорость движения жидкости в слое тем ниже, чем ближе он расположен к стенке. Согласно гипотезе Ньютона касательное напряжение, возникающее в слое жидкости на расстоянии у от стенки, определяется зависимостью где dυ/dy — градиент скорости, характеризующий интенсивность нарастания скорости υпри удалении от стенки (по оси у). Зависимость (1.5) называют законом трения Ньютона. Течения большинства жидкостей, используемых в гидравлических системах, подчиняются закону трения Ньютона, и их называют ньютоновскими жидкостями. Однако следует иметь в виду, что существуют жидкости, в которых закон (1.5) в той или иной степени нарушается. Такие жидкости называют неньютоновскими. Величина μ, входящая в (1.5), получила название динамической вязкости жидкости. Она измеряется в Паּс либо в пуазах 1 Пз = 0.1 Па ּс. Однако на практике более широкое применение нашла кинематическая вязкость: Е 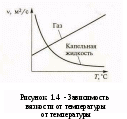 диницей измерения последней в системе СИ является м2/с или более мелкая единица см2/с, которую принято называть стоксом, 1 Ст = 1 см2/с. Для измерения вязкости также используются сантистоксы: 1 сСт = 0,01 Ст. диницей измерения последней в системе СИ является м2/с или более мелкая единица см2/с, которую принято называть стоксом, 1 Ст = 1 см2/с. Для измерения вязкости также используются сантистоксы: 1 сСт = 0,01 Ст.В 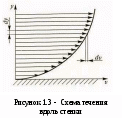 язкость жидкостей существенно зависит от температуры, причем вязкость капельных жидкостей с повышением температуры падает, а вязкость газов — растет (рисунок 1.4). Это объясняется тем, что в капельных жидкостях, где молекулы расположены близко друг к другу, вязкость обусловлена силами молекулярного сцепления. Эти силы с ростом температуры ослабевают, и вязкость падает. В газах молекулы располагаются значительно дальше друг от друга. Вязкость газа зависит от интенсивности хаотичного движения молекул. С ростом температуры эта интенсивность растет и вязкость газа увеличивается. Вязкость жидкостей зависит также от давления, но это изменение незначительно, и в большинстве случаев его не учитывают. 1.3.3 Сжимаемость Сжимаемость — это способность жидкости изменять свой объем под действием давления. Сжимаемость капельных жидкостей и газов существенно различается. Так, капельные жидкости при изменении давления изменяют свой объем крайне незначительно. Газы, наоборот, могут значительно сжиматься под действием давления и неограниченно расширяться при его отсутствии. Для учета сжимаемости газов при различных условиях могут быть использованы уравнения состояния газа или зависимости для политропных процессов [4]. Сжимаемость капельных жидкостей характеризуется коэффициентом объемного сжатия βр (Па-1): где dV— изменение объема под действием давления; dр - изменение давления; V— объем жидкости. Знак минус в формуле обусловлен тем, что при увеличении давления объем жидкости уменьшается, т.е. положительное приращение давления вызывает отрицательное приращение объема. При конечных приращениях давления и известном начальном объеме V0можно определить конечный объем жидкости а также ее плотность Величина, обратная коэффициенту объемного сжатия βр, называется объемным модулем упругости жидкости (или модулем упругости) К = 1/ βр (Па). Эта величина входит в обобщенный закон Гука, связывающий изменение давления с изменением объема Модуль упругости капельных жидкостей изменяется при изменении температуры и давления. Однако в большинстве случаев Kсчитают постоянной величиной, принимая за нее среднее значение в данном диапазоне температур или давлений. Модули упругости некоторых жидкостей (МПа): бензин — 1300; керосин — 1280; вода — 2000; ртуть — 32400; масло гидросистем (АМГ-10) — 1300; масло индустриальное 20 - 1360; масло индустриальное 50 - 1470; масло турбинное — 1700. 1.3.4 Температурное расширение Способность жидкости изменять свой объем при изменении температуры называется температурным расширением. Оно характеризуется коэффициентом температурного расширения βt где dT— изменение температуры; dV— изменение объема под действием температуры; V — объем жидкости. При конечных приращениях температуры Как видно из формул (1.12), (1.13) с увеличением температуры объем жидкости возрастает, а плотность уменьшается. Коэффициент температурного расширения жидкостей зависит от давления и температуры, так для воды при t = 0 0C и p = 0,1 МПа βt = 14·10 –6 1/град, а при t = 100 0C и p = 10 МПа βt = 700·10 –6 1/град, то есть изменяется в 50 раз. Однако на практике обычно принимают среднее значение в данном диапазоне температур и давления. Например, для минеральных масел βt ≈ 800·10 –6 1/град. Газы весьма значительно изменяют свой объем при изменении температуры. Для учета этого изменения используют уравнения состояния газов или формулы политропных процессов [4]. 1.3.5 Испаряемость Любая капельная жидкость способна изменять свое агрегатное состояние, в частности превращаться в пар. Это свойство капельных жидкостей называют испаряемостью. В 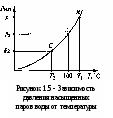 гидравлике наибольшее значение имеет условие, при котором начинается интенсивное парообразование по всему объему — кипение жидкости. Для начала процесса кипения должны быть созданы определенные условия (температура и давление). Например, дистиллированная вода закипает при нормальном атмосферном давлении и температуре 100 °С. Однако это является частным случаем кипения воды. Та же вода может закипеть при другой температуре, если она будет находиться под воздействием другого давления, т. е. для каждого значения температуры жидкости, используемой в гидросистеме, существует свое давление, при котором она закипает. гидравлике наибольшее значение имеет условие, при котором начинается интенсивное парообразование по всему объему — кипение жидкости. Для начала процесса кипения должны быть созданы определенные условия (температура и давление). Например, дистиллированная вода закипает при нормальном атмосферном давлении и температуре 100 °С. Однако это является частным случаем кипения воды. Та же вода может закипеть при другой температуре, если она будет находиться под воздействием другого давления, т. е. для каждого значения температуры жидкости, используемой в гидросистеме, существует свое давление, при котором она закипает. Такое давление называют давлением насыщенных паров рн.п... Величина рнпвсегда приводится как абсолютное давление и зависит от температуры. Для примера на рисунке 1.5 приведена зависимость давления насыщенных паров воды от температуры. На графике выделена точка А, соответствующая температуре 100 °С и нормальному атмосферному давлению ра. Если на свободной поверхности воды создать более высокое давление р1,то она закипит при более высокой температуре Т1(точка В на рисунке 1.5). И наоборот, при малом давлении р2вода закипает при более низкой температуре Т2 (точка С на рисунке 1.5). 1.3.6 Растворимость газов Многие жидкости способны растворять в себе газы. Эта способность характеризуется количеством растворенного газа в единице объема жидкости, различается для разных жидкостей и изменяется с увеличением давления. Относительный объем газа, растворенного в жидкости до ее полного насыщения, можно считать по закону Генри прямо пропорциональным давлению, то есть Vг/Vж= k p/p0, где Vг – объем растворенного газа, приведенный к нормальным условиям (p0 , Т0 ); Vж – объем жидкости; k - коэффициент растворимости; р - давление жидкости. Коэффициент k имеет следующие значения при 20 0С: для воды – 0,016, керосина - 0,13 минеральных масел - 0,08, жидкости АМГ-10 – 0,1. При понижении давления выделяется растворенный в жидкости газ, причем интенсивнее, чем растворяется в ней. Это явление может отрицательно сказывается на работе гидросистем. 2 ГИДРОСТАТИКА 2.1 Свойства гидростатического давления. Основное уравнение гидростатики Гидростатикой называется раздел гидравлики, в котором рассматриваются законы равновесия жидкости и их практическое применение. В покоящейся жидкости возникают только напряжения сжатия и не могут действовать касательные напряжения, так как любое касательное напряжение жидкости вызовет ее движение, т.е. нарушит состояние покоя. В главе 1 было показано, что напряжения сжатия вызывает сила, действующая перпендикулярно на бесконечно малую площадку. Отсюда вытекает первое свойство гидростатического давления: гидростатическое давление действует по нормали к поверхности и является сжимающим, то есть действует внутрь рассматриваемого объема. Второе свойство гидростатического давления состоит в том, что в любой точке внутри покоящейся жидкости гидростатическое давление не зависит от ориентировки площадки, по которой оно действует, то есть одинаково во всех направлениях. Исходя из этих свойств гидростатического давления, можно получить основное уравнение гидростатики. Пусть жидкость находится сосуде, а на ее свободную поверхность действует давление ра .(рисунок2.1). Определим давление р в произвольно выбранной точке, которая находится на глубине h. Д  ля определения искомого давления р вокруг произвольно выбранной точки возьмем бесконечно малую горизонтальную площадку ΔS и построим на ней цилиндр до открытой поверхности жидкости. На выделенный объем жидкости сверху вниз действуют сила, равная произведению давления р0на площадь ΔS, и вес выделенного объема жидкости G. ля определения искомого давления р вокруг произвольно выбранной точки возьмем бесконечно малую горизонтальную площадку ΔS и построим на ней цилиндр до открытой поверхности жидкости. На выделенный объем жидкости сверху вниз действуют сила, равная произведению давления р0на площадь ΔS, и вес выделенного объема жидкости G.В выбранной точке искомое давление р действует по всем направлениям одинаково (второе свойство гидростатического давления). Но на выделенный объем создаваемая этим давлением сила действует по нормали к поверхности и направлена внутрь объема (первое свойство гидростатического давления), т.е. сила направлена вверх и равна произведению р на площадь ΔS. Тогда условием равновесия выделенного объема жидкости в вертикальном направлении будет равенство p∙ ΔS- G -p0 ∙ΔS = 0. Вес G выделенного цилиндра жидкости можно определить, подсчитав его объем V: G= V∙p∙g = ΔS∙h∙ρ ∙g. Подставив математическое выражение для Gв уравнение равновесия и решив его относительно искомого давления р, окончательно получим p = p0 + ρ g h. (2.1) Полученное уравнение называют основным уравнением гидростатики. Оно позволяет подсчитать давление в любой точке внутри покоящейся жидкости, как сумму давления p0на внешней поверхности жидкостии давления , обусловленного весом вышележащих слоев жидкости - ρ gh. Величина р0является одинаковой для всех точек объема жидкости, поэтому учитывая свойства гидростатического давления, можно сказать, что давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости и по всем направлениям одинаково. Это положение известно под названием закона Паскаля. Давление жидкости, как видно из формулы (2.1), возрастает с увеличением глубины по линейному закону и на данной глубине есть величина постоянная. Поверхность, давление во всех точках которой одинаково, называется поверхностью уровня. В случае, когда на жидкость действует только сила тяжести, поверхности уровня представляют собой горизонтальные плоскости, при этом свободная поверхность является одной из поверхностей уровня. Возьмем на произвольной высоте горизонтальную плоскость сравнения. Обозначив через z расстояние от этой плоскости до рассматриваемой точки, через z0 - расстояние до свободной поверхности и заменив в уравнении (2.1) h на z – z0, получим основное уравнение гидростатики в другой форме: Так как рассматриваемая точка выбрана произвольно, можно утверждать, что для любой точки неподвижного объема жидкости Координата zназывается геометрической высотой, величина р / ρg – пьезометрической высотой, а их сумма - гидростатическим напором. Таким образом, гидростатический напор есть величина постоянная для всего объема неподвижной жидкости. Основное уравнение гидростатики широко применяется для решения практических задач. Однако при его использовании в практических расчетах следует обращать особое внимание на высоту h, так как она может принимать как положительные, так и отрицательные значения. Действительно, если точка, в которой определяем давление, располагается ниже точки с исходным давлением, то в математической записи основного закона гидростатики ставится знак «+», как в формуле (2.1). А в том случае, когда точка, в которой определяем давление, располагается выше точки с исходным давлением, в уравнении знак « + » изменяется на « - », то есть ро = р – ρgh. При выборе знака в основном законе гидростатики всегда следует помнить, что чем ниже (глубже) располагается точка в данной жидкости, тем больше давление в этой точке. В заключение следует добавить, что основное уравнение гидростатики широко используется при измерении давлений. 2.2 Устройство и приборы для измерения давления К 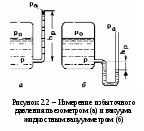 ак было показано в главе 1, давление может быть абсолютным, избыточным и давлением вакуума. В машиностроительной гидравлике наиболее часто используются давления избыточные и вакуума, поэтому измерению этих давлений уделим наибольшее внимание. ак было показано в главе 1, давление может быть абсолютным, избыточным и давлением вакуума. В машиностроительной гидравлике наиболее часто используются давления избыточные и вакуума, поэтому измерению этих давлений уделим наибольшее внимание.Простейшим прибором для измерения избыточного давления является пьезометр, который представляет собой вертикально установленную прозрачную трубку, верхний конец которой открыт в атмосферу, а нижний присоединен к емкости, в которой измеряется давление (рисунок 2.2, а). Применяя формулу (2.1) к жидкости, заключенной в пьезометре, получим рабс = рa + ρghp, где рабс - абсолютное давление в жидкости на уровне присоединения пьезометра, рa - атмосферное давление. Отсюда высота подъема жидкости в пьезометре (пьезометрическая высота) Таким образом, пьезометрическая высота представляет собой высоту столба жидкости, соответствующую избыточному давлению в данной точке. Измерения по пьезометру проводят в единицах длины, поэтому иногда давления выражают в единицах высоты столба определенной жидкости. Например, атмосферное давление, равное 760 мм рт. ст., соответствует высоте ртутного столба 760 мм в пьезометре. Подставив это значение в уравнение (2.3) при ρрт = 13600 кг/м3, получим атмосферное давление, равное 1,013 • 105 Па. Эта величина называетсяфизической атмосферой. Она отличается от технической атмосферы, которая соответствует 736 мм рт. ст. Это число можно получить, если подставить в формулу (2.3) ризб= 1 ат и вычислить высоту hp. С помощью стеклянной трубки можно измерить и давление вакуума, при этом жидкость в трубке опустится ниже уровня измерения (см. рисунок 2.2,б). В этом случае рабс = рa - ρghp, откуда Формула (2.4) позволяет определить максимальную высоту всасывания жидкости. Полагая рабс = 0 и не учитывая давления насыщенных паров, получаем При нормальном атмосферном давлении (0,1033 МПа) высота Нmax для воды равна 10.33 м, для бензина – 13,8 м, для ртути – 0,760 м и так далее. С  хемы наиболее распространенных жидкостных манометров и вакуумметров представлены на рисунке 2.3. Рисунок 2.3 – Схемы жидкостных манометров: а) U – образный манометр; б) чашечный манометр; в) дифференциальный манометр; г) двух-жидкостный микроманометр; д) двух-жидкостный чашечный манометр. П  ьезометры просты по конструкции и обеспечивают высокую точность измерений. Однако они не позволяют измерять большие давления. Подтвердим это на следующем примере. Пусть пьезометром необходимо измерить избыточное давление риз6= 0,1 МПа ≈ 1 ат в жидкости с плотностью, равной плотности воды (ρ= 1000 кг/м3). Тогда из формулы (2.3) при заданных условиях получим высоту столба воды в пьезометре Н ≈ 10 м, что является весьма значительнойвеличиной. В машиностроении используются более высокие давления (в сотни атмосфер), что ограничивает применение пьезометров. ьезометры просты по конструкции и обеспечивают высокую точность измерений. Однако они не позволяют измерять большие давления. Подтвердим это на следующем примере. Пусть пьезометром необходимо измерить избыточное давление риз6= 0,1 МПа ≈ 1 ат в жидкости с плотностью, равной плотности воды (ρ= 1000 кг/м3). Тогда из формулы (2.3) при заданных условиях получим высоту столба воды в пьезометре Н ≈ 10 м, что является весьма значительнойвеличиной. В машиностроении используются более высокие давления (в сотни атмосфер), что ограничивает применение пьезометров. Аналогичные по принципу работы приборы с использованием ртути позволяют в 13,6 раза уменьшить пьезометрические высоты (ртуть в 13,6 раза тяжелее воды). Но ртуть ядовита, и такие приборы в машиностроении практически перестали применяться. Широкое распространение в технике для измерения давлений получили пружинные манометры. Основным элементом такого прибора (рисунок 2.4) является пружинящая тонкостенная трубка 1 (обычно латунная). Один из концов трубки запаян и подвижен, а второй закреплен, и к нему подводится измеряемое давление. Подвижный конец трубки 1 кинематически связан со стрелкой 3. При изменении давления он изменяет свое положение и перемещает стрелку 3, которая указывает на соответствующее число на шкале 2. Пружинные приборы для измерения вакуума не имеют ни принципиальных, ни конструктивных отличий от пружинных манометров. Устройства для измерения вакуума получили название вакуумметров. Выпускаются также приборы, позволяющие измерять как избыточные давления, так и вакуум. Их принято называть мановакуумметрами. В метеорологии измерение абсолютных значений атмосферных давлений проводят с помощью барометров. Для машиностроительных систем измерение абсолютных давлений практического значения не имеет. 2.3 Сила давления на плоскую стенку Д  о сих пор рассматривались давления, действующие в жидкости. Однако более важное практическое значение имеют силы, возникающие от действия жидкости на различные стенки. о сих пор рассматривались давления, действующие в жидкости. Однако более важное практическое значение имеют силы, возникающие от действия жидкости на различные стенки.При определении силы, действующей со стороны жидкости на плоскую стенку, рассмотрим общий случай, когда стенка наклонена к горизонту под углом α, а на свободную поверхность жидкости действует давление р0(рисунок 2.5). Вычислим силу давления F, действующую на некоторый участок рассматриваемой стенки площадью S. Ось Ох направим по линии пересечения плоскости стенки со свободной поверхностью жидкости, а ось Оу — перпендикулярно к этой линии в плоскости стенки. Выразим сначала элементарную силу давления, приложенную к бесконечно малой площадке dS: dF = p dS = (pо + ρ gh) dS = pоdS + ρ g h d S, где ро — давление на свободной поверхности; h — глубина расположения площадки dS. Для определения полной силы Fпроинтегрируем полученное выражение по всей площади S: где у — координата площадки dS. Последний интеграл представляет собой статический момент площади Sотносительно оси Ох и равсн произведению этой площади на координату ее центра тяжести (точка С), то есть Следовательно здесь hс — глубина расположения центра тяжести площади S. |
