Гидравлика. Введение гидравлика относится к числу древнейших наук

• Название: Введение гидравлика относится к числу древнейших наук
• Анкор: Гидравлика
• Дата: 27.10.2022
• Размер: 5.48 Mb.
• Имя файла: c6dfbb4.doc
• Тип: Документы; #757246
• страница: 4 из 8

Отсюда

,

ч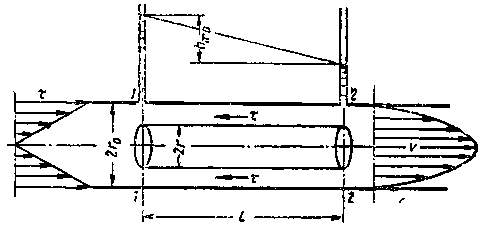

Рисунок 3.12 - Схема ламинарного течения жидкости в трубе

то и показывают пьезометры, установленные в этих сечениях.
В потоке жидкости выделим цилиндрический объем радиусом r, соосный с трубой и имеющий основания в выбранных сечениях. Запишем уравнение равномерного движения выделенного объема жидкости в трубе, т.е. равенство нулю суммы сил, действующих на объем: сил давления и сопротивления. Обозначая касательное напряжение на боковой поверхности цилиндра через τ, получим



откуда



Из формулы следует, что касательные напряжения в поперечном сечении трубы изменяются по линейному закону в функции радиуса. Эпюра касательного напряжения показана на рисунке 3.12, слева.

Выразим касательное напряженно τ по закону трения Ньютона через динамическую вязкость и поперечный градиент скорости; при этом заменим переменное у (расстояние от стенки) текущим радиусом r:



Знак минус обусловлен тем, что направление отсчета r(от оси к стенке) противоположно направлению отсчета у (от стенки).

Подставляя значение τ в предыдущее уравнение, получаем

.

Найдем отсюда приращение скорости



При положительном приращении радиуса получается отрицательное приращение (уменьшение) скорости, что соответствует профилю скоростей, показанному на рисунке 3.12.

Выполнив интегрирование, получим



Постоянную интегрирования С найдем из условия, что на стенке при r = r₀ υ = 0:

,

тогда скорость по окружности радиусом r

. (3.20)

Это выражение является законом распределения скоростей по сечению круглой трубы при ламинарном течении. Кривая, изображающая эпюру скоростей, является параболой второй степени.

Максимальная скорость, имеющая место в центре сечения (при r = 0),

. (3.21)

Входящее в формулу (3.20) отношение p_тр/l(см. рисунок 3.12) представляет собой гидравлический (пьезометрический) уклон, умноженный на ρg. Эта величина является постоянной вдоль прямой трубы постоянного диаметра.

Применим полученный закон распределения скоростей, описываемый уравнением (3.20) для расчета расхода. Для этого выразим сначала элементарный расход через бесконечно малую площадку dS:



Здесь есть функция радиуса, определяемая формулой (3.20), а площадку dSцелесообразно взять в виде кольца радиусом r и шириной dr, тогда



После интегрирования по всей площади поперечного сечения, т.е. от r = 0 до r = r₀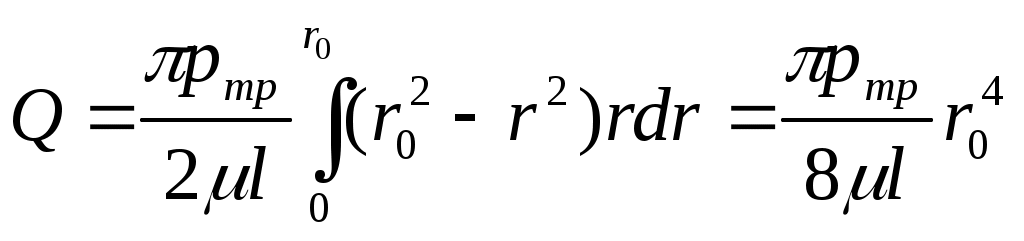

(3.22)

Среднюю по сечению скорость найдем делением расхода на площадь. С учетом выражения (3.22) получим

(3.23)

Сравнение этого выражения с формулой (3.20) показывает, что средняя скорость при ламинарном течении в 2 раза меньше максимальной:

Для получения закона сопротивления, т.е. выражения потери напора h_тр на трение через расход и размеры трубы, определим p_тр из формулы (3.22)



Разделив это выражение на ρg, заменив µ на νρ и p_тр на h_трρg, а также перейдя от r₀ к

d = 2r₀, найдем

(3.24)

Полученный закон сопротивления показывает, что при ламинарном течении в трубе круглого сечения потеря напора на трение пропорциональна расходу и вязкости в первой степени и обратно пропорциональна диаметру в четвертой степени. Этот закон, обычно называемый законом Пуазейля, используется для расчета трубопроводов с ламинарным течением.

Заменим в формуле (3.24) расход произведением . После сокращений получим

(3.25)

Данное выражение известно как закон Стокса. Приведем закон сопротивления Стокса к виду формулы Вейсбаха-Дарси:

.

Для этого умножим и разделим формулу (3.25) на , перегруппировав сомножители, после сокращений получим

,

откуда следует, что при ламинарном режиме

. (3.26)

где λ_л— коэффициент потерь на трение для ламинарного течения:

Изложенная теория ламинарного течения жидкости в круглой трубе хорошо подтверждается опытом, и выведенный закон сопротивления обычно не нуждается в каких-либо поправках, за исключением следующих случаев:

1) при течении в начальном участке трубы, где происходит постепенное формирование параболического профиля скоростей;

2) при течении с теплообменом;

3) при течении в капиллярах и зазорах с облитерацией;

4) при течении с большими перепадами давления.

Участок от начала трубы, на котором формируется (стабилизируется) параболический профиль скоростей, называется начальным участком течения (l_нач). За пределами этого участка имеем стабилизированное ламинарное течение, параболический профиль скоростей остается неизменным, как бы ни была длинна труба, при условии сохранения ее прямолинейности и постоянства сечения. Изложенная выше теория ламинарного течения справедлива именно для этого стабилизированного ламинарного течения и неприменима в пределах начального участка.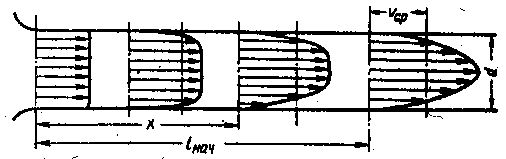



Рисунок 3.13 - Формирование профиля скоростей на начальном участке



Для определения длины начального участка можно пользоваться приближенной формулой Шиллера, выражающей эту длину, отнесенную к диаметру трубы, как функцию числа Re:

. (3.27)

Сопротивление на начальном участке трубы получается больше, чем на последующих участках. Объясняется это тем, что значений производной dυ/dyу стенки трубы на начальном участке больше, чем на участках стабилизированного течения, а потому больше и касательное напряжение, определяемое законом Ньютона, и притом тем больше, чем ближе рассматриваемое сечение к началу трубы, т.е. чем меньше координата x.

Потеря напора на участке трубы, длина которого l l_нач, определяется по формуле

(3.28)

Закономерности ламинарного течения с теплообменом и большими перепадами давления подробно рассмотрены в [1].

3.9 Турбулентное течение
3.9.1 Основные сведения
Турбулентное течение характеризуется перемешиванием жидкости, пульсациями скоростей и давлений. Если с помощью особо чувствительного прибора-самописца измерить и записать пульсации, например, скорости по времени в фиксированной точке потока, то получим картину, подобную показанной на рисунке 3.14. Скорость беспорядочно колеблется около некоторого осредненного υ_оср по времени значения, которое в данном случае остается постоянным.

Траектории частиц, проходящих через данную неподвижную точку пространства в разные моменты времени, представляют собой кривые линии различной формы, несмотря на прямолинейность трубы. Характер линий тока в трубе в данный момент времени также отличается большим разнообразием (рисунок 3.15).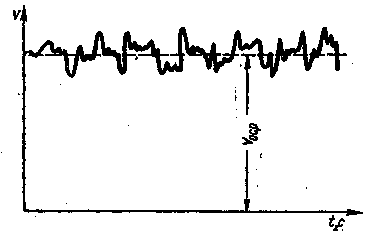




Рисунок 3.14 - Пульсация скорости в турбулентном потоке





Рисунок 3.15 - Характер линий тока в турбулентном потоке



Таким образом турбулентное течение всегда является неустановившимся, так как значения скоростей и давлений, а также траектории частиц, изменяются по времени. Однако его можно рассматривать как установившееся течение при условии, что осредненные по времени значения скоростей и давлений, а также полный расход потока не изменяются со временем. Такое течение на практике считают приближенно стационарным или квазистационарным.

Распределение скоростей (осредненных по времени) в поперечном сечении турбулентного потока существенно отличается от того, которое характерно для ламинарного течения. Если сравним кривые распределения скоростей в ламинарном и турбулентном потоках в одной и той же трубе и при одном и том же расходе (одинаковой средней скорости), то обнаружим существенное различие (рисунок 3.16). Распределение скоростей при турбулентном течения более равномерное, а нарастание скорости у стенки более крутое, чем при ламинарном течении, для которого характерен параболический закон распределения скоростей.

В связи с этим коэффициент Кориолиса α, учитывающий неравномерность распределения скоростей в уравнении Бернулли при турбулентном течении значительно меньше, нежели при ламинарном. В отличие от ламинарного течения, где α не зависит от Re и равен 2, здесь коэффициент α является функцией Re и уменьшается с увеличением последнего от 1,13 приRe = Re_кр до 1,025 при Re = 3·10⁶. Как видно из графика, приведенного на рис. 3.17, кривая α при возрастании числа Re приближается к единице, поэтому в большинстве случаев при турбулентном течении можно принимать α = 1.

Так как при турбулентном течении отсутствует слоистость потока и происходит перемешивание жидкости, закон трения Ньютона в этом случае выражает лишь малую часть полного касательного напряжения. Благодаря перемешиванию жидкости и непрерывному переносу количества движения в поперечном направлении касательное напряжение τ₀ на стенке трубы в турбулентном потоке значительно больше, чем в ламинарном, при тех же значениях числа Re и динамического давления ρυ²/2, подсчитанных по средней скорости потока.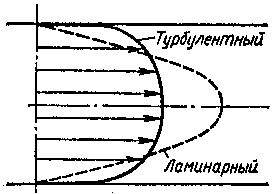




Рисунок 3.16 - Профили скоростей в ламинарном и турбулентном потоках



Рисунок 3.17 - Зависимость коэффициента α от lg Re



В связи с этим потери энергии при турбулентном течении жидкости в трубах также получаются иными, нежели при ламинарном. В турбулентном потоке при Re > Re_кp потери напора на трение по длине значительно больше, чем при ламинарном течении при тех же размерах трубы, расходе и вязкости жидкости, а следовательно, при одинаковых числах Re (ламинарный режим при этом неустойчив).

Если при ламинарном течении потеря напора на трение возрастает пропорционально скорости (расходу) в первой степени, то при переходе к турбулентному течению заметны некоторый скачок сопротивления и затем более крутое нарастание величины h_тр по кривой, близко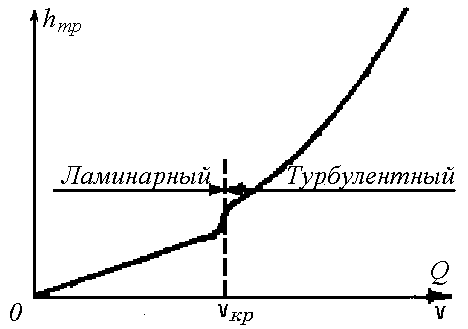
Рисунок 3.18 - Зависимость h_тр от υ и Q
й к параболе второй степени (рисунок 3.18).

Ввиду сложности турбулентного течения и трудностей его аналитического исследования до настоящего времени для него нет достаточно строгой и точной теории. В большинстве случаев для практических расчетов, связанных с турбулентным течением жидкостей в трубах, пользуются экспериментальными данными, систематизированными на основе теории гидродинамического подобия. Важное значение при этом имеет движение жидкости непосредственно на стенке трубы. Здесь имеется тонкий подслой, в котором превалируют силы вязкости, а движение происходит без перемешивания (см. рисунок 3.19). Этот слой называется ламинарным (вязким). В его пределах скорость круто нарастает от нуля на стенке до некоторой конечной величины υ_л на границе слоя. Толщина δ_л ламинарного слоя крайне невелика, причем оказывается, что число Re, подсчитанное но толщине δ_л, скорости υ_л и кинематической вязкости ν, есть величина постоянная, т. е.

.

Эта величина в соответствии с теорией гидродинамического подобия имеет универсальное постоянное значение подобно тому, как постоянно Re_кp для течения в трубах. Поэтому при увеличении скорости потока и, следовательно, Re растет также скорость υ_ла толщина δ_л ламинарного слоя уменьшается.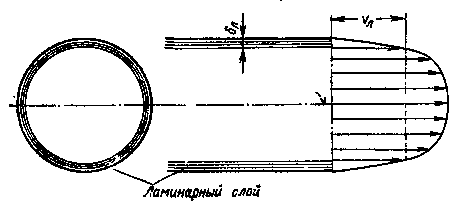




Рисунок 3.19 -. Ламинарный пристенный слой при турбулентном течении в трубе
Основной расчетной формулой для потерь напора при турбулентном течении в круглых трубах является уже приводившаяся выше эмпирическая формула, называемая формулой Вейсбаха— Дарси и имеющая следующий вид:

, (3.29)

где λ_т— коэффициент потерь на трение при турбулентном течении, или коэффициент Дарси.

Эта основная формула применима как при турбулентном, так и при ламинарном течении, различие заключается лишь в значениях коэффициента λ.
3.9.2 Определение коэффициента потерь на трение. Исследования И. Никурадзе
Для определения λ при турбулентном режиме предложен ряд эмпирических и полуэмпирических формул, полученных многими авторами в результате исследования различных областей гидравлического трения. Однако фундаментальным исследованием стала работа И. И. Никурадзе, который в 1933 г. опубликовал результаты своих многочисленных опытов, представленных в виде особого графика.

В


Рисунок 3.20 – График Никурадзе
своих опытах Никурадзе исследовал напорное движение жидкости в круглоцилиндрических трубах, имеющих однозернистую равномерно распределенную (равнозернистую) шероховатость, которую он создавал путем наклеивания калиброванных песчинок высотой Δ на внутреннюю поверхность трубы.

Полученный Никурадзе график представляет собой семейство кривых, построенных в логарифмических координатах (по горизонтальной оси отложены величины lg Re_D, а по вертикальной — lg 100λ) по точкам, соответствующим опытам с трубами с различной относительной шероховатостью Δ_r = Δ : D, от Δ_r = 0,00197 до Δ_r = 0,0666.

Рассмотрим подробно график Никурадзе (рисунок 3.20). Все поле графика можно условно разбить на пять областей.

Первая область — область ламинарного режима при Re < 2300, (lg Re≤3,36), здесь все опытные точки независимо от шероховатости уложились на одну прямую линию I, уравнение которой λ = 64 / Re.

Вторая область, расположенная между вертикалями III и IV, — область неустойчивого режима или переходная (числа Рейнольдса лежат в пределах от 2300 до 10000). Здесь возможно существование как ламинарного, так и турбулентного режимов, экспериментальные точки имеют значительный разброс.

Третья область — область гидравлически гладких труб» при турбулентном режиме, здесь толщина вязкого подслоя существенно больше высоты выступов шероховатости и турбулентное ядро потока не соприкасается с ними. Поэтому в этой области коэффициент λ = f(Re) не зависит от шероховатости. Область гладких труб представлена на графике прямой линией II, уравнение которой

. (3.30)

Эта эмпирическая формула была получена Блазиусом в 1913г. в результате обработки многочисленных опытов по исследованию движения жидкости в круглых гладких латунных трубах при числах Рейнольдса Re от 2300 до 100000.

Четвертая область — область турбулентного режима доквадратичного сопротивления шероховатых труб, лежит между прямой II и линией АВ, образованной точками, отделяющими горизонтальные участки кривых с некоторой заданной точностью. Можно видеть, что в этой области каждая кривая отвечает определенному значению относительной шероховатости. Здесь турбулентное ядро постепенно раскрывает шероховатость, поэтому имеет место наиболее общий случай λ = f(Re,Δ_r).

Пятая область — область турбулентного режима квадратичного сопротивления шероховатых труб, располагается правее и выше линий АВ. Здесь коэффициент λне зависит от числа Рейнольдса Re (все линии графика — прямые, параллельные горизонтальной оси). Коэффициент λ, а следовательно, и потеря напора h_тр зависят от шероховатости λ = f (Δ_r). Таким образом, как видно из формулы Вейсбаха - Дарси, для этой области сопротивления потеря напора по длине прямо пропорциональна квадрату средней скорости.

В заключение необходимо отметить, что общий качественный характер зависимостей коэффициента гидравлического трения λ, полученный Никурадзе для труб круглого сечения, распространяется и на другие потоки, в том числе ибезнапорные, что было подтверждено опытами А. П. Зегжды, в которых исследовалось безнапорное движение жидкости в лотке прямоугольного сечения, имеющего различную равнозернистую шероховатость. Важно также подчеркнуть, что после указанных работ отпала необходимость создавать особые расчетные зависимости для различных жидкостей, так как род жидкости учитывается числом Рейнольдса.