Гидравлика. Введение гидравлика относится к числу древнейших наук
 Скачать 5.48 Mb.
|
Уравнение Бернулли широко применяется в технике, как для выполнения гидравлических расчетов, так и для решения ряда практических задач. Одной из таких задач является измерение скорости и расхода жидкости. Рассмотрим некоторые устройства для измерения расхода и скорости жидкости. Р 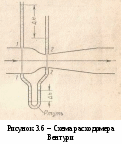 асходомер Вентури представляет собой устройство, устанавливаемое в трубопроводах и осуществляющее сужение потока - дросселирование (рисунок 3.6). Расходомер состоит из двух участков - плавно сужающегося (сопла) и постепенно расширяющегося (диффузора). Скорость потока в суженном месте возрастает, а давление падает. Возникает разность (перепад) давлений, которая измеряется двумя пьезометрами или дифференциальным U-образным манометром и определенным образом связана с расходом. Найдем эту связь. Допустим в сечении 1-1 потока непосредственно перед сужением скорость потопа равна υ1, давление р1, площадь сечении S1, а в сечении 2-2, т. е. в самом узком месте потока, соответственно υ2, р2, S2. Разность показаний пьезометров, присоединенных к указанным сечениям ΔН.Запишем для сечений 1—1 и 2—2 потока уравнение Бернулли и уравнение расхода (считая распределение скоростей равномерным):  где hм — потеря напора между сечениями 1-1 и 2-2. Учитывая, что  и  найдем из этой системы уравнений одну из скоростей, например 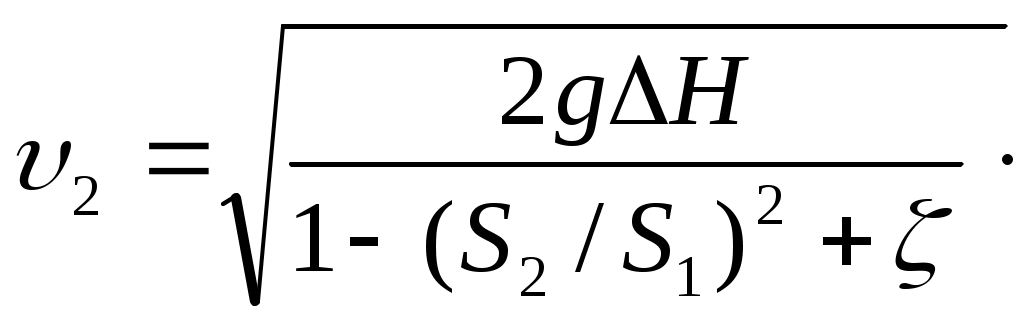 ,отсюда объемный расход  (3.17)или  , (3.18)где С – величина, постоянная для данного расходомера. Зная величину С и наблюдая за показанием пьезометра, можно найти расход в трубопроводе для любого момента временя по формуле (3.18). Константу С можно определить теоретически, но точнее ее можно найти экспериментально, т. е. в результате градуирования расходомера. Связь между ΔН и Q получается параболической, а если по оси абсцисс откладывать расход во второй степени, то график этой зависимости будет представлять собой прямую. Очень часто вместо пары пьезометров для измерения перепада давления в расходомере применяют дифференциальный ртутный манометр. Учитывая, что над ртутью в трубках находится та же жидкость плотностью ρ, можно записать  Т  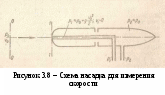 рубка полного напора (или трубка Пито) служит для измерения скорости, например, в трубе (рисунок 3.7). Если установить в этом потоке трубку, изогнутую под углом 90°, отверстием навстречу потоку и пьезометр, то жидкость в этой трубке поднимается над уровнем в пьезометре на высоту, равную скоростному напору. Объясняется это тем, что скорость υ частиц жидкости, попадающих в отверстие трубки, уменьшается до нуля, а давление, следовательно, увеличивается на величину скоростного напора. Измерив разность высот подъема жидкости в трубке Пито и пьезометре, легко определить скорость жидкости в данной точке. На этом же принципе основано измерение скорости полета самолета. На рисунке 3.7 показана схема самолетной скоростной трубки (насадка) для измерения малых по сравнению со скоростью запуска скоростей полета. Запишем уравнение Бернулли для струйки, которая набегает на трубку вдоль ее оси, а затем растекается по ее поверхности. Для сечений 0-0 (невозмущенный поток) и 1-1 (где υ = 0), получаем  Так как боковые отверстия трубки приближенно воспринимают давление невозмущенного потока, р2 ≈ р0, следовательно из предыдущего имеем  .Другим важным случаем практического использования уравнения Бернулли является создание топливно-воздушной смеси для двигателей внутреннего сгорания с помощью карбюратора и эжектора. Карбюратор поршневых двигателей внутреннего сгорания служит для подсоса бензина и смешения его с потоком воздуха (рисунок 3.9). Поток воздуха; засасываемого в двигатель, сужается в том месте, где установлен распылитель бензина (обрез трубки диаметром d). Скорость воздуха в этом сечении возрастает, а давление по закону Бернулли падает. Благодаря пониженному давлению бензин вытекает в поток воздуха. Найдем соотношение между массовыми расходами бензина Qб и воздуха Qв при заданных размерах D и d и коэффициентах сопротивления воздушного канала (до сечения 2-2) ζв и жиклера ζж (сопротивлением бензотрубки пренебрегаем). З 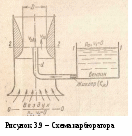 аписав уравнение Бернулли для потока воздуха (сечение 0-0 и 2-2), а затем для потока бензина (сечение 1-1 и 2-2), получим (при z1 = z2 и α = 1):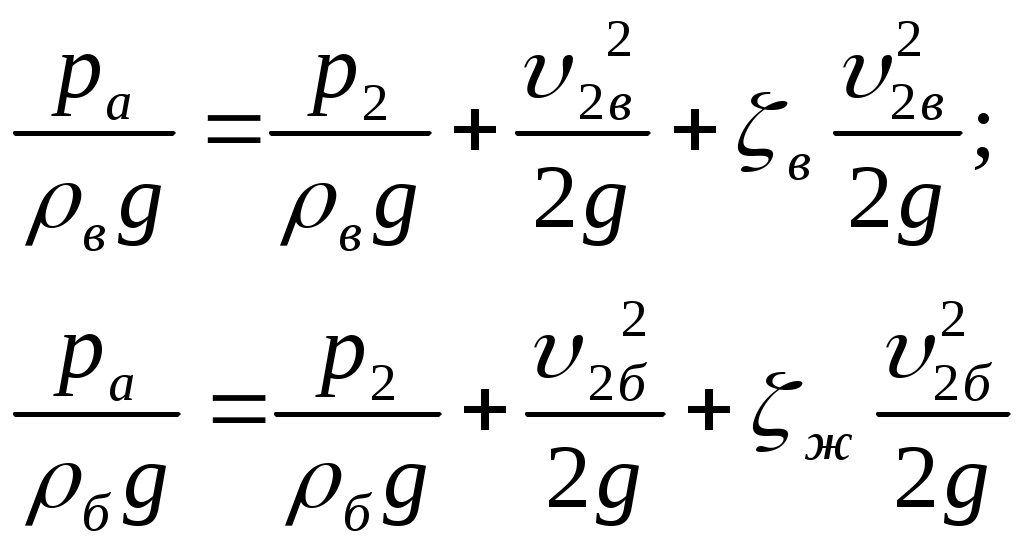 откуда  Учитывая, что массовые расходы 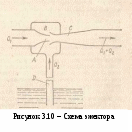 и  , получим Т  аким образом обеспечивается постоянство соотношения расходов бензина и воздуха. Однако следует иметь в виду приближенный характер данного решенияСтруйный насос (эжектор) состоит из плавно сходящегося насадка А (рисунок 3.10), осуществляющего сжатие потока, и постепенно расширяющейся трубки С, установленной на некотором расстоянии от насадка в камере В. Вследствие увеличения скорости потока давление в струе на выходе из насадка и по всей камере В и значительно понижается. В расширяющейся трубке скорость уменьшается, а давление возрастает приблизительно до атмосферного (если жидкость вытекает в атмосферу), следовательно, в камере В давление обычно меньше атмосферного, т.е. возникает разрешение (вакуум). Под действием разрежения жидкость из нижнего резервуары всасывается по трубе D в камеру В, где происходят слияние и дальнейшее перемешивание двух потоков. 3.7 Режимы течения жидкости в трубах Опыты показывают, что возможны два режима или два вида течения жидкостей и газов в трубах: ламинарный и турбулентный. Указанные течения жидкости можно наблюдать на приборе, представленном на рисунке 3.11. Он состоит из резервуара А с водой, от которого отходит стеклянная труба В с краном С па конце, и сосуда D с индикаторной подкрашенной жидкостью, которая может по трубке вводиться тонкой струйкой внутрь стеклянной трубы В. Е 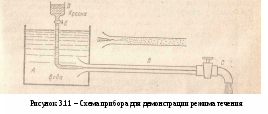 сли несколько приоткрыть кран С и дать возможность воде протекать в трубе с небольшой скоростью, а затем с помощью крана Е впустить индикаторную жидкость в поток воды, то увидим, что введенная в трубу подкрашенная жидкость не будет перемешиваться с потоком воды. Струйка краски будет отчетливо видимой вдоль всей стеклянной трубы, что указывает на слоистый характер течения жидкости и на отсутствие перемешивания. Пьезометр или трубка Пито, присоединенные к трубе, покажут неизменность давления и скорости по времени, отсутствие колебаний (пульсаций). Это так называемое ламинарное (слоистое) течение. При постепенном увеличении скорости течения воды в трубе путем открытии крана С картина течения вначале не меняется, но затем при определенной скорости течения наступает быстрое ее изменение. Струйка подкрашенной жидкости по выходе из трубки начинает колебаться, затем размываться и перемешиваться с потоком воды, причем становятся заметными вихреобразования и вращательное движение жидкости. Пьезометр и трубка Пито показывают непрерывные пульсации давления и скоростей в потоке воды. Течение становится, как его принято называть, турбулентным (см. рисунок3.11, вверху). Если уменьшить скорость потока, то восстановится ламинарное течение. Итак, ламинарным называется слоистое течение без перемешивания частиц жидкости и без пульсаций скоростей и давления. При таком течении все линии тока определяются формой русла, по которому течет жидкость. При ламинарном течении жидкости в прямой трубе постоянного сечения все линии тока направлены параллельно оси трубы, т. е. прямолинейно; отсутствуют поперечные перемещения жидкости. Турбулентным называется течение, сопровождающееся интенсивным перемешиванием жидкости и пульсациями скоростей и давлений. При турбулентном течении векторы скоростей имеют не только осевые, но и нормальные составляющие, поэтому наряду с основным продольным перемещением жидкости вдоль русла происходят поперечные перемещения (перемешивание) и вращательное движение отдельных объемов жидкости. Режим течения данной жидкости в данной трубе изменяется при вполне определенной средней по сечению скорости течения υ кр, которую называют критической. Как показывают опыты, значение этой скорости прямо пропорционально кинематической вязкости v и обратно пропорционально диаметру d трубы, т. с.  .Входящий в эту формулу безразмерный коэффициент пропорциональности kодинаков для всех жидкостей и газов, а также для любых диаметров труб. Это означает, что изменение режима течения происходит при определенном соотношении между скоростью, диаметром и вязкостью v: k = υкр d/v. Полученное безразмерное число называется критическим числом Рейнольдса и обозначается Reкр = υкрd/v. (3.19) Критическое число Рейнольдса Reкр не зависит от рода жидкости и размеров сечения, а лишь в небольшой степени определяется формой сечения и шероховатостью стенок трубы. Таким образом, критическое число Рейнольдса является критерием, определяющим режим течения в трубах. Как показывают опыты, для труб круглого сечения Reкр ≈ 2300. Зная скорость движения жидкости, ее вязкость и диаметр трубы, можно расчетным путем найти число Re и, сравнив его с Reкр, определить режим течения жидкости. При Re < Reкр течение является ламинарным, при Re > Reкр — турбулентным. Точнее говоря, вполне развитое турбулентное течение в трубах устанавливается лишь при Re ≥ 10000, а при Re = 2300 … 10000 имеет место переходная, критическая область. На практике имеют место как ламинарное, так и турбулентное течения, причем первое наблюдается в основном в тех случаях, когда по трубам движутся весьма вязкие жидкости, например смазочные масла, второе обычно происходит в водопроводах, а также в трубах, по которым перетекают бензин, керосин, спирты, кислоты и другие маловязкие жидкости. 3.8 Теория ламинарного течения в круглых трубах Как указывалось ранее, ламинарное течение является строго упорядоченным, слоистым течением без перемешивания жидкости. Теория ламинарного течения жидкости основывается на законе трения Ньютона. Это трение между слоями движущейся жидкости является единственным источником потерь энергии в данном случае. Рассмотрим установившееся ламинарное течение жидкости в прямой круглой цилиндрической трубе с внутренним диаметром d= 2r0. Чтобы исключить влияние силы тяжести и этим упростить вывод, допустим, что труба расположена горизонтально. Достаточно далеко от входа в нее, где поток уже вполне сформировался (стабилизировался), выделим отрезок длиной lмежду сечениями 1-1и 2-2. Пусть в сечении 1-1 давление равно р1, а в сечении 2-2 р2.Ввиду постоянства диаметра трубы, скорость жидкости будет постоянной, а коэффициент а будет неизменным вдоль потока вследствие его стабильности, поэтому уравнение Бернулли для выбранных сечении примет вид  ,где hтр — потеря напора на трение по длине. |
