высшая матем. Введение теория вероятностей является одним из классических разделов математики

• Название: Введение теория вероятностей является одним из классических разделов математики
• Дата: 27.09.2021
• Размер: 88.38 Kb.
• Имя файла: высшая матем.docx
• Тип: Документы; #237800

ВВЕДЕНИЕ

Теория вероятностей является одним из классических разделов математики. Она имеет длительную историю. Основы этого раздела науки были заложены великими математиками. Назову, например, Ферма, Бернулли, Паскаля. Позднее развитие теории вероятностей определились в работах многих ученых. Большой вклад в теорию вероятностей внесли ученые нашей страны: П.Л.Чебышев, А.М.Ляпунов, А.А.Марков, А.Н.Колмогоров. Вероятностные и статистические методы в настоящее время глубоко проникли в приложения. Они используются в физике, технике, экономке, биологии и медицине. Особенно возросла их роль в связи с развитием вычислительной техники.

Например, для изучения физических явлений производят наблюдения или опыты. Их результаты обычно регистрируют в виде значений некоторых наблюдаемых величин. При повторении опытов мы обнаруживаем разброс их результатов. Например, повторяя измерения одной и той же величины одним и тем же прибором при сохранении определенных условий (температура, влажность и т.п.), мы получаем результаты, которые хоть немного, но все же отличаются друг от друга. Даже многократные измерения не дают возможности точно предсказать результат следующего измерения. В этом смысле говорят, что результат измерения есть величина случайная. Еще более наглядным примером случайной величины может служить номер выигрышного билета в лотерее. Можно привести много других примеров случайных величин. Все же и в мире случайностей обнаруживаются определенные закономерности. Математический аппарат для изучения таких закономерностей и дает теория вероятностей. Таким образом, теория вероятностей занимается математическим анализом случайных событий и связанных с ними случайных величин.

ГЛАВА 1. ПОНЯТИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

В том случае, если случайное событие выражается в виде числа, можно говорить о случайной величине. Случайной называют величину, которая в результате испытания примет одно возможное значение, наперёд неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.

Выпадение некоторого значения случайной величины Х это случайное событие: Х = х_i. Среди случайных величин выделяют дискретные и непрерывные случайные величины.

Дискретной случайной величиной называется случайная величина, которая в результате испытания принимает отдельные значения с определёнными вероятностями. Число возможных значений дискретной случайной величины может быть конечным и бесконечным. Примеры дискретной случайной величины: запись показаний спидометра или измеренной температуры в конкретные моменты времени.

Непрерывной случайной величиной называют случайную величину, которая в результате испытания принимает все значения из некоторого числового промежутка. Число возможных значений непрерывной случайной величины бесконечно. Пример непрерывной случайной величины: измерение скорости перемещения любого вида транспорта или температуры в течение конкретного интервала времени.

Любая случайная величина имеет свой закон распределения вероятностей и свою функцию распределения вероятностей. Прежде, чем дать определение функции распределения, рассмотрим переменные, которые её определяют. Пусть задано некоторое х – действительное число и получена случайная величина X, при этом (x>X). Требуется определить вероятность того, что случайная величина Х будет меньше этого фиксированного значения х.

Функцией распределения случайной величины Х называется функция F(х), определяющая вероятность того, что случайная величина Х в результате испытания примет значение меньшее значения х, то есть:

F (х) = Р(Х < х ).

(1)

где х – произвольное действительное число.

Случайная величина (непрерывная или дискретная) имеет численные характеристики:

Математическое ожидание М (Х). Эту характеристику можно сравнивать со средним арифметическим наблюдаемых значений случайной величины Х.

Дисперсия D(X). Это характеристика отклонения случайной величины Х от математического ожидания.

Среднее квадратическое отклонение s(Х) для дискретной и непрерывной случайной величины Х – это корень квадратный из ее дисперсии:

(2)

ГЛАВА 2. ДИСКРЕТНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА

Рассмотрим дискретную случайную величину на примере.

Пример 1.

Число появлений герба при трех бросаниях монеты является дискретной случайной величиной Х. Возможные значения числа появлений герба: 0,1,2,3. Следует найти вероятность появления герба в одном испытании.

Решение. Вероятность появления герба в одном испытании равна p=1/2.

Противоположное ему событие: герб не выпал, вероятность этого события равна q=1-p=1/2.

1) Событие 1. «Три раза бросили монету и ни разу герб не выпал». Это сложное событие состоит из появления трёх совместных и независимых элементарных событий: «герб не выпал в одном испытании». Для  события «три раза бросили и ни разу герб не выпал», которое обозначим Р(0), вероятность вычисляется по формуле умножения, для независимых событий:



2) Событие 2. «Три раза бросили монету и один раз герб выпал». Это сложное событие состоит из появления одного из трёх несовместных и независимых событий: «герб  выпал в одном из трёх совместных испытаний». Для  события «три раза бросили монету и один раз герб выпал» вероятность будет состоять из суммы несовместных событий по формуле, где каждое слагаемое вычисляется по формуле для независимых событий:

.

3) Событие 3. «Три раза бросили и два раза выпал герб». Для этого события вероятность события будет состоять из суммы событий:

.

4) Событие 4. «Три раза бросили и все три раза выпал герб». Вероятность этого события совпадает с первым и вычисляется.

.

Здесь: p₁, p₂, p₃ – вероятность выпадения герба в 1, 2, 3 испытаниях.

q₁, q₂, q₃ – вероятность не выпадения герба в 1, 2, 3 испытаниях.

Результаты вычислений вынесены в таблицу 1.

Таблица 1

Событие Х	герб не выпал	герб выпал 1 раз	герб выпал 2 раза	герб выпал 3 раза
хi	0	1	2	3
Вероятность события: Р(хi)= рi

Законом распределения дискретной случайной величины называют соответствие между полученными значениями дискретной случайной величины и их вероятностями. Его можно задать:

1) таблично (рядом распределения);

2) графически;

3) аналитически (в виде формулы).

В примере 1 закон распределения задан в виде ряда распределения (таблицей 1), где представлены все возможные значения х_i и соответствующие им вероятности р_i = Р ( Х = х_i ). При этом вероятности р_i удовлетворяют условию:

,

потому что:

.

где число возможных значений n может быть конечным или бесконечным.

Графическое изображение ряда распределения называется многоугольником распределения. Для его построения возможные значения случайной величины (х_i) откладываются по оси абсцисс, а вероятности (р_i) – по оси ординат. Точки А_i c координатами (х_i, р_i) соединяются ломаными линиями.

Функция F(х) для дискретной случайной величины вычисляется по формуле:

,

(3)

где суммирование ведется по всем значениям i, для которых х_i< х.

Пример 2.

Для задачи в примере 1 найти функцию распределения вероятности F(х) этой случайной величины и построить ее. Построить многоугольник распределения.

Решение.

Если х £ 0, то F(х) = Р ( Х < х ) = 0.

Если 0 < х £ 1, то F(х) = Р ( Х < х ) = 1/8.

Если 1 < х £ 2, то F(х) = Р ( Х < х ) = 1/8 + 3/8 = 0,5.

Если 2 < х £ 3, то F(х) = Р ( Х < х ) = 1/8 + 3/8 + 3/8 = 7/8.

Если х > 3, то F(х) = Р ( Х < х ) = 1/8 + 3/8 + 3/8 + 1/8 = 1.

В таблицу 2 внесены значения функции распределения вероятности F(х) случайной величины – х.

 

Таблица 2.

№	1	2	3	4	5
хi	0	1	2	3	>3
функция распределения F(х)	0	0,125	0,5	0,875	1

Для построения многоугольника распределения значения случайной величины х переписаны в другой форме из таблицы 1 в таблицу 3.

Таблица 3

№	1	2	3	4
хi	0	1	2	3
Ряд распределения Р(хi)= рi	0,125	0,375	0,375	0,125

 

Многоугольник распределения и полученная функция распределения вероятности представлены на рис. 1, 2.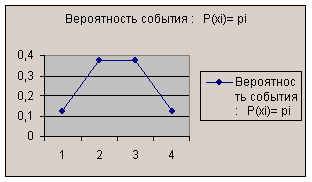



Рис.1. Многоугольник распределения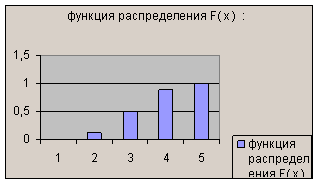

 



Рис.2. Функция распределения

ГЛАВА 3. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН

1) Математическое ожидание М(Х) дискретной случайной величины Х это сумма произведений всех возможных значений величины Х на соответствующие вероятности:

М(Х) = x1· p1 + x2· p2 + … + xn· pn.

(4)

Свойства математического ожидания:

1. 
   Математическое ожидание имеет ту же размерность, что и сама случайная величина.
   
2. 
   Математическое ожидание может быть как положительным, так и отрицательным числом.
   
3. 
   Математическое ожидание постоянной величины С равно этой постоянной. М (С) = С.
   
4. 
   Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий этих величин.
   

М (X + Y + . . . + W) = М (X) + М (Y) + . . . + М (W).

5. 
   Математическое ожидание произведения двух или нескольких взаимно независимых случайных величин равно произведению математических ожиданий этих величин.
   

М (XY) = M(X) × M(Y).

6. 
   Постоянный множитель можно выносить за знак математического ожидания:
   

М(СХ) = С× М(Х).

2) Дисперсия D(X) дискретной случайной величины Х – это математическое ожидание квадрата отклонения случайной величины Х от ее математического ожидания:

D(X) = M [X – M(X)]2.

(5)

Формула (5.5) после возведения в степень и преобразований имеет вид:

D(X) = M (X2) – [M(X)]2.

(6)

Свойства дисперсии:

Дисперсия имеет размерность, равную квадрату размерности случайной величины.

Дисперсия постоянной величины всегда равна нулю: D (С) = 0.

Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: D (СX) = С²×D(X).

Дисперсия алгебраической суммы двух независимых случайных величин равна сумме их дисперсией: D(X +Y) = D(X) + D(Y).

3) Среднее квадратическое отклонениеs(Х) дискретной случайной величины Х определяется формулой (2). Среднее квадратическое отклонение имеет ту же размерность, что и случайная величина.

Случайная величина называется центрированной, если математическое ожидание M(X)=0, и стандартизированной, если M(X)=0 и среднее квадратическое отклонение s = 1.

Рассмотрим на примере вычисление числовых характеристик дискретных случайных величин.

Пример 3.

Найти математическое ожидание М (Х), дисперсию D(Х) и среднее квадратическое отклонение s(Х) дискретной случайной величины Х, заданной законом распределения в таблице 4.

Таблица 4

Х	-5	2	3	4
р	0,4	0,3	0,1	0,2

 

Решение. Математическое ожидание Х вычисляется по формуле (4):

М(Х)= –5× 0,4 + 2× 0,3 + 3× 0,1 + 4× 0,2 = -0,3.

Дисперсия вычисляется по формуле (5.6): D(Х) = М(Х²) – [М(Х)]².

Закон распределения квадрата Х² случайной величины задан в таблице 5.

Таблица 5

Х2	25	4	9	16
р	0,4	0,3	0,1	0,2

Математическое ожидание Х²:

М(Х²) = 25×0,4 + 4×0,3 + 9× 0,1 + 16×0,2 = 15,3.

Искомая дисперсия:

D(Х) = М(Х²) – [М(Х)]² = 15,3 – (– 0,3)2 = 15,21.

Тогда среднее квадратическое отклонение будет:  .























ГЛАВА 4. НЕПРЕРЫВНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА

Если рассматривать случайную величину Х, значения которой заполняют интервал (a,b) и составить перечень всех возможных её значений невозможно, то она называется непрерывной. В результате этого появилась необходимость дать общий способ задания любых типов случайных величин. Для этого вводится функция распределения вероятностей случайной величины. Функция распределения F(х) для непрерывной случайной величины имеет вид:

,

(7)

где: f(х) – функция плотности вероятности вычисляется по формуле:

.

(8)

Функцию распределения F(х) называют интегральным законом распределения, плотность вероятности f(х). называют дифференциальным законом распределения.

Свойства функции распределения F(х):

Свойство 1. Значения функции распределения F(х) принадлежат отрезку [0, 1]:

0 £ F(х) £ 1.

Свойство 2. F(х) – неубывающая функция:

F ( х₁ ) £ F( х₂ ), если х₁< х₂.

Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале (a, b) равна приращению функции распределения на этом интервале:

Р (а £ Х
Свойство 3.Если возможные значения случайной величины принадлежат интервалу (a,b), то:

F(x)=0 при x£a;

F(x)=1 при x³b.

Следствие 2. Если возможные значения непрерывной случайной величины расположены на всей оси х, то:

;  .

Свойства плотности вероятности f(х) :

Свойство 1. Плотность вероятности не может быть отрицательной: f(х) ³ 0.

Свойство 2.

.

(9)

ГЛАВА 5. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

Математическое ожидание

Математическое ожидание непрерывной случайной величины Х:

.

(10)

f(х) – плотность вероятности распределения случайной величины Х.

Дисперсия

Дисперсия непрерывной случайной величины Х:

	.	(11)
	.	(12)

Среднее квадратическое отклонение

5.1 Некоторые частные распределения непрерывной случайной величины

На практике приходится при решении задач сталкиваться с различными распределениями непрерывных случайных величин. Плотность распределения f(x) непрерывной случайной величины называют законом распределения.

Следует рассмотреть некоторые важные для практики распределения случайных величин и соответствующие им числовые характеристики.

Равномерное распределение

Непрерывная случайная величина   называется распределенной равномерно на отрезке [a,b], если её плотность распределения вероятностей постоянна на данном отрезке:

.

(13)

Функция распределения в этом случае функция примет вид:

.

(14)

Числовые характеристики случайной величиныX равномерно распределенной на интервале (a,b):

1. Математическое ожидание по формуле (5.11):

.

2. Дисперсия по формуле (15):



Т .

3. Среднее квадратическое отклонение – s(Х) по формуле (2):



Пример 4. Найти дисперсию и среднее квадратическое отклонение случайной величины   равномерно распределенной на интервале [2; 6].



Решение. Математическое ожидание: .

Дисперсия:        

    .

Среднее квадратическое отклонение:  



Это распределение реализуется, например, в экспериментах, в которых наудачу ставится точка на интервале [a,b], при этом случайная величина X – абсцисса точки.

Вероятность попадания равномерно распределенной непрерывной случайной величины Х на интервале [a,b] определяется по формуле (9).

Примером равномерно распределенной непрерывной случайной величины Х является ошибка при округлении отсчета до ближайшего целого деления шкалы измерительного прибора, проградуированной в некоторых единицах.

Пример 5.

Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляют до ближайшего деления. Найти вероятность того, что ошибка отсчета: а) превысит значение 0,04; б) меньше 0,04.

Решение. Ошибку округления отсчета можно рассматривать как случайную величину Х, которая распределена равномерно в интервале между двумя соседними делениями. Плотность равномерного распределения

,

где (b-a) – длина интервала, в котором заключены возможные значения Х.

Вне этого интервала f (x) = 0. В рассматриваемой задаче длина интервала, в котором заключены возможные значения Х, равна 0,2. Поэтому плотность распределения вероятностей равна:

.

Тогда ошибка отсчета превысит значение 0,04, если она будет заключена в интервале (0,04; 0,2). По формуле (9):

.

Ошибка отсчета меньше 0,04 будет заключена в интервале (0; 0,04) с вероятностью:

.

На рис.3 представлен график функции р(х) случайной величины, равномерно распределенной на промежутке [a;b].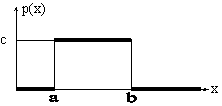



Рис 3. График функции р(х) случайной величины, равномерно распределенной на промежутке [a;b]

Нормальное распределение

Непрерывная случайная величина - x имеет нормальное распределение с параметрами: m, s>0, если плотность распределения вероятностей имеет вид:

(16)

где: m – математическое ожидание, s – среднеквадратическое отклонение.

Нормальное распределение называют еще гауссовским по имени немецкого математика Гаусса. Тот факт, что случайная величина имеет нормальное распределение с параметрами: m, s, обозначают так: N (m,s), где:



Достаточно часто в формулах математическое ожидание обозначают через а. Если случайная величина распределена по закону N(0,1), то она называется нормированной или стандартизированной нормальной величиной. Функция распределения для нее имеет вид:

.

(17)

График плотности изображен на рис 4.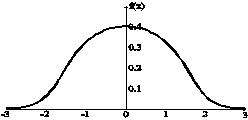



Рис.4. Плотность нормального распределения

Пример 6.

Определение числовых характеристик случайной величины по её плотности рассматривается на примере. Непрерывная случайная величина задана плотностью распределения:

.

Определить вид распределения, найти математическое ожидание M(X) и дисперсию D(X).

Решение. Сравнивая заданную плотность распределения с (16) можно сделать вывод, что задан нормальный закон распределения с m=4. Следовательно, математическое ожидание M(X)=4, дисперсия D(X)=9.

Среднее квадратическое отклонение s=3.

Функция Лапласа, имеющая вид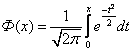

,

связана с функцией нормального распределения (16), соотношением: F₀(x) = Ф(х) + 0,5. Функции Лапласа нечётная. Ф(-x)= -Ф(x). Значения функции Лапласа Ф(х) табулированы и берутся из таблицы по значению х.

Нормальное распределение непрерывной случайной величины играет важную роль в теории вероятностей и при описании реальности, имеет очень широкое распространение в случайных явлениях природы. На практике очень часто встречаются случайные величины, образующиеся именно в результате суммирования многих случайных слагаемых. В частности, анализ ошибок измерения показывает, что они являются суммой разного рода ошибок. Практика показывает, что распределение вероятностей ошибок измерения близко к нормальному закону.

С помощью функции Лапласа можно решать задачи вычисления вероятности попадания в заданный интервал и заданного отклонения нормальной случайной величины.

ГЛАВА 6. ВЕРОЯТНОСТЬ ПОПАДАНИЯ В ЗАДАННЫЙ ИНТЕРВАЛ НОРМАЛЬНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

Если случайная величина Х задана плотностью распределения f(x), то вероятность того, что Х примет значение, принадлежащее заданному интервалу, вычисляется по формуле (9). Подставив в формулу (9) значение плотности распределения из (16) для нормального распределения N(a, s) и сделав ряд преобразований, вероятность того, что Х примет значение, принадлежащее заданному интервалу [x₁, x₂], будет равна:

,

(18)

где: а – математическое ожидание.

Пример 7.

Случайная величина Х распределена по нормальному закону. Математическое ожидание a=60, среднеквадратическое отклонение  =20. Найти вероятность попадания случайной величины Х в заданный интервал (30;90).

Решение. Искомая вероятность вычисляется по формуле (5.18).

Получим: P(30 < X < 90) = Ф((90 – 60) / 20) –Ф((30 – 60)/20) = 2Ф(1,5).

По таблице Приложения 1: Ф(1,5) = 0,4332.

P(30 < X < 90)=2 Ф(1,5) = 2×0,4332 = 0,8664.

Вероятность попадания случайной величины Х в заданный интервал (30; 90) равна:

P(30 < X < 90) = 0,8664.

6.1. Вычисление вероятности заданного отклонения нормальной случайной величины

Задачи вычисления вероятности отклонения нормальной случайной величины от заданного значения связаны с различного рода ошибками (измерения, взвешивания). Ошибки разного рода обозначаются переменной e.

Пусть e – отклонение нормально распределённой случайной величины Х по модулю. Требуется найти вероятность того, что отклонение случайной величины Х от математического ожидания не превысит заданного значения e.

Данная вероятность записывается в виде: P(|X–a| ≤ e). Предполагается, что в формуле (5.18) отрезок [х₁; х₂] симметричен относительно математического ожидания а.

Таким образом: a–х₁=e; х₂–a =e. Отсюда можно выразить границы интервала [х₁; х₂], которые будут иметь вид:

х1=а – e; х2=а + e.

(19)

В правую часть (5.18) подставляются значения х₁, х₂ из (5.19), а выражение в фигурных скобках переписывается в виде двух неравенств:

1) х₁ ≤ X и заменяется в нём х₁ согласно (5.19), получится: а–e ≤ X или а–X ≤ e.

2) X ≤ х₂ , аналогично заменяется х₂, получится: X ≤ а+e или X–a ≤ e.

Тогда (5.18) можно переписать в виде:

P (|X–a| ≤ e) = 2Ф(e/s) = 2Ф(t),

(20)

где t = e/s.

Через функцию Лапласа выражается и функция нормального распределения в общем случае N(a, s):            

.

(21)

Пример 8.

Производится измерение диаметра детали. Случайные ошибки измерения принимаются за случайную величину Х и подчинены нормальному закону с математическим ожиданием а=0, со средним квадратическим отклонение s=1 мм. Найти вероятность того, что измерение будет сделано с ошибкой, не превышающей по абсолютной величине 2 мм.

Решение. Дано: e=2, s=1мм, а=0.

По формуле (5.20): P ( |X–0| ≤ 2) = 2Ф(e/s) = 2Ф(2/1) = 2Ф(2,0).

По таблице Приложения 1 можно найти: Ф (2,0)=0,4772.

Вероятность того, что измерение будет сделано с ошибкой, не превышающей по абсолютной величине 1 мм равна:

P (|X| ≤ e) = 2×0,4772 = 0,9544.

Пример 9.

Случайная величина, распределенная по нормальному закону с параметрами: а=50 и s=15. Найти вероятность того, что отклонение случайной величина от своего математического ожидания – а будет меньше 5, т.е. P(|X–a| <5).

Решение. С учетом (5.18) будем иметь:

P(|X– a| < e)=2Ф(e/s);

P(|X– 50| < 5) = 2Ф(5/15) = 2Ф(0,333) = 2×0,1293 = 0,2586.

Вероятность того, что отклонение случайной величины от своего математического ожидания будет меньше пяти, равна P(|X–a|) < 5 = 0,2586.



ВЫВОД

Методы, средства и законы теории вероятностей и математической статистики на протяжении всех этапов формирования дисциплины, являлись актуальным, какими и остаются вплоть до наших дней. Главный принцип методов, позволивший затронуть столь огромное количество отраслей и сфер знания - универсальность. Их с легкостью можно применять в любой дисциплине, и при этом они не теряют своей силы, остаются справедливыми. Но никогда еще теория вероятностей не была столь востребована, как сегодня. Связано это в первую очередь с невероятными темпами развития и роста вычислительной техники. С каждым годом она становится все сложнее, повышается быстродействие, количество производимых в секунду операций, и все это происходит не без участия математической статистики, которая, в свою помогает оптимизировать работу вычислительных систем и комплексов, повышает точность расчетов, осуществляет прогностическую функцию. Данная работа частично помогает разобраться в азах дисциплины. Знакомит с фундаментальными понятиями, такими как дискретные и непрерывные случайные величины, поясняет разницу между последними. Знакомит с законами их распределения, с дальнейшим применением всех полученных знаний на практике.

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ

1. 
   Зельдович, Я.Б. Высшая математика для начинающих физиков и техников / Я.Б. Зельдович, И.М. Яглом. - М.: Ленанд, 2019. - 512 c
   
2. 
   Лежнёв, А.В. Высшая математика для экономистов: теория пределов и.: Уч. / А.В. Лежнёв. - М.: Магистр, 2019. - 251 c.
   
3. 
   Лобкова, Н.И. Высшая математика для экономистов и менеджеров: Учебное пособие / Н.И. Лобкова, Ю.Д. Максимов, Ю.А. Хватов. - СПб.: Лань, 2018. - 520 c.
   
4. 
   Лурье, И.Г. Высшая математика. Практикум: Учебное пособие / И.Г. Лурье, Т.П. Фунтикова. - М.: Вузовский учебник, 2018. - 256 c.
   
5. 
   Шипачев, В.С. Высшая математика: Учебник / В.С. Шипачев. - М.: Инфра-М, 2018. - 320 c.
   
6. 
   Ячменёв, Л.Т. Высшая математика: Учебник / Л.Т. Ячменёв. - М.: Риор, 2017. - 42 c.
   
7. 
   Крицков, Л.В. Высшая математика в вопросах и ответах: Учебное пособие / Л.В. Крицков; Под ред. В.А. Ильин. - М.: Проспект, 2017. - 176 c.
   
8. 
   Куликова, Е.В. Высшая математика для горных вузов.Т. 1. Аналитическая геометрия и элементы линейной алгебры: Учебное пособие для вузов / Е.В. Куликова. - М.: Горная книга, 2018. - 512 c.
   
9. 
   Малыхин, В.И. Высшая математика: Учебное пособие / В.И. Малыхин. - М.: ИНФРА-М, 2018. - 365 c.
   
10. 
     Хассан, Н.Ш. Высшая математика для гуманитарных направлений: Учебное пособие для бакалавров / Ю.В. Павлюченко, Н.Ш. Хассан, В.И. Михеев; Под общ. ред. Ю.В. Павлюченко. - М.: Юрайт, 2017. - 238 c.
    
11. 
     Шипачев, В.С. Высшая математика. Базовый курс: Учебное пособие для бакалавров / В.С. Шипачев; Под ред. А.Н. Тихонов. - М.: Юрайт, 2018. - 447 c.
    
12. 
    Бугров, Я.С. Высшая математика в 3 т. Т.3 в 2 книгах. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного: Учебник / Я.С. Бугров, С.М. Никольский. - Люберцы: Юрайт, 2016. - 507 c.
    
13. 
    Кастрица, О.А. Высшая математика для экономистов: Учебное пособие / О.А. Кастрица. - М.: Инфра-М, 2018. – 104 с.
    
14. 
    Кремер, Н.Ш. Высшая математика для экономистов. Учебник / Н.Ш. Кремер и др. - М.: Юнити, 2017. - 448 c.
    
15. 
    Седых, И.Ю. Высшая математика для гуманитарных направлений: Учебник и практикум для академического бакалавриата / И.Ю. Седых, Ю.Б. Гребенщиков, А.Ю. Шевелев. - Люберцы: Юрайт, 2016. - 443 c.
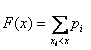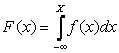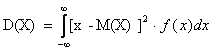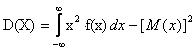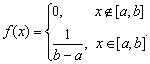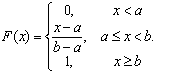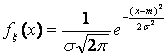
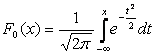