систамный анализ. системный анализ контрольная передел. Введение Задание 1

• Название: Введение Задание 1
• Анкор: систамный анализ
• Дата: 05.04.2023
• Размер: 331 Kb.
• Имя файла: системный анализ контрольная передел.doc
• Тип: Анализ; #1040212
• страница: 2 из 4

П.5.1. Объясните поведение заинтересованных сторон, используя по возможности системные диаграммы.

На рис. 5 изображена схема распределения ограниченных ресурсов (клиентов) между двумя деревенскими поселениями. Допустим, имеем два деревенских поселения: А - с развитым сельскохозяйственным производством, включающим производство продукции сельского хозяйства с растущей тенденцией по годам, ростом поголовья животных и их продуктивности, а также экономических показателей (прибыли, уровня рентабельности). Второе же деревенское поселение В – менее развито, характеризуется отсутствием роста производственных и экономических показателей, упадком жизни, слабой инфраструктурой. В этом случае наблюдается отток населения из второго объекта вследствие низкого уровня жизни и доходов, а также отсутствием перспектив к дальнейшему развитию. Поэтому стечению обстоятельств, в поселок А мигрирует больше населения, что повышает ее репутацию, надежность и успех (положительная обратная связь). Укрепление позиции поселка А привлекает еще больше населения, что усиливает процесс распределения населения в пользу А за счет В. Тем временем сокращение количества населения В усиливается аналогично положительной обратной связью. Такая ситуация приводит к тому, что администрация поселка В теряет веру в свои способности, паникует и «опускает руки», что ведет к еще большей неудаче В.




Уменьшение населения В

Клиенты А





Неудача В

Успех А




Рис. 7. Схема распределения ограниченных ресурсов

Задание 6

Теоретическая часть

Т. 6.1. Кратко охарактеризуйте виды моделей, используемых в исследовании проблем управления и поддержке процесса принятия управленческих решений.

Модель управленческого цикла Шухарта-Деминга (цикл PDCA, то есть Plan-Do-Check-Act, Планируй – Выполняй – Проверяй - Действуй) – модель непрерывного улучшения процессов на системной основе . Включает:

• 
  планирование:
  

1. 
   идентификация (определяем проблему, т.е. обозначаем улучшение качества жизни в селе как проблему);
   
2. 
   анализ проблемы (находим причины, например, экология, низкое качество медицинского обслуживания, плохие социально-экономические условия и т.д., т.е. все то, что влияет на нашу проблему). Необходимо проанализировать, как эти характеристики влияют на проблему, в каких масштабах, и каковы последствия;
   
3. 
   оценка возможностей – сравниваем имеющиеся в нашем распоряжении силы, которые можно направить на решение проблемы. Т.е., каким образом мы можем улучшить экологию – отправить запрос в службу экологического контроля, т.е. обратиться к другой системе. А повысить качество медицинского обслуживания можно своими силами, т.е. совокупностью финансовых, управленческих, нормативных и др. средств;
   
4. 
   планирование необходимых изменений. Например, если стоит вопрос о повышении финансирования больниц, школ, и др., то необходимо составить подробную и обоснованную смету и направить запрос в финансовый отдел департамета;
   

• 
  выполнение – нахождение решения и реализация запланированных мероприятий. Решение принимает руководитель. Глава отдает приказ на составление сметы, анализирует полученный результат, отправляет соответствующий запрос. Получив средства, глава распределяет их на обозначенные нужды;
  
• 
  проверка – сверка результатов с целью, резюмирование. В этом случае должен вестись учет полученных средств, контроль за их использованием. Результат – ремонт, покупка нового оборудования и т.д. должны оправдать поставленную цель и нести пользу;
  
• 
  действие – принятие решения по результатам проверки. Если польза не оправдана, или не полностью оправдана, то необходимо начать процесс сначала – планирование, выполнение, проверка, действие.
  

Кибернетическая модель – модель искусственного интеллекта, основанная на базе экспертных систем. Модель позволяет сформировать дерево целей, определить перечень конкретных задач, условия и составляющие варианта решения. В результате работы формируется вариант деятельности, который будет положен в основу решения.

Кибернетические модели включают системы автоматического регулирования (регистрация пациентов поликлиники для регулирования очередей и пропускной способности специалистов), сложные автоматизированные системы управления.

Алгоритмические модели управления – модели, задающие последовательность управляющих воздействий, выраженных в преобразующей информации. Главная роль в таких моделях отведена человеку, который руководствуется формализованными решениями, выдаваемыми моделью. Ультразвуковое исследование выполняется по определенному алгоритму, в ходе которого выдается формализованная графическая и математическая информация. Исполнитель на основе полученных данных либо проводит углубленное исследование органа, если есть отклонения, либо переходит к другому объекту исследования.

Регрессионные модели с одним уравнением.

В этих моделях исследуется причинная взаимосвязь, т. е. изменения одной переменной в зависимости от изменения других переменных. Зависимая (эндогенная, результирующая, объясняемая) переменная характеризует результат функционирования анализируемой экономической системы. Ее значения формируются внутри процесса функционирования этой системы под воздействием ряда факторов.

Независимые (экзогенные, объясняющие) переменные, или регрессоры, описывают функционирование изучаемой экономической системы, задаются как бы «извне», их изменения являются причиной изменения зависимой переменной.

Например, одним из факторов, влияющих на объем продаж некоторого товара, является его цена. При изучении этой взаимосвязи объем продаж рассматривается как зависимая (эндогенная) переменная, а цена товара – экзогенная переменная, значение которой в какой-то мере определяет объем продаж, является его «причиной».

  Регрессионный анализ занимает центральное место в математико-статистическом инструментарии эконометрики. Он применим, когда изучаемые зависимости:

а) имеют стохастическую природу;

б) выявляются на основании статистического наблюдения за анализируемыми событиями.

На зависимую переменную оказывают влияние не только выделенные в ходе исследования независимые переменные, но и неучтенные факторы, поэтому в эконометрической модели наблюдаемое значение эндогенной (зависимой) переменной можно представить следующим образом:

 



 

Данное уравнение называется уравнением регрессии. Функция f(x,β) называется функцией регрессии, она описывает зависимость среднего значения (условного математического ожидания) зависимой переменной у от значений независимых переменных x = x₁,x₂,...,x_m, ε – случайная компонента (ошибка регрессии, регрессионный остаток), описывает влияние неучтенных в модели факторов, β – параметры модели.

Если пренебречь значением случайной компоненты, то получим  = f(x,β), где   – расчетное (прогнозное) значение эндогенной переменной.

Обычно предполагают, что математическое ожидание (среднее значение) случайной компоненты равно нулю, поэтому   есть среднее значение зависимой переменной при значениях независимых переменных х.

Если в уравнении регрессии присутствует одна независимая переменная, то регрессия называется парной, если в уравнение входит две и более независимых переменных, то регрессия называется множественной.

Если функция регрессии f(x,β) линейна относительно х и β, то данная регрессия называется линейной регрессией, в противном случае регрессия называется нелинейной. Так, функция f(x,β)=β₀+β₁x₁+...+β_mx_m является множественной линейной регрессией.

К нелинейным относятся, в частности, следующие функции парной регрессии: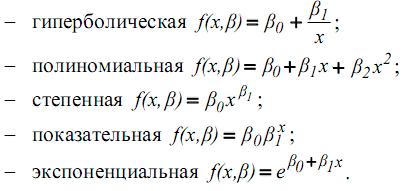



  Основным методом решения задачи нахождения коэффициентов уравнений регрессии является метод наименьших квадратов, разработанный К.Ф. Гауссом.

При построении модели необходимо определить значения параметров β для выбранной функции регрессии, что позволяет в дальнейшем исследовать полученную зависимость и строить прогнозы.

Системы одновременных уравнений.

Эти эконометрические модели описываются системой уравнений, в которые входят как регрессионные уравнения, так и тождества. Причем каждое из регрессионных уравнений в этом случае может включать в себя как независимые переменные, так и зависимые переменные из других уравнений. Это достаточно сложные модели, и их рассмотрение выходит за пределы данного курса. 

Примером такого рода моделей является описание спроса и предложения на рынке, при этом спрос и предложение рассматриваются в зависимости от цены на исследуемый товар, спрос может также зависеть и от уровня дохода потребителей. В равновесии спрос должен быть равен предложению. Таким образом, мы имеем систему трех уравнений с тремя эндогенными, зависимыми переменными: спрос, предложение и цена на товар. 

Модели временных рядов.

В этих моделях рассматривается зависимость эндогенной переменной от времени или от ее значений в прошлые периоды времени. Среди них можно выделить следующие модели:

1. Модели тренда: y(t)=T(t)+ε_t, где у(t) – значение исследуемой переменной в момент времени t, T(t) – некоторая функция, описывающая тренд (тенденцию) изменения переменной y, ε_t – случайная компонента.

2. Модели сезонности: y(t)=S(t)+ε_t, где S(t) – некоторая функция, описывающая сезонные изменения переменной y.

3. Модели тренда и сезонности:

y(t)=T(t)+S(t)+ε_t – аддитивная модель,

y(t)=T(t)∙S(t)+ε_t – мультипликативная модель.

Эти модели описывают сезонные изменения относительно тренда зависимой переменной

4. Адаптивные модели. Позволяют корректировать (адаптировать) модель с получением новой информации. В этих моделях последним, «свежим» наблюдениям придается большее значение, что делает эти модели более гибкими и в ряде случаев повышает качество прогноза.

5. Модели авторегрессии и скользящего среднего (ARIMA-модели). Описывают зависимость значений исследуемого показателя от его значений в предыдущие моменты времени.