Ряды Контрольная. Ряды_контрольная. Задача Найти сумму ряда. Решение. Согласно теореме Виета ( ), уравнение имеет корни
 Скачать 25.4 Kb. Скачать 25.4 Kb.
|
|
Задача № 1. Найти сумму ряда. 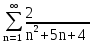 Решение. Согласно теореме Виета ( 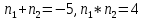 ), уравнение ), уравнение 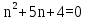 имеет корни имеет корни 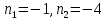 , , 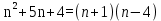 . .Разложим общий член ряда на простейшие дроби: 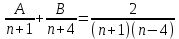 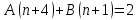 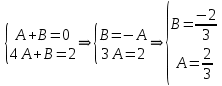 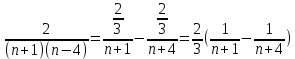 Запишем сумму n первых слагаемых ряда 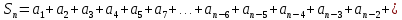 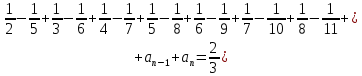 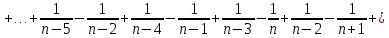 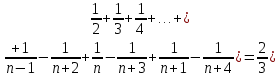 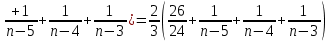 Отсюда  Задача № 2. Используя признак сравнения сходимости, исследовать ряд на сходимость. 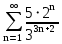 Решение.  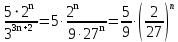 Так как 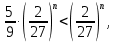 а ряд а ряд 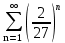 сходится как геометрический ряд с сходится как геометрический ряд с 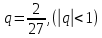 , то по признаку сравнения данный ряд также сходится. , то по признаку сравнения данный ряд также сходится.Задача № 3. Используя предельную форму признака сравнения сходимости, исследовать ряд на сходимость. 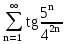 Решение.  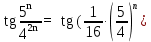 Сравним данный ряд с расходящимся рядом 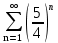 . Предел отношения их общих членов . Предел отношения их общих членов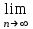 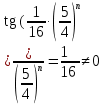 , что означает расходимость исследуемого ряда. , что означает расходимость исследуемого ряда.Задача № 4. Используя признак Даламбера, исследовать ряд на сходимость. 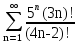 Решение. Вычисляем предел 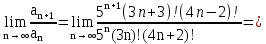 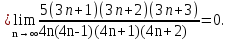 Результат меньше единицы, это говорит о сходимости ряда. Задача № 5. Используя радикальный признак Коши, исследовать ряд на сходимость. 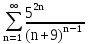 Решение. Так как предел 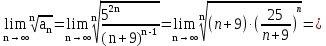 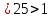 , ряд расходится. , ряд расходится.Задача № 6. Используя интегральный признак Коши, исследовать ряд на сходимость. 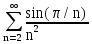 Решение. Вычислим 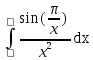 . .Обозначим 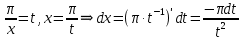 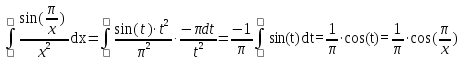 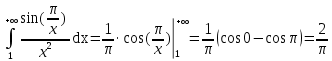 В результате вычисления несобственного интеграла получено, что его значение конечно, это говорит о сходимости интеграла, а следовательно, и ряда. Задача № 7. Исследовать на сходимость знакочередующийся ряд. 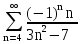 Решение. Легко проверить, что оба условия теоремы Лейбница выполняются для рассматриваемого ряда: члены ряда начиная с первого монотонно убывают по абсолютной величине, т. е. 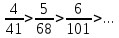 и и 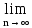 аn = аn = 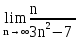 = 0, что говорит о сходимости исследуемого ряда. = 0, что говорит о сходимости исследуемого ряда.Если записать знакоположительный ряд 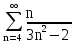 соответствующим данному, то, согласно признаку сравнения, этот ряд будет расходящимся, т. к. соответствующим данному, то, согласно признаку сравнения, этот ряд будет расходящимся, т. к. 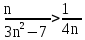 ( как известно, ряд ( как известно, ряд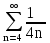 – расходящийся). – расходящийся). Отсюда можно сделать вывод об условной сходимости знакочередующегося ряда 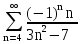 Задача № 8. Найти радиус сходимости и интервал сходимости степенного ряда. 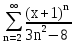 Решение. Пусть R – радиус сходимости ряда. Он может быть вычислен по формуле 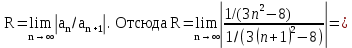 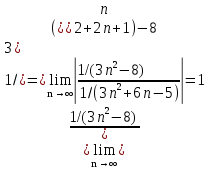 Интервал сходимости находится с помощью неравенства 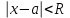 ; подставляя а = -1 и R = 1, находим ; подставляя а = -1 и R = 1, находим . Получается, что . Получается, что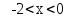 . . Остается выяснить, сходится или расходится ряд в граничных точках интервала сходимости. Для этого в рассматриваемый ряд подставляются x = -2, а затем x = 0 и соответствующие числовые ряды исследуются на сходимость. При x = -2 получится знакочередующийся ряд 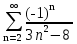 . Оба условия теоремы Лейбница выполняются для него: члены ряда монотонно убывают по абсолютной величине, т. е. . Оба условия теоремы Лейбница выполняются для него: члены ряда монотонно убывают по абсолютной величине, т. е. 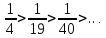 и и 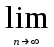 аn = аn = 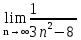 = 0, что говорит о сходимости исследуемого ряда. = 0, что говорит о сходимости исследуемого ряда.При x = 0 получится знакоположительный ряд 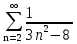 . Он расходящийся, согласно признаку сравнения, т. к. . Он расходящийся, согласно признаку сравнения, т. к.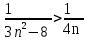 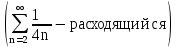 . Следовательно, уточненный интервал сходимости имеет вид . Следовательно, уточненный интервал сходимости имеет вид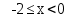 . . |
