КР,ТЕРМОДИНАМИКА,В09,2022. Задача 1 2 Расчёт цикла двигателя внутреннего сгорания (двс) 7 Задача 2 7 Стационарная теплопроводность 19 Задача 3 19
 Скачать 1.34 Mb. Скачать 1.34 Mb.
|
Расчёт цикла двигателя внутреннего сгорания (ДВС)Задача № 2Поршневой двигатель внутреннего сгорания, работающий по циклу Тринклера, со смешанным подводом теплоты (см. рис.1), имеет следующие характеристики цикла: - степень сжатия 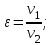 - степень повышения давления 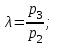 - степень предварительного расширения 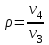 . .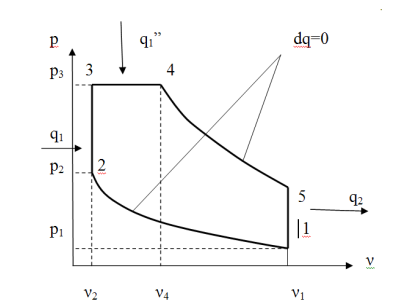 Рис.1 Цикл Тринклера Принимая в качестве рабочего тела 1 кг газовой смеси заданного массового состава с начальными параметрами р1=0,1 МПа и Т1=293 К, определить: - параметры состояния (р, ν, Т) в характерных точках цикла; - для каждого процесса, входящего в цикл: - количество подводимой и отводимой теплоты q; - изменение внутренней энергии ∆u; - изменение энтальпии ∆i; - изменение энтропии ∆s; - совершаемую или затрачиваемую работу l; - работу цикла lц и термический КПД η. Построить цикл в р-ν и Т-s координатах в масштабе. Данные, необходимые для расчетов, выбрать из таблицы 2.1 Таблица 2.1
Примечание: при выполнении расчётов принять значение показателя адиабаты равным: для двухатомных газов 1,4; для трёхатомных 1,3. Решение: Основными термодинамическими процессами являются: - изотермический – при постоянной температуре; - изохорный – при постоянном объеме; - изобарный – при постоянном давлении; - адиабатный – без теплообмена с окружающей средой; - политропный процесс – обобщение всех выше перечисленных процессов. Расчет начинаем с определения молекулярной массы смеси по формуле 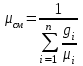 , (2.1) , (2.1)где 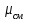 - молекулярная масса смеси, - молекулярная масса смеси, 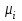 - молекулярная масса i–того компонента смеси, - молекулярная масса i–того компонента смеси, 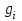 – массовая доля i–того компонента смеси, n – количество компонентов в газовой смеси. – массовая доля i–того компонента смеси, n – количество компонентов в газовой смеси.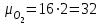 - молекулярная масса кислорода - молекулярная масса кислорода 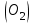 ; ;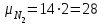 - молекулярная масса азота - молекулярная масса азота 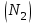 ; ;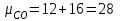 - молекулярная масса оксида углерода - молекулярная масса оксида углерода 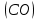 ; ;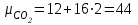 - молекулярная масса углекислого газа - молекулярная масса углекислого газа 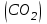 ; ;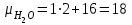 - молекулярная масса водяного пара - молекулярная масса водяного пара 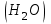 . .Молекулярная масса смеси 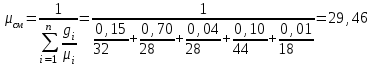 Удельная газовая постоянная смеси: 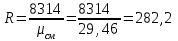 Дж/кг∙К. Дж/кг∙К.Газовые постоянные компонентов смеси 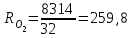 Дж/кг∙К; Дж/кг∙К;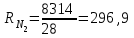 Дж/кг∙К; Дж/кг∙К;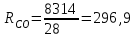 Дж/кг∙К; Дж/кг∙К;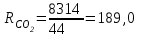 Дж/кг∙К; Дж/кг∙К;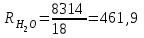 Дж/кг∙К. Дж/кг∙К.Значения удельных теплоемкостей каждого из компонентов смеси при постоянном давлении определяем по формуле 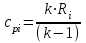 ; (2.2) ; (2.2)где Ri– газовая постоянная компонента; k – показатель адиабаты. 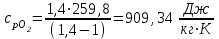 ; ;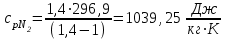 ; ; 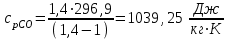 ; ; 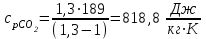 ; ; 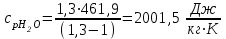 ; ; Значения удельных теплоемкостей каждого из компонентов смеси при постоянном объеме рассчитываем по уравнению 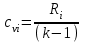 , (2.3) , (2.3)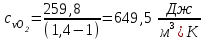 ; ;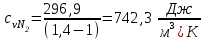 ; ; 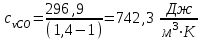 ; ; 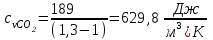 ; ; 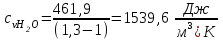 . .Удельную теплоемкость смеси при постоянном давлении 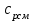 определим по уравнению определим по уравнению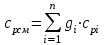 , (2.4) , (2.4)Определяем значение удельной теплоемкости смеси при постоянном давлении 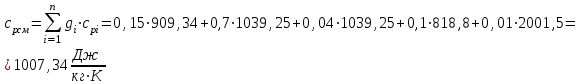 Удельную теплоемкость смеси при постоянном объеме 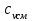 определим по уравнению определим по уравнению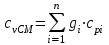 , (2.5) , (2.5)Определяем значение удельной теплоемкости смеси при постоянном объеме 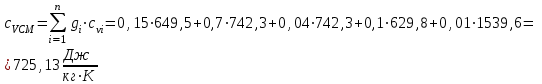 Показатель адиабаты для смеси может быть подсчитан по уравнению 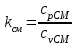 . (2.6) . (2.6)Тогда 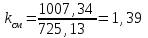 Зная два параметра состояния (температуру и давление), используя уравнение Менделеева - Клапейрона, определим третий параметр состояния – удельный объем рабочего тела в точке 1. 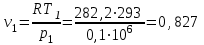 м3/кг. м3/кг.где 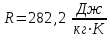 - газовая постоянная смеси - газовая постоянная смесиЗная степень сжатия, определим величину удельного объема после сжатия рабочего тела. Поскольку процесс (1-2) является адиабатным, воспользовавшись уравнениями, описывающими адиабатный процесс, найдем два других параметра состояния рабочего тела в точке 2. Адиабатным процессом называется такой процесс, при котором тепло к ТДС не подводится и не отводится от нее, т. е. система является теплоизолированной (dq = 0). Уравнение состояния политропного процесса 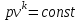 , где k – показатель адиабаты(k = сp/сv> 1). , где k – показатель адиабаты(k = сp/сv> 1).Конечный объем по условию задачи 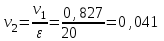 м3/кг. м3/кг.Так как 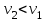 , то характер процесса – сжатие. , то характер процесса – сжатие.Конечное давление определяется из соотношения параметров в политропном процессе: 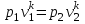 ; ; 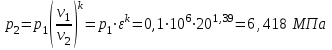 ; ;Соотношения между параметрами в адиабатном процессе и имеют вид: 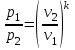 ; ; 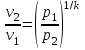 ; ; 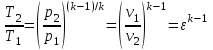 . .Определяем конечную температуру t2 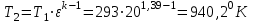 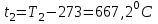 В соответствии с видом цикла, последовательно рассчитаем значения давления, абсолютной температуры и удельного объема в характерных точках цикла. Процесс 2-3 изохорный. Удельный объем v3 в точке 3 равен v2 , так как процесс 2-3 изохорный. Конечный объем 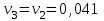 м3/кг. м3/кг.Давление p3 в точке 3 определяем по характеристике цикла 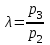 Отсюда 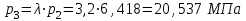 Температура в точке 3 может быть определена из уравнения состояния 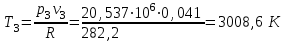 или по уравнению изохорного процесса: 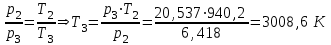 Процесс 3-4 изобарный. Из уравнения состояния идеального газа при р=const находим 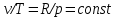 , или , или 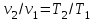 , т. е. в изобарном процессе объем газа пропорционален его абсолютной температуре (закон Гей-Люссака, 1802 г.). , т. е. в изобарном процессе объем газа пропорционален его абсолютной температуре (закон Гей-Люссака, 1802 г.).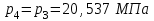 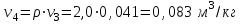 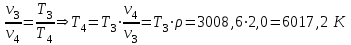 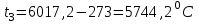 или температура в точке 4 может быть определена из уравнения состояния 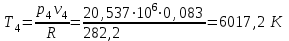 Процесс (4-5) – адиабатное расширение рабочего тела (совершается полезная работа). 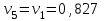 м3/кг. м3/кг.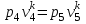 ; ; 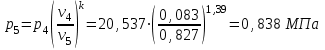 ; ;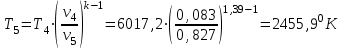 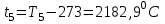 или температура в точке 5 может быть определена из уравнения состояния 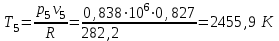 По вычисленным значениям температуры определим значения величины удельной внутренней энергии рабочего тела в характерных точках цикла. 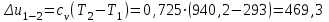 кДж/кг; кДж/кг;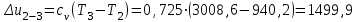 кДж/кг; кДж/кг;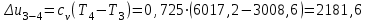 кДж/кг; кДж/кг;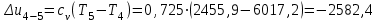 кДж/кг; кДж/кг;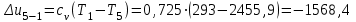 кДж/кг; кДж/кг;Вычислим значения работы и теплоты в процессах, составляющих рассчитываемый цикл. 1-2 адиабатный 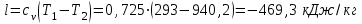 В адиабатном процессе 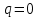 . .2-3 изохорный В изохорном процессе вся теплота расходуется на изменение внутренней энергии: 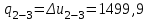 кДж/кг. кДж/кг.Работа в изохорном процессе равна нулю за счет того, что объем остается постоянным: 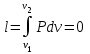 . .3-4 изобарный 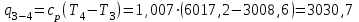 кДж/кг; кДж/кг;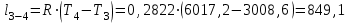  кДж/кг; кДж/кг;4-5 адиабатный 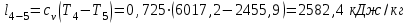 В адиабатном процессе 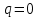 . .5-1 изохорный В изохорном процессе вся теплота расходуется на изменение внутренней энергии: 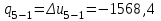 кДж/кг. кДж/кг.Работа в изохорном процессе равна нулю за счет того, что объем остается постоянным: 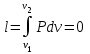 . .Изменение энтальпии ∆i рассчитываем по уравнению 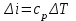 Вычислим значения изменения энтальпий 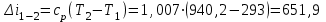 кДж/кг; кДж/кг;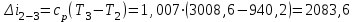 кДж/кг; кДж/кг;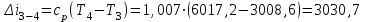 кДж/кг; кДж/кг;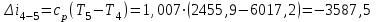 кДж/кг; кДж/кг;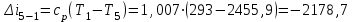 кДж/кг; кДж/кг;Для построения цикла в координатах 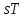 необходимо определить значение энтропии необходимо определить значение энтропии 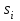 (Дж/кг∙К) для каждой характерной точки цикла по формуле: (Дж/кг∙К) для каждой характерной точки цикла по формуле: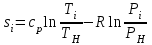 . .Далее получаем: 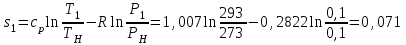 кДж/(кг·К); кДж/(кг·К);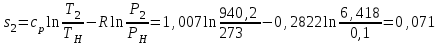 кДж/(кг·К); кДж/(кг·К);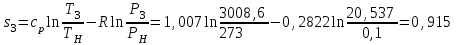 кДж/(кг·К); кДж/(кг·К);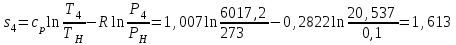 кДж/(кг·К); кДж/(кг·К);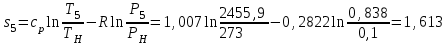 кДж/(кг·К). кДж/(кг·К).Вычислим значения изменения энтропии в термодинамическом цикле: 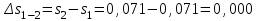 кДж/(кг·К); кДж/(кг·К); 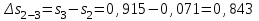 кДж/(кг·К); кДж/(кг·К);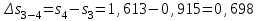 кДж/(кг·К); кДж/(кг·К);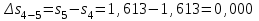 кДж/(кг·К); кДж/(кг·К);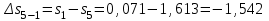 кДж/(кг·К). кДж/(кг·К).Определим суммарные количества подведенной q1 и отведенной q2 теплоты, работу цикла 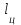 , термический КПД цикла t. , термический КПД цикла t.Подведенная теплота: 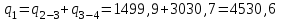 кДж/кг. кДж/кг.Отведенная теплота: 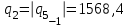 кДж/кг. кДж/кг.Работа цикла: 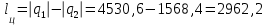 кДж/кг. кДж/кг. Работа цикла lц также может быть рассчитана как сумма работ в отдельных процессах, составляющих цикл. Термический КПД цикла 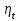 : : 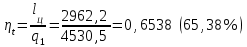 Результаты расчётов сводим в таблицы 2.2 и 2.3. Таблица 2.2
Таблица 2.3
Построим цикл в р-ν и Т-s координатах в масштабе. 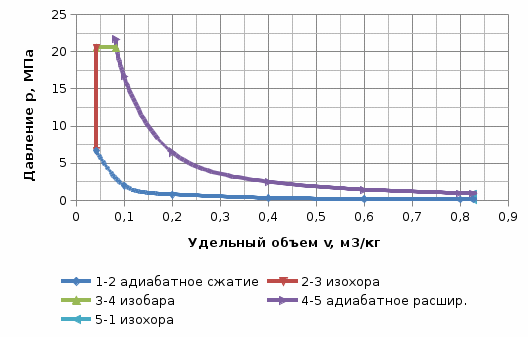 Рис.2. Цикл Тринклера в р-ν координатах 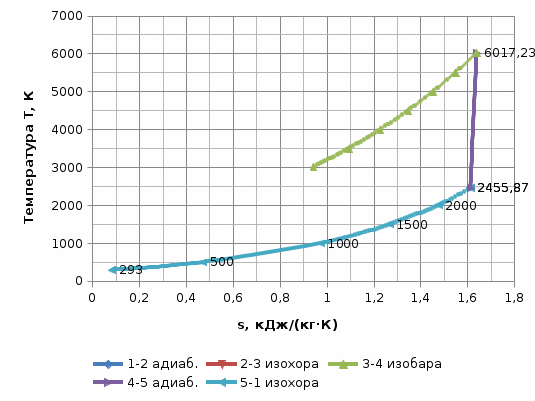 Рис.3. Цикл Тринклера в T-s координатах |
