Главная страница
Навигация по странице:

  • E = L

  • Решение

    		•

    Практические задания по предмету Системный анализ и принятие решений. Задача 1 4 Решение 5 Задача 2 7 Решение 9 Задача 3 10 Решение 11 Задача 4 11 Решение 12 Задача 5 13


    Скачать 385.08 Kb.
    НазваниеЗадача 1 4 Решение 5 Задача 2 7 Решение 9 Задача 3 10 Решение 11 Задача 4 11 Решение 12 Задача 5 13
    АнкорПрактические задания по предмету Системный анализ и принятие решений
    Дата30.04.2023
    Размер385.08 Kb.
    Формат файлаdocx
    Имя файлаPractSAPR_Yushkin_IB06s.docx
    ТипЗадача
    #1098604
    страница5 из 7
    1   2   3   4   5   6   7

    Решение


    Анализируем 9 вариант задачи.

    Для сопоставления рабочей загруженности нескольких предприятий связи создаем модель и выполняем вычисления.

    Результаты вычислений представлены в таблице:

    График
    а
    b
    c
    d
    e

    Первое предприятие
    -0,59012
    -0,60172
    -0,43948
    -0,59688
    -0,58763

    Второе предприятие
    -0,58083
    -0,4927
    -0,62286
    -0,5937
    -0,58982

    Третье предприятие
    -0,58323
    -0,56721
    -0,56276
    -0,49796
    -0,18004

    Построим графические зависимости, поясняющие полученные результаты (рис. 2):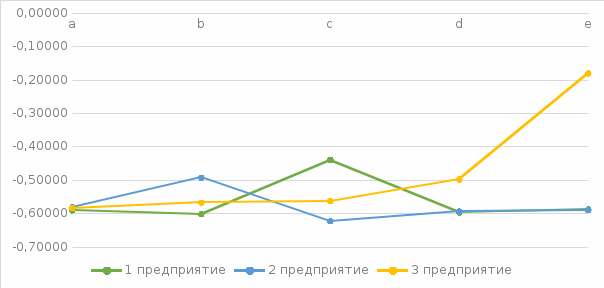



    Рисунок 2

    Задача 6


    Известно, что максимальный размер коробки для почтовой посылки (тары) определяется величиной трех параметров: длиной (L), шириной (W) и высотой (H). Известны ограничения: длина коробки (L) плюс периметр поперечного сечения не превосходят Е (см).

    Это означает, что E = L 2H 2W

    Полагаем, что L = 2H = 2W , L = E / 3

    Требуется:

    1. Найти максимальный размер тары, если известны параметры, представленные в таблице 6- 1.

    2. вычислить максимальное количество упаковочных коробок в 1 м3

    Таблица 6-1

    Номер варианта
    Размер L (см.)
    Параметр Е (см 3)

    9
    56
    26500

    Пояснить полученный результат

    Решение


    По условию имеем L = 2H = 2W. Следовательно можем найти значения H и W: для этого L = 44 делим на 2. Получаем H = W = 28.

    По формуле =(B3+2*D3+2*E3) находим максимальный размер коробки для почтовой посылки (тары) = 168, которое выполняет условие и не превосходит E = 26500.

    Можем найти значение Q: для этого E = 26500 делим на максимальный размер коробки для почтовой посылки (тары) = 168. Получаем Q = 158.

    Результаты вычислений представлены в таблице:

    Номер варианта
    Размер L (см.)
    Параметр Е (см 3)
    Вычислить H (см.)
    Вычислить W (см.)
    Вычислить Q (штуки) в 1 м3

    3
    56
    26500
    28
    28
    158

    В ходе выполнения задачи №6 мы нашли максимальный размер тары = 168 и вычислили максимальное количество упаковочных коробок в 1 м3 = 158.
    1   2   3   4   5   6   7

    написать администратору сайта