метрология стандартизация и сертификация. метрология стандартизация и сертификация КР. Задача 1 Для определения расстояния до места повреждения кабельной линии связи был использован импульсный рефлектометр. С его помощью получено n
 Скачать 337.85 Kb. Скачать 337.85 Kb.
|
Задача № 1 Для определения расстояния до места повреждения кабельной линии связи был использован импульсный рефлектометр. С его помощью получено nрезультатоводнократных измерений (результатов наблюдений) расстояния 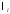 до места повреждения. до места повреждения. Считая, что случайная составляющая погрешности рефлектометра распределена по нормальному закону, определить: 1. Результат измерения с многократными наблюдениями расстояния до места повреждения кабеля 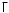 . .2. Оценку среднего квадратического отклонения (СКО) погрешности результата наблюдений (стандартную неопределенность единичного измерения) S; 3. Границы максимальной неопределенность случайной составляющей погрешности результата наблюдений 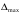 4. Оценку среднего квадратического отклонения погрешности случайной составляющей результата измерения (стандартную неопределенность результата измерения)  ; ;5. Границы доверительного интервала (расширенную неопределенность) для результата измерения расстояния до места повреждения 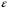 при заданной доверительной вероятности при заданной доверительной вероятности 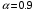 ; ;6. Записать результат измерения расстояния до места повреждения в соответствии с нормативными документами. 7. Систематическую составляющую погрешности измерения рефлектометра 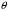 , если после обнаружения места повреждения было установлено. что действительное расстояние до него составляло , если после обнаружения места повреждения было установлено. что действительное расстояние до него составляло 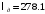 метров. Сравните ее с доверительным интервалом случайной составляющей погрешности результата измерения, и сделать вывод; метров. Сравните ее с доверительным интервалом случайной составляющей погрешности результата измерения, и сделать вывод;8.Предложить способ уменьшения оценки СКО случайной составляющей погрешности результата измерения в 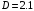 раз. раз.Исходные данные контрольного задания определяют в соответствии с табл. 1.1, 1.2 и 1.3 по номеру варианта MN. Во второй строке табл. 1.1 и 1.2, обозначенной буквой i , указаны номера результатов однократных измерений (наблюдений) 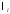 , которые входят в качестве исходных данных в соответствующий вариант контрольного задания. Таким образом, число единичных измерений , которые входят в качестве исходных данных в соответствующий вариант контрольного задания. Таким образом, число единичных измерений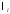 и их числовые значения определяются обеими цифрами пароля (MN). и их числовые значения определяются обеими цифрами пароля (MN).
Таблица 1.3 1. Результат измерения с многократными наблюдениями расстояния до места повреждения кабеля 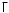 . .Истинное значение 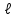 измеренной величины неизвестно, поэтому при числе измерений равное n вместо значения измеренной величины неизвестно, поэтому при числе измерений равное n вместо значения 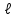 берут наиболее достоверное значение – среднее арифметическое, которое вычисляется по формуле: берут наиболее достоверное значение – среднее арифметическое, которое вычисляется по формуле: 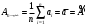 , [3.С.67, ф.(4.6)] , [3.С.67, ф.(4.6)]Для данного случая формула будет выглядеть так: 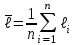 , ,где n – число наблюдений, i – номер наблюдения, 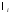 - результат единичного измерения. - результат единичного измерения.После подстановки числовых значений получаем: 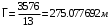 Критерием округления является в дальнейшем посчитанный доверительный интервал, с помощью которого представим результат измерения, у которой имеется два знака после запятой. 2. Оценку среднего квадратического отклонения (СКО) погрешности результата наблюдений (стандартную неопределенность единичного измерения) S; Для расчёта оценки среднего квадратического отклонения погрешности результата наблюдений (стандартной неопределенности единичного измерения) Sнеобходима формула: 2.13 на странице 42 учебника [2]. 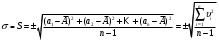 , [2.С.42, ф.(2.13)] , [2.С.42, ф.(2.13)]где 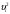 - отклонение результата единичного измерения - отклонение результата единичного измерения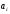 от среднего значения от среднего значения 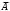 , ,n- число наблюдений 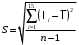 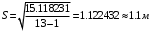 Вычислим погрешность округления: 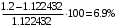 Погрешность округления превышает 5%, следовательно, округление в большую сторону до двух значащих чисел не верное. 3. Границы максимальной неопределенность случайной составляющей погрешности результата наблюдений 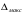 . .Максимальная погрешность результата наблюдений 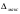 или предельно допустимая погрешность определяется по формуле: или предельно допустимая погрешность определяется по формуле: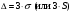 [2.С.43]. [2.С.43].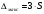 ; ; где Sоценка среднего квадратического отклонения (СКО) погрешности результата наблюдений (стандартная неопределенность единичного измерения). 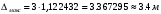 Вычислим погрешность округления: 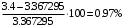 Погрешность округления не превышает 5%, следовательно, округление в большую сторону верное. 4. Оценку среднего квадратического отклонения погрешности случайной составляющей результата измерения (стандартную неопределенность результата измерения)  ; ;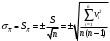 , [2.С.43, ф.(2.14)] , [2.С.43, ф.(2.14)]где 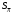 - оценка среднего квадратического отклонения погрешности случайной составляющей результата измерения (стандартная неопределенность результата измерения) - оценка среднего квадратического отклонения погрешности случайной составляющей результата измерения (стандартная неопределенность результата измерения)Для данного случая 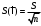 , после подстановки числовых значений получаем , после подстановки числовых значений получаем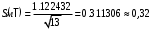 Вычислим погрешность округления: 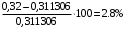 Погрешность округления не превышает 5%, следовательно, округление верное. 5. Границы доверительного интервала (расширенную неопределенность) для результата измерения расстояния до места повреждения 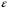 при заданной доверительной вероятности при заданной доверительной вероятности 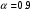 ; ;Доверительный интервал – интервал, в который попадает результат измерения с заданной вероятностью P. Этот интервал рассматривается как допустимое значение погрешности измерения величины. Для расчета доверительного интервала необходима формула: 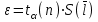 , [3.С.72 ф.4.28] , [3.С.72 ф.4.28]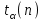 - коэффициент распределения Стьюдента - коэффициент распределения Стьюдента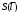 - среднее квадратическое отклонение результата измерения - среднее квадратическое отклонение результата измеренияИз условия задачи 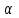 =0,9, значит =0,9, значит 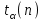 =1.78 [приложение II учебника [1] страница 413]. =1.78 [приложение II учебника [1] страница 413].Доверительный интервал 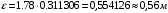 Вычислим погрешность округления: 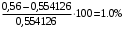 Погрешность округления не превышает 5%, следовательно, округление верное. 6. Запишем результат измерения расстояния до места повреждения в соответствии с нормативными документами (МИ 1317-2004): 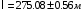 ; ; 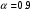 , ,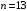 , условия измерения нормальные. , условия измерения нормальные.7. Систематическую составляющую погрешности измерения рефлектометра 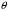 , если после обнаружения места повреждения было установлено. что действительное расстояние до него составляло , если после обнаружения места повреждения было установлено. что действительное расстояние до него составляло 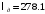 метров. Сравним ее с доверительным интервалом случайной составляющей погрешности результата измерения, и сделать вывод; метров. Сравним ее с доверительным интервалом случайной составляющей погрешности результата измерения, и сделать вывод;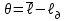 ,[4. Контрольное задание. Указания к заданию 1 контрольной работы]. ,[4. Контрольное задание. Указания к заданию 1 контрольной работы]. где 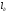 - действительное значение расстояния до места повреждения - действительное значение расстояния до места повреждения - результат измерения расстояния до места повреждения - результат измерения расстояния до места повреждения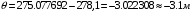 Вычислим погрешность округления: 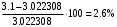 Погрешность округления не превышает 5%, следовательно округление до двух значащих цифр верное. 8.Предложить способ уменьшения оценки СКО случайной составляющей погрешности результата измерения в 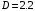 раз. раз.При выполнении задания считаем, что результаты наблюдений распределены по нормальному закону. Точечная оценка дисперсии для результата наблюдений (квадрат СКО результата наблюдений) S2 при большом числе наблюдений (в пределе при n→ к бесконечности) стремится к постоянной величине – дисперсии результата наблюдений σ2 [3.С.71]. Известно [1.С.71, ф. 4.24], что оценка СКО результата измерений зависит от СКО результата наблюдений и числа наблюдений 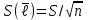 . Из этого выражения видно, что для изменения . Из этого выражения видно, что для изменения 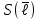 необходимо изменить необходимо изменить 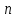 . Отсюда можно получить новое число наблюдений, которое позволит уменьшить . Отсюда можно получить новое число наблюдений, которое позволит уменьшить 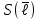 в заданное число D раз. в заданное число D раз.Из этих рассуждений можно получить формулу для вычисления числа наблюдений, необходимого для уменьшения 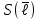 в заданное число D раз: в заданное число D раз: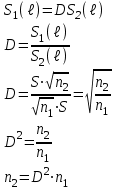 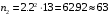 Для уменьшения оценки СКО 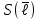 в 2,2 раза необходимо провести 63 наблюдений. в 2,2 раза необходимо провести 63 наблюдений.Задача № 2 При определении вносимого ослабления четырехполюсника необходимо измерить абсолютный уровень мощности рн, отдаваемой генератором с внутренним сопротивлением Rг и ЭДС E в сопротивление нагрузки Rн(рисунок 2.1). 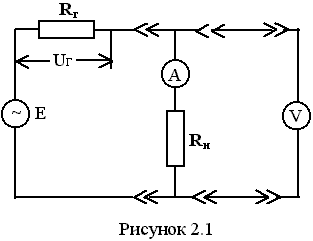 Мощность в нагрузке измеряют с помощью вольтметра V при нормальных условиях измерения. Показания этих приборов и их метрологические характеристики – условное обозначение класса точности и конечное значение шкалы прибора или диапазона измерения приведены в таблице 2.1. В таблице 2.2 приведены: метрологические характеристики измерительного генератора – числовое значение сопротивления Rг и его относительная погрешность Rг; сопротивления нагрузки – значения сопротивления Rн и его относительная погрешность Rн. Таблица 2.1
Таблица 2.3
Необходимо определить: 1. Абсолютный уровень напряжения на сопротивлении нагрузки 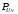 . .2. Абсолютный уровень мощности, выделяемой на внутреннем сопротивлении генератора 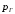 . .3. Оценить границы абсолютной погрешности измерения абсолютных уровней напряжения и мощности, определенных в п.1 и п.2. 4. Оформить результаты измерения абсолютных уровней напряжения и мощности в соответствии с нормативными документами. Решение Абсолютный уровень напряжения на сопротивлении нагрузки: 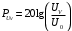 где (где Uо =0,775 В при градировочном сопротивлении равном 600 Ом): 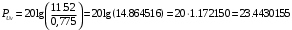 дБ дБ2. Выразим мощность, выделяемую на внутреннем сопротивлении генератора, если уже известно значение протекающего напряжения. Мощность выделяемая на внутреннем сопротивлении генератора: 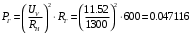 Вт. Вт.Абсолютный уровень мощности, выделяемой на внутреннем сопротивлении генератора 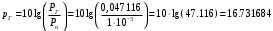 дБ, дБ,3. Оценка границ абсолютной погрешности измерения 3.1 Для оценки границ абсолютной погрешности измерения воспользуемся выражением для оценки погрешности косвенного измерения:  , [2.С.47] , [2.С.47]где А является функцией нескольких переменных. При измерении абсолютного уровня напряжения на сопротивлении нагрузки: 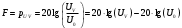 Вычисляем производные, учитывая, что U0 является константой 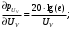 Формула для вычисления абсолютной погрешности результата косвенного измерения: 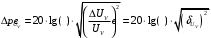 Относительна погрешность вольтметра: 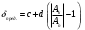 [4, тема 3] [4, тема 3]где Ак – наибольший по модулю из диапазонов измерения; Аn – показания прибора 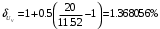 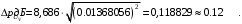 Вычислим погрешность округления: 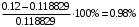 дБ дБПогрешность округления не превышает 5%, следовательно, округление верное. 3.2 Абсолютный уровень мощности, выделяемой на внутреннем сопротивлении генератора рг 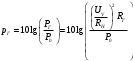 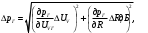 Найдем частные производные функции рГ по всем аргументам по отдельности для простоты оформления а затем подставим в формулу: 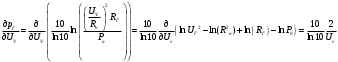 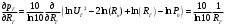 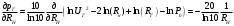 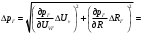 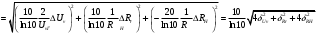 Подставим значения в полученную формулу: 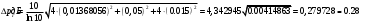 Вычислим погрешность округления: (0,28-0,279728)*100/0,279728=0,1% Погрешность округления не превышает 5%, следовательно, округление верное. 4. Оформим результаты измерения абсолютных уровней напряжения и мощности согласно с нормативными документами: рUV =23.44±0,12, дБ; P=0.997; условия измерения нормальные. рГ =16.73 ±0,28 дБ; P=0.997; условия измерения нормальные. Задача № 3 На рисунке 3.1 показаны осциллограммы периодических сигналов, которые наблюдали на выходе исследуемого устройства . 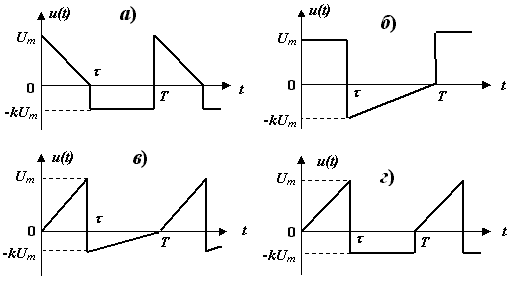 рис. 3.1 Требуется найти: Аналитическое описание исследуемого сигнала. Пиковое (Um), среднее (Uср ), средневыпрямленное (Uср.в) и среднеквадратическое (U) значения напряжения выходного сигнала заданной Вам формы. Пиковое ( 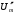 ), среднее ( ), среднее (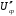 ), средневыпрямленное ( ), средневыпрямленное (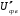 ) и среднеквадратическое ( ) и среднеквадратическое (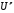 ) значения напряжения переменной составляющей заданного выходного сигнала. ) значения напряжения переменной составляющей заданного выходного сигнала.Коэффициенты амплитуды (Ka, 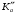 ), формы (Kф, ), формы (Kф,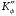 ) и усреднения (Kу, ) и усреднения (Kу, 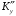 ) всего исследуемого сигнала и его переменной составляющей. ) всего исследуемого сигнала и его переменной составляющей.Показания вольтметров с различными типами преобразователей с закрытым (З) или открытым (О) входом в соответствии с заданием, если вольтметры проградуированы в среднеквадратических значениях для гармонического сигнала. Оценить предел допускаемой относительной погрешности (расширенной неопределенности) показаний вольтметров, определенных в 5 пункте задания, если используемые измерительные приборы имеют класс точности g и конечное значение шкалы (предел измерения) Uкуказанные в таблицах 3.1 и 3.2. Оформить результаты измерений напряжения вольтметрами в соответствии с нормативными документами, если измерения проведены в нормальных условиях. Таблица 3.1
Таблица 3.2
Решение 1. Найдем аналитическое описание сигнала, представленного на рисунке 3.1. Его можно описать следующим образом: 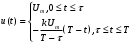 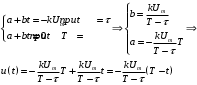 2. Найдем пиковое значение: 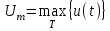 , [3.С.85, ф.(5.1)] , [3.С.85, ф.(5.1)]где Т – период. В данном случае: 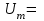 6 В 6 В Найдем среднее значение напряжения, которое можно вычислить по формуле: 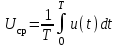 , [3.С.85, ф.(5.2)] , [3.С.85, ф.(5.2)]Подставляя аналитическое выражение данного сигнала, получаем: 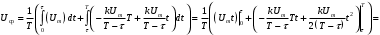 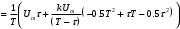 Подставляем численные значения: 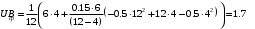 Найдем средневыпрямленное значение напряжения, которое можно вычислить по формуле: 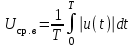 , [3.С.86, ф.(5.3)] , [3.С.86, ф.(5.3)]Подставляя аналитическое выражение данного сигнала, получаем: 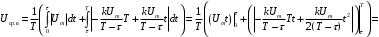 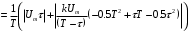 Подставляем численные значения: 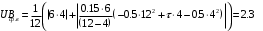 Найдем среднеквадратическое значение напряжения, которое можно вычислить по формуле: 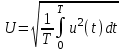 , [3.С.86, ф.(5.4)] , [3.С.86, ф.(5.4)]Подставляя аналитическое выражение данного сигнала, получаем: 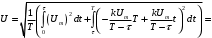 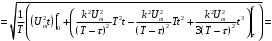 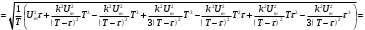 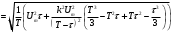 Подставляем численные значения: 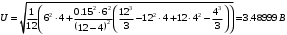 3. Для того, чтобы вычислить пиковое 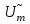 , среднее , среднее 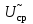 , средневыпрямленное , средневыпрямленное 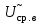 и среднеквадратическое и среднеквадратическое 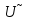 значения напряжения переменной составляющей заданного выходного сигнала, будем использовать все выше приведенные формулы, подставляя в них аналитическое выражение переменной составляющей сигнала значения напряжения переменной составляющей заданного выходного сигнала, будем использовать все выше приведенные формулы, подставляя в них аналитическое выражение переменной составляющей сигнала 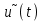 , которое легко найти, вычтя из сигнала u(t) среднее значение напряжения Uср: , которое легко найти, вычтя из сигнала u(t) среднее значение напряжения Uср: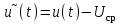 , , Найдем пиковое значение напряжения переменной составляющей выходного сигнала, которое можно вычислить по формуле: 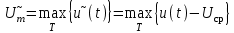 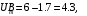 Найдем среднее значение напряжения, которое можно вычислить по формуле: 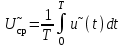 Подставляя аналитическое выражение данного сигнала, получаем: 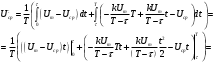 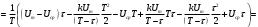 Подставляем численные значения: 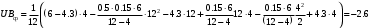 Найдем средневыпрямленное значение напряжения 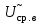 , которое можно вычислить по формуле: , которое можно вычислить по формуле: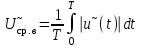 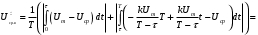 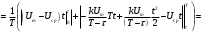 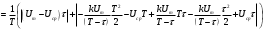 Подставляем численные значения: 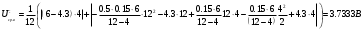 Найдем среднеквадратическое значение напряжения 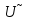 , которое можно вычислить по формуле: , которое можно вычислить по формуле: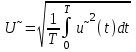 , , Подставляя аналитическое выражение данного сигнала, получаем: 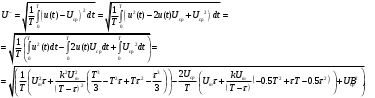 Подставляем численные значения: 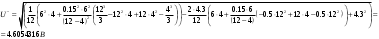 4. Рассчитаем коэффициент амплитуды Ка, формы Кф и усреднения Ку всего исследуемого сигнала по нижеприведенным формулам: Ка= Um/ U Кф= U/ Uср.в[3.С.86 ф.5.5, 5.6, 5.7] Ку= Um/ Uср.в Подставляем численные значения: Ка=6/3.48999=1.7192 Кф=3.48999/2.3=1.51738 Ку=6/2.3= 2.608696 Из приведенных расчетов видно, что соблюдается условие: 1≤ Кф ≤ Ка ≤ Ку [3.С.86] Рассчитаем коэффициент амплитуды 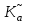 , формы , формы 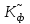 и усреднения и усреднения 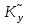 переменной составляющей сигнала: переменной составляющей сигнала:Ка= Um/ U Кф= U/ Uср.в Ку= Um/ Uср.в Подставляем численные значения: Ка=4.3/4.6054316 =0.93368 Кф=4.6054316/3.7333=1.23361 Ку=4.3/3.7333=1.151796 5. Рассчитаем показание UV1 вольтметр с преобразователем средневыпрямленных значений с открытым входом проградуированного в среднеквадратических значениях для гармонического сигнала по формуле: 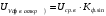 [3.С.90 ф.5.11] [3.С.90 ф.5.11]где Кф.sin= 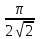 , , 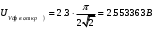 Рассчитаем показание UV2 вольтметр с преобразователем средневыпрямленных значений с закрытым входом. Проградуированного в среднеквадратических значениях для гармонического сигнала с закрытым входом по формуле: 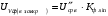 [3.С.90 ф.5.11] [3.С.90 ф.5.11]где Кф.sin= 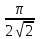 , , 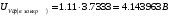 Рассчитаем показание UV3 вольтметр с преобразователем среднеквадратических значений с открытым входом, проградуированного в среднеквадратических значениях для гармонического сигнала с закрытым входом по формуле: 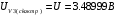 [3.С.90 ф.5.11] [3.С.90 ф.5.11]Рассчитаем показание UV4 пикового вольтметра с закрытым входом, проградуированного в среднеквадратических значениях для гармонического сигнала по формуле: 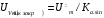 [3.С.90 ф.5.11] [3.С.90 ф.5.11]где Ка.sin= 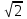 , , 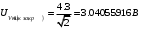 6. Оценим предел допускаемой относительной погрешности (расширенной неопределенности) показаний вольтметров, определенных в 5 пункте задания, если используемые измерительные приборы имеют класс точности γ и конечное значение шкалы (предел измерения) Uк. Сначала оценим абсолютную погрешность: 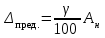 [3.С.32] [3.С.32] где γ – класс точности прибора, Ан – нормирующее значение, которое равно: Ан= Ак=Uк =10В 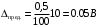 Теперь оценим относительную погрешность измерения: 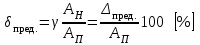 [4. Тема 3. Оценка инструментальной погрешности измерений п.3] [4. Тема 3. Оценка инструментальной погрешности измерений п.3] где Ап – показание прибора. 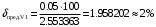 Вычислим погрешность округления: 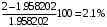 Погрешность округления не превышает 5%, следовательно, округление верное 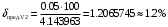 Вычислим погрешность округления: 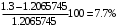 Погрешность округления превышает 5%, следовательно, округление до двух значащих цифр в большую строну нельзя. 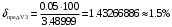 Вычислим погрешность округления: 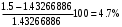 Погрешность округления не превышает 5%, следовательно, округление верное 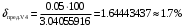 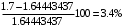 Погрешность округления не превышает 5%, следовательно, округление верное 7. Оформим результаты измерения измерения напряжения вольтметрами согласно МИ1317- 2004: UV1=2,55±0,05, В; Р=0,997; условия измерения нормальные, UV1=2,55В ± 2,0 %; Р=0,997; условия измерения нормальные. UV2=4,14±0,05, В; Р=0,997; условия измерения нормальные, UV2=4,14 В ± 1,2%; Р=0,997; условия измерения нормальные. UV3=3,49±0,05, В; Р=0,997; условия измерения нормальные, UV3=3,49В ± 1,5%; Р=0,997; условия измерения нормальные. UV4=3,04±0,05, В; Р=0,997; условия измерения нормальные, UV4=3,04В ± 1,7%; Р=0,997; условия измерения нормальные. Задача №4 При измерении частоты генератора методом сравнения (рис. 4.1) к входу канала горизонтального отклонения (канала "X") осциллографа приложен гармонический сигнал от генератора образцовой частоты: 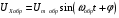 а к входу канала вертикального отклонения (канала "Y") – гармонический сигнал исследуемого генератора: 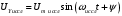 где ω=2πƒ – круговая частота, ƒ – циклическая частота, ψи φ – начальные фазовые углы образцового и исследуемого сигналов соответственно. Измерения проведены в нормальных условиях, границы относительной погрешности частоты образцового генератора 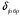 определены с вероятностью P = 0.997. определены с вероятностью P = 0.997.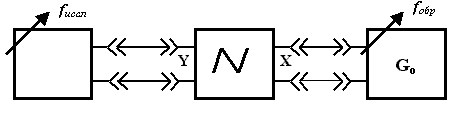 Рисунок 4.1 Задание. 1. Определить по заданным значениям частот сигналов ожидаемое отношение числа точек пересечений фигуры Лиссажу с горизонтальной секущей nгк числу точек пересечений фигуры Лиссажу с вертикальной секущей nв. 2. Построить фигуру Лиссажу, которую можно наблюдать на экране осциллографа при заданных значениях Um обр , ƒобр , Um иссл , ƒиссл , ψ и φ , считая коэффициенты отклонения каналов Y (ko.в) и X (ko.г) одинаковыми и равными 1 В/см . 3. Оценить абсолютную Δƒcр и относительную δƒcр погрешности сравнения частот исследуемого и образцового генераторов, вызванную изменением фигуры Лиссажу, если за время, равное Т секунд, она повторно воспроизводилась 5 раз. 4. Оценить границы абсолютной Δƒиссл и относительной δƒиссл погрешности измерения частоты исследуемого генератора, если известны границы относительной погрешности частоты образцового генератора δ fобр . 5. Записать результат измерения частоты ƒиссл в соответствии с нормативными документами в двух вариантах: 1) с указанием границ абсолютной погрешности; 2) с указанием границ относительной погрешности. Исходные данные для решения приведены в таблицах 4.1 и 4,2. Таблица 4.1 Таблица 4.2
Решение: 1. Для построения фигуры Лиссажу определим кратность частот образцового и исследуемого генераторов[3.с207]: fиссл/fобр=4200/4200=1/1, следовательно ожидаемое число nг/ nв=1/1 При построении фигуры Лиссажу учитываем начальные фазовые углы: φ= 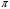 рад и ψ= 0 рад рад и ψ= 0 радТакже учитываем, что координата Х на экране осциллографа пропорциональна мгновенному значению напряжения UХ обр, а координата Y - UY иссл: Х= kо.г* UХ обр Y= kо.в* UY иссл, [из метод.указаний к работе] где kо.ги kо.в – коэффициенты отклонения горизонтального и вертикального каналов осциллографа соответственно они равны 1 В/см . Фигура Лиссажу, которую можно наблюдать на экране осциллографа: 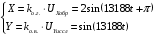 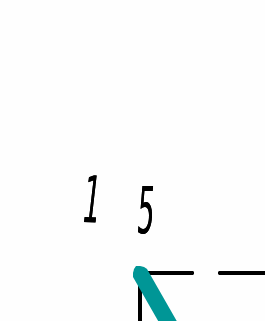 3. Оценить абсолютную Δƒcр и относительную δƒcр погрешности сравнения частот исследуемого и образцового генераторов, вызванную изменением фигуры Лиссажу, если за время, равное Т = 6 секунд, она повторно воспроизводилась 5 раз. 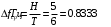 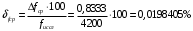 4. Оценить границы абсолютной Δƒиссл и относительной δƒиссл погрешности измерения частоты исследуемого генератора, если известны границы относительной погрешности частоты образцового генератора δ fобр . 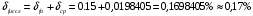 Вычислим погрешность округления: 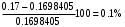 Погрешность округления не превышает 5%, следовательно, округление в большую сторону верное 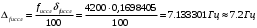 Вычислим погрешность округления: 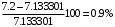 Погрешность округления не превышает 5%, следовательно, округление в большую сторону верное 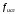 =4200,0±7,2Гц; Р=0,997; условия измерения нормальные, =4200,0±7,2Гц; Р=0,997; условия измерения нормальные,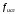 =4200,0Гц ± 0,17 %; Р=0,997; условия измерения нормальные =4200,0Гц ± 0,17 %; Р=0,997; условия измерения нормальные | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

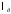 ,м
,м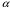
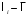 ,м
,м
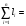 3576
3576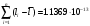
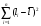 =15.118231
=15.118231