статистика 5 решений. .archстатистика 20.02.19. Задача 1. Имеются следующие данные по фермерским хозяйствам области
 Скачать 70.98 Kb. Скачать 70.98 Kb.
|
|
Задача №1. Имеются следующие данные по фермерским хозяйствам области:
Определить среднюю себестоимость 1 ц. сахарной свеклы в целом по фермерским хозяйствам области. Решение. Определим среднюю себестоимость 1ц. свеклы в целом по фермерским хозяйствам области. Рассчитаем среднюю себестоимость по формуле средней арифметической взвешенной 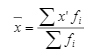 Составим расчетную таблицу
ẋ = 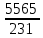 = 24,09 (1 ц./сахарной свеклы руб.) = 24,09 (1 ц./сахарной свеклы руб.)Также себестоимость можно взвесить по валовому сбору.
ẋ = 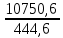 = 24,18 (1 ц./сахарной свеклы руб.) = 24,18 (1 ц./сахарной свеклы руб.)Ответ: средняя себестоимость 1 ц. сахарной свеклы в целом по фермерским хозяйствам области равна 24 руб. Задача №2. Имеются данные о возрастном составе работников фирмы:
Вычислите на основании этих данных показатели вариации (размах, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение). Сделайте выводы. Решение. Данный ряд распределения содержит открытые интервалы. В таких рядах условно принимается величина интервала первой группы равна величине интервала последующей, а величина интервала последней группы равна величине интервала предыдущей. Величина интервала второй группы равна 2, следовательно, и величина первой группы также равна 2. Величина интервала предпоследней группы равна 2, значит и последний интервал будет иметь величину, равную 2. Определим размах вариации как разность между наибольшим и наименьшим значением признака: R = Xmax –Xmin = 31 - 18 = 13 Размах вариации возраста работника равен 13 лет. 2) Средний возраст работника определим по формуле средней арифметической взвешенной. Предварительно определим дискретную величину признака в каждом интервале. Для этого по формуле средней арифметической простой найдём середины интервалов. Среднее значение первого интервала будет равно: Xср. = 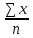 = =  второго – 22, третьего – 24, четвертого – 27, пятого -30 и т. д. Занесём результаты вычислений в таблицу:
Средний размер возраста работника в фирме будет равен 24,8 лет. Xср. = 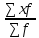 = =  3) Среднее линейное отклонение есть средняя арифметическая из абсолютных отклонений отдельных значений признака от общей средней:  Порядок расчёта среднего линейного отклонения в интервальном ряду распределения следующий: 1. Вычисляется средняя арифметическая взвешенная, как показано в п. 2). 2. Определяются абсолютные отклонения вариант от средней: 3. Полученные отклонения умножаются на частоты: 4. Находится сумма взвешенных отклонений без учёта знака: 5. Сумма взвешенных отклонений делится на сумму частот:  Удобно пользоваться таблицей расчётных данных:
 đ =  Среднее линейное отклонение возраста работника составляет 2,1 года. 4) Дисперсия - это средняя арифметическая квадратов отклонений каждого значения признака от средней арифметической. Расчёт дисперсии в интервальных рядах распределения производится по формуле:  Порядок расчёта дисперсии в этом случае следующий: 1. Определяют среднюю арифметическую взвешенную, как показано в п. 2). 2. Находят отклонения вариант от средней: 3. Возводят в квадрат отклонения каждой варианты от средней: 4. Умножают квадраты отклонений на веса (частоты): 5. Суммируют полученные произведения: 6. Полученная сумма делится на сумму весов (частот): 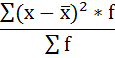 Расчёты оформим в таблицу:
 Ơ2 =  = 7,3 = 7,35) Среднее квадратическое отклонение возраста работника определяется как корень квадратный из дисперсии: Ơ = 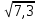 = 2,7 = 2,76) Коэффициент вариации - это отношение среднего квадратического отклонения к средней арифметической:  V =  = 10,9% = 10,9%По величине коэффициента вариации можно судить о степени вариации признаков совокупности. Чем больше его величина, тем больше разброс значений признаков вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя. Ответ: размах вариации равен 13 годам, среднее линейное отклонение составляет 2,1 года, дисперсия равна 7,3 года, среднее квадратическое отклонение равно 2,7 года, коэффициент вариации равен 10,9%, что говорит о небольшом разбросе значений признаков вокруг средней. Задача №3. Имеется выборочное распределение школьников в зависимости от времени, уделяемого ими на подготовку к занятиям в течение недели:
Определите предельную ошибку для числа часов, уделяемых в среднем одним учащимся на подготовку к занятиям, по всей совокупности школьников, учитывая, что наблюдению подвергнуто 50% учеников. Уровень гарантийной вероятности – 0,997. Решение. Для определения границ генеральной средней необходимо вычислить среднюю выборочную
Xср. = 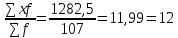  Ơ2 =  = 606,7 = 606,7- при бесповторном отборе: 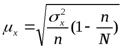 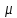 x = x =  Предельная ошибка выборочной средней с вероятностью 0,997 (гарантийный коэффициент t=3) составит ∆ = 1,7*3 = 5,1 ч. Предельная ошибка выборочной доли с вероятностью 0,997 составит (t =3): Δ = t 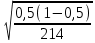 = 3 = 3 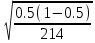 = 0,105 = 0,105Ответ: предельная ошибка для числа часов, уделяемых в среднем одним учащимся на подготовку к занятиям, по всей совокупности школьников, учитывая, что наблюдению подвергнуто 50% учеников составляет 5,1 ч. Задача №4. Имеются следующие данные о производстве продукции:
Используя индексный метод, проведите анализ изменения затрат на произведенную продукцию. Для этого рассчитайте индексы затрат, себестоимости и объема продукции. Сделайте выводы. Определите сумму экономии (перерасхода) от снижения(увеличения) себестоимости продукции. Решение.
1. Индивидуальные индексы : а) себестоимости: Ip = 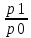 ; ;IpA = 38/40= 0,95 или 95%, себестоимость изделия А уменьшилась на 5% IpБ = 50/50= 1,0 или 100%, себестоимость изделия Б не изменилась IpВ = 63/60= 1,05 или 105%, себестоимость изделия В выросла на 5% б) объем продукции: Iq = 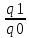 . .IqA = 25/20= 1,25 или 1,25%, объем продукции изделия вырос на 25%. IqБ =18/25= 0,72 или 72%, объем продукции изделия уменьшился на 28%. IqВ = 30/40= 0,75 или 75%, объем продукции изделия уменьшился на 25%. 2.)Общие индексы. Индекс затрат: Ipq = 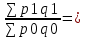 3740/4450 = 0,841 3740/4450 = 0,841 ∆pq = 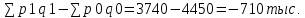 руб. руб.Индекс объема продукции: Iq = 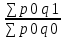 = 3700/4450 = 0,832 = 3700/4450 = 0,832 ∆q =  руб. руб.Индекс себестоимости: Ip =  = 3740/3700 = 1,011 = 3740/3700 = 1,011∆p = 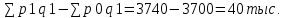 руб. руб. Ответ: индекс затрат составил 0,841 или 84,1%, то есть затраты уменьшились в отчетном периоде на 15,9% или на 710 тыс.руб., индекс объема продукции уменьшился на 16,8% или на 750 тыс.руб. и составил 0,832; индекс себестоимости составил 1,011 или 101,1%, а сумма перерасхода от увеличения себестоимости составила 40 тыс.руб. Задача №5. Рассчитайте среднегодовой темп прироста объема производства на основании следующих данных:
Решение. В общем виде, при наличии базисного и текущего показателя, формула темпа роста выглядит следующим образом: Тр=Птек/Пбаз Здесь Тр – темп роста, Птек – показатель текущего периода, Пкп – показатель базисного периода. Что бы получить более наглядный результат, полученный ответ умножают на 100%, что позволяет выразить темп роста в процентах. Общая формула расчета среднегодового темпа роста выглядит следующим образом: Тр ср = 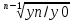 Здесь n– количество месяцев (лет), yn–текущий показатель, y0 – базисный показатель Тр ср = 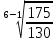 = 1,06 или 106%. = 1,06 или 106%.Ответ: среднегодовой темп прироста объема производства 1,06 или 106%. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
