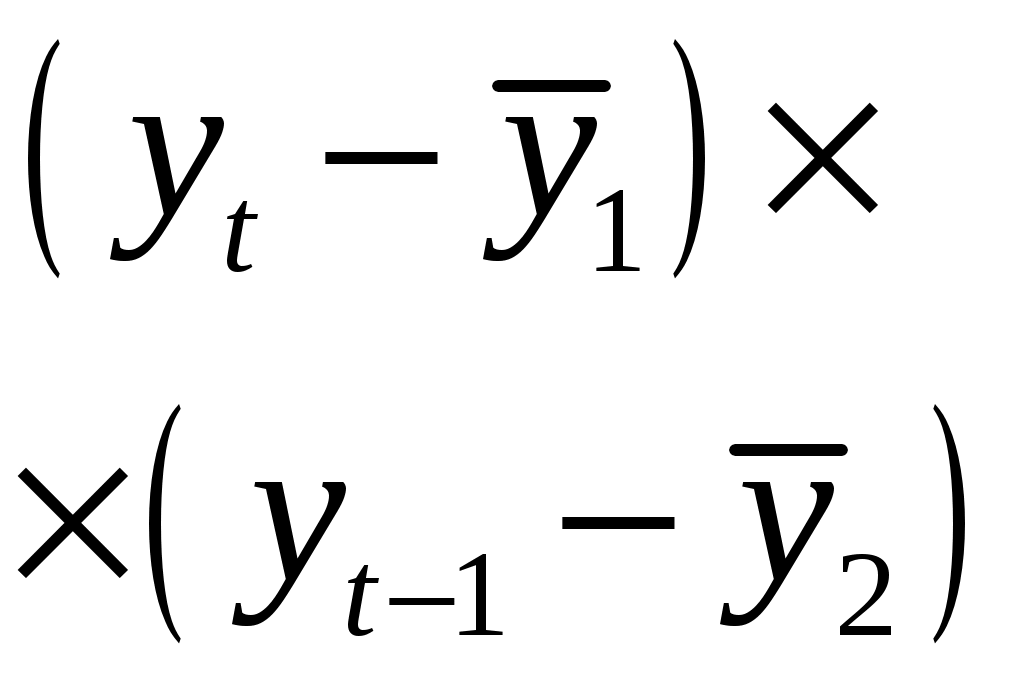Таблица 5
|
|
|
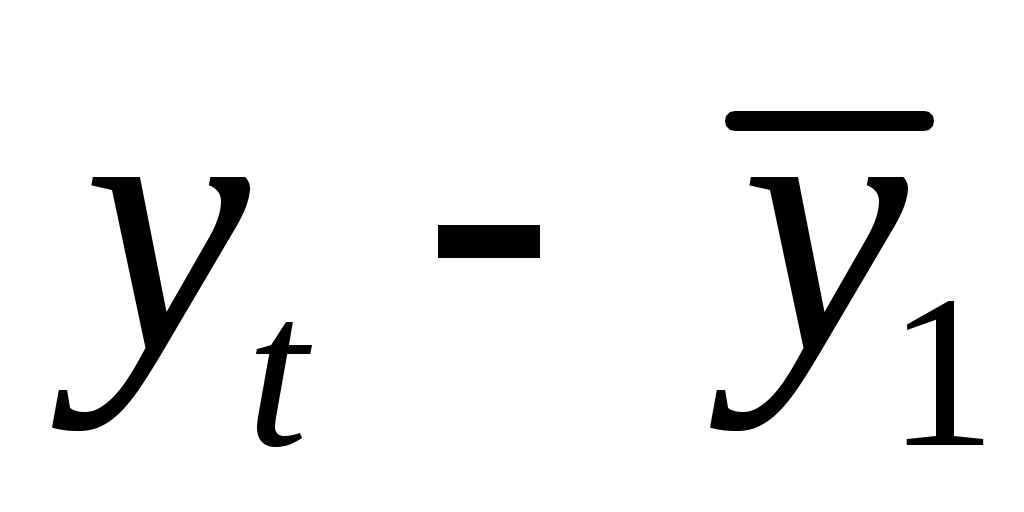
|
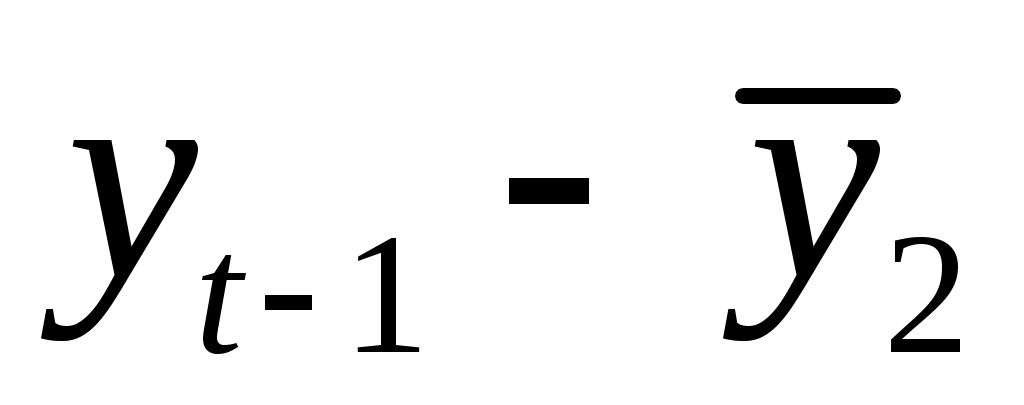
|
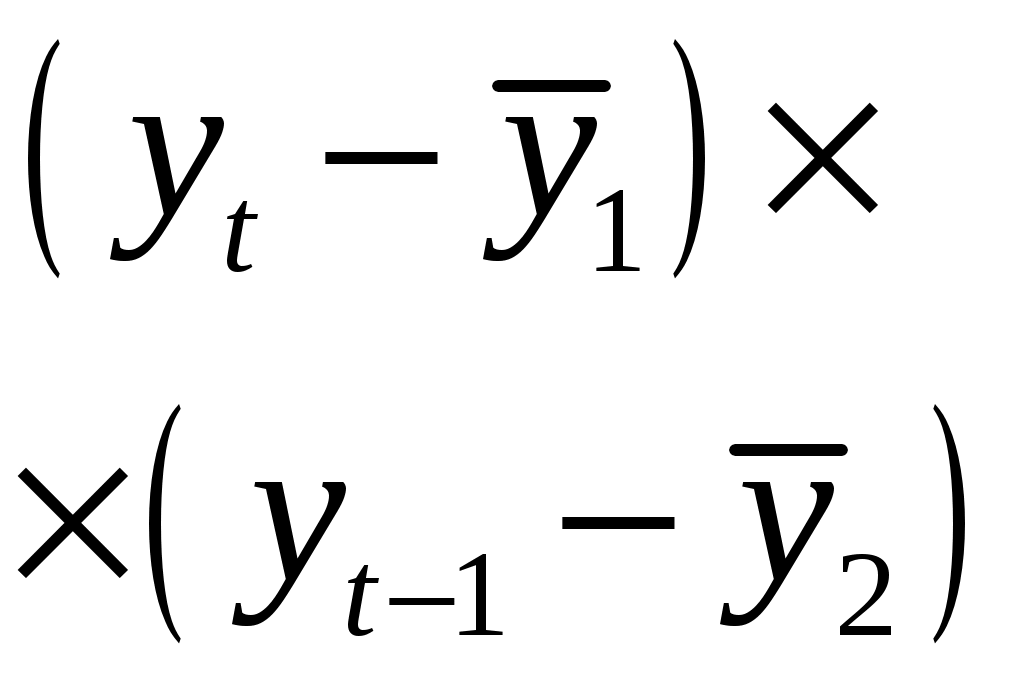
|
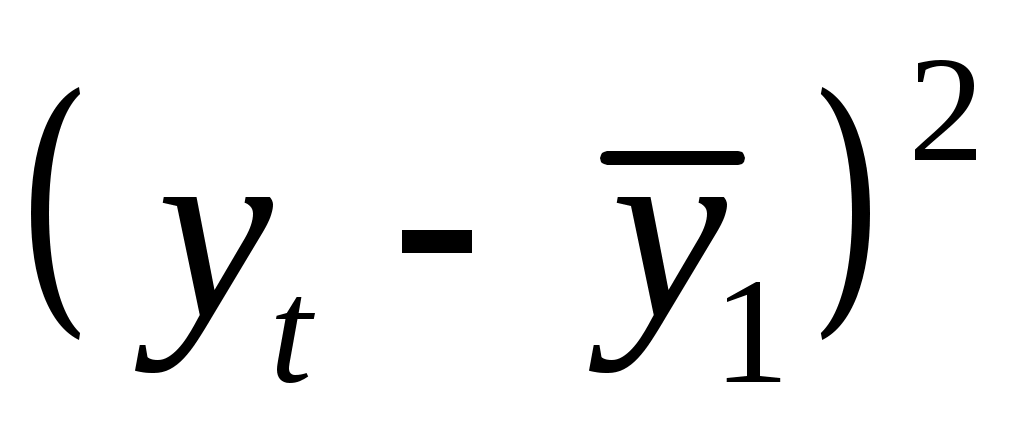
|
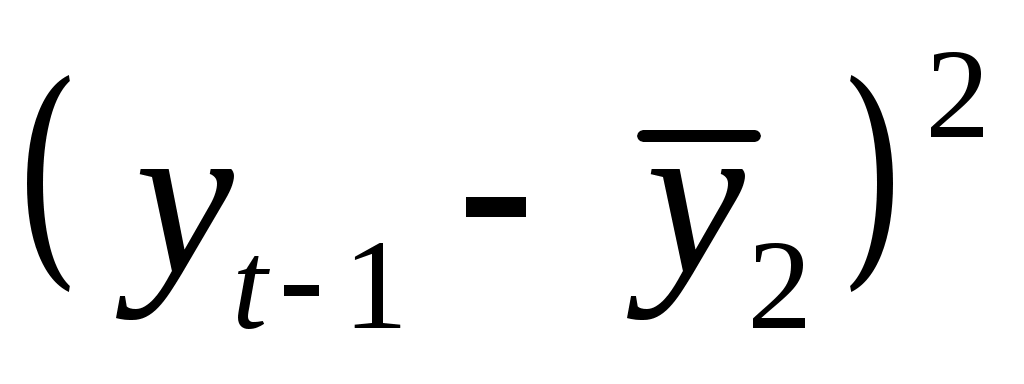
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
1
|
5,5
|
–
|
–
|
–
|
–
|
–
|
–
|
2
|
4,8
|
5,5
|
-2,69
|
-1,61
|
4,3309
|
7,2361
|
2,5921
|
3
|
5,1
|
4,8
|
-2,39
|
-2,31
|
5,5209
|
5,7121
|
5,3361
|
4
|
9
|
5,1
|
1,51
|
-2,01
|
-3,0351
|
2,2801
|
4,0401
|
5
|
7,1
|
9
|
-0,39
|
1,89
|
-0,7371
|
0,1521
|
3,5721
|
6
|
4,9
|
7,1
|
-2,59
|
-0,01
|
0,0259
|
6,7081
|
0,0001
|
7
|
6,1
|
4,9
|
-1,39
|
-2,21
|
3,0719
|
1,9321
|
4,8841
|
8
|
10
|
6,1
|
2,51
|
-1,01
|
-2,5351
|
6,3001
|
1,0201
|
9
|
8,3
|
10
|
0,81
|
2,89
|
2,3409
|
0,6561
|
8,3521
|
10
|
5,4
|
8,3
|
-2,09
|
1,19
|
-2,4871
|
4,3681
|
1,4161
|
11
|
6,4
|
5,4
|
-1,09
|
-1,71
|
1,8639
|
1,1881
|
2,9241
|
12
|
10,9
|
6,4
|
3,41
|
-0,71
|
-2,4211
|
11,6281
|
0,5041
|
13
|
9
|
10,9
|
1,51
|
3,79
|
5,7229
|
2,2801
|
14,3641
|
14
|
6,6
|
9
|
-0,89
|
1,89
|
-1,6821
|
0,7921
|
3,5721
|
15
|
7,5
|
6,6
|
0,01
|
-0,51
|
-0,0051
|
1E-04
|
0,2601
|
16
|
11,2
|
7,5
|
3,71
|
0,39
|
1,4469
|
13,7641
|
0,1521
|
Сумма
|
112,3
|
106,6
|
-0,05
|
-0,05
|
11,4215
|
64,9975
|
52,9895
|
Среднее значение
|
7,49
|
7,11
|
–
|
–
|
–
|
–
|
–
|
Следует заметить, что среднее значение получается путем деления не на 16, а на 15, т.к. у нас теперь на одно наблюдение меньше.
Теперь вычисляем коэффициент автокорреляции первого порядка по формуле :
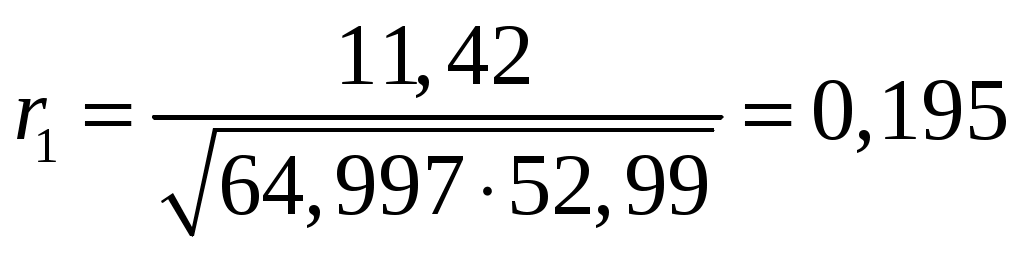
Составляем вспомогательную таблицу для расчета коэффициента автокорреляции второго порядка.
|
 Скачать 1.59 Mb.
Скачать 1.59 Mb.