Математика спец курс. Контрольная работа 1. Задача 1 Парная регрессия и корреляция

• Название: Задача 1 Парная регрессия и корреляция
• Анкор: Математика спец курс
• Дата: 15.10.2021
• Размер: 1.59 Mb.
• Имя файла: Контрольная работа 1.doc
• Тип: Задача; #247994
• страница: 1 из 15

Задача 1 Парная регрессия и корреляция
По территориям региона приводятся данные за 1991 г.

Требуется:

1. 
   Построить линейное уравнение парной регрессии от .
   
2. 
   Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации.
   
3. 
   Оценить статистическую значимость параметров регрессии и корреляции с помощью -критерия Фишера и -критерия Стьюдента.
   
4. 
   Выполнить прогноз заработной платы при прогнозном значении среднедушевого прожиточного минимума , составляющем 107% от среднего уровня.
   
5. 
   Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.
   
6. 
   На одном графике построить исходные данные и теоретическую прямую.
   

Вариант 7

Номер региона	Среднедушевой прожиточный минимум в день одного трудоспособного, руб.,	Среднедневная заработная плата, руб.,
1	75	133
2	78	125
3	81	129
4	93	153
5	86	140
6	77	135
7	83	141
8	94	152
9	88	133
10	99	156
11	80	124
12	112	156

Решение

1. 
   Для расчета параметров уравнения линейной регрессии строим расчетную таблицу 1.
   

Таблица 1

1	75	133	9975	5625	17689	128,942	4,058	3,1
2	78	125	9750	6084	15625	131,612	-6,612	5,3
3	81	129	10449	6561	16641	134,282	-5,282	4,1
4	93	153	14229	8649	23409	144,962	8,038	5,3
5	86	140	12040	7396	19600	138,732	1,268	0,9
6	77	135	10395	5929	18225	130,722	4,278	3,2
7	83	141	11703	6889	19881	136,062	4,938	3,5
8	94	152	14288	8836	23104	145,852	6,148	4
9	88	133	11704	7744	17689	140,512	-7,512	5,6
10	99	156	15444	9801	24336	150,302	5,698	3,7
11	80	124	9920	6400	15376	133,392	-9,392	7,6
12	112	156	17472	12544	24336	161,872	-5,872	3,8
Итого	1046	1677	147369	92458	235911	1677,24	-0,244	50,1
Среднее значение	87,2	139,8	12280,8	7704,8	19659,3	–	–	4,2
	10,05	10,74	–	–	–	–	–	–
	100,96	115,26	–	–	–	–	–	–

;

.

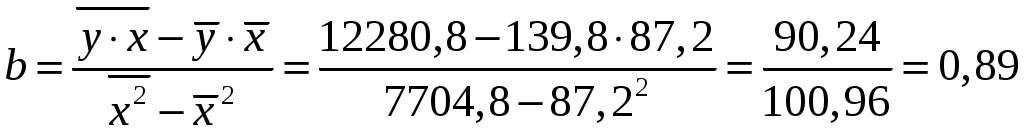Получено уравнение регрессии: .

С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,89 руб.

2. 
   Тесноту линейной связи оценит коэффициент корреляции: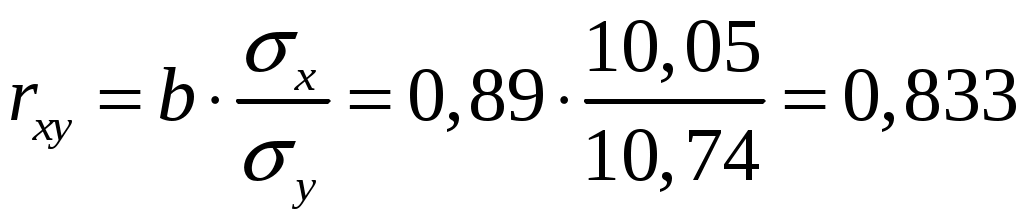
   

; .

Это означает, что 69% вариации заработной платы ( ) объясняется вариацией фактора – среднедушевого прожиточного минимума.

Качество модели определяет средняя ошибка аппроксимации: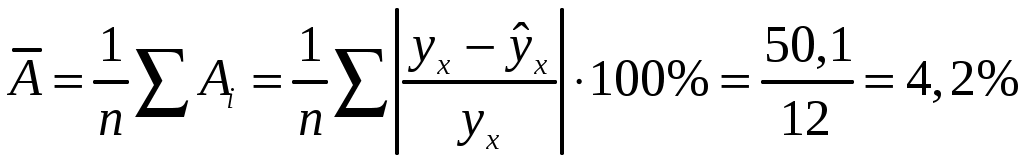

.

Качество построенной модели оценивается как хорошее, так как не превышает 8-10%.

3. 
   Оценку значимости уравнения регрессии в целом проведем с помощью 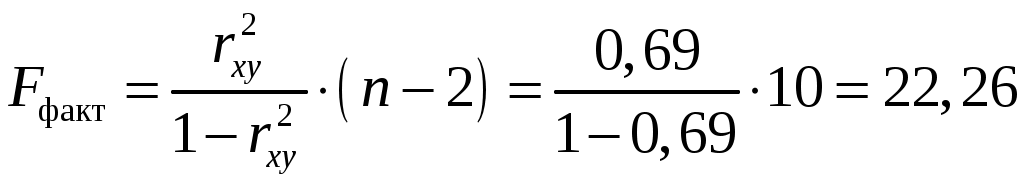-критерия Фишера. Фактическое значение -критерия:
   

.

Табличное значение критерия при пятипроцентном уровне значимости и степенях свободы и составляет . Так как , то уравнение регрессии признается статистически значимым.

Оценку статистической значимости параметров регрессии проведем с помощью -статистики Стьюдента и путем расчета доверительного интервала каждого из показателей.

Табличное значение -критерия для числа степеней свободы и составит .

Определим случайные ошибки , , :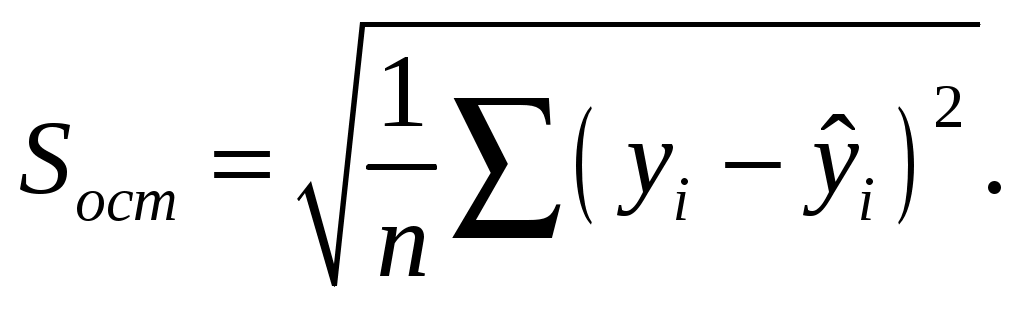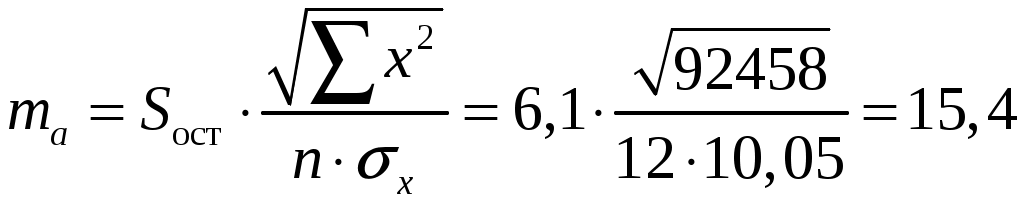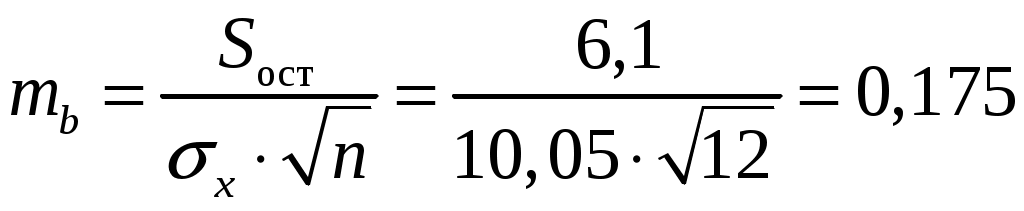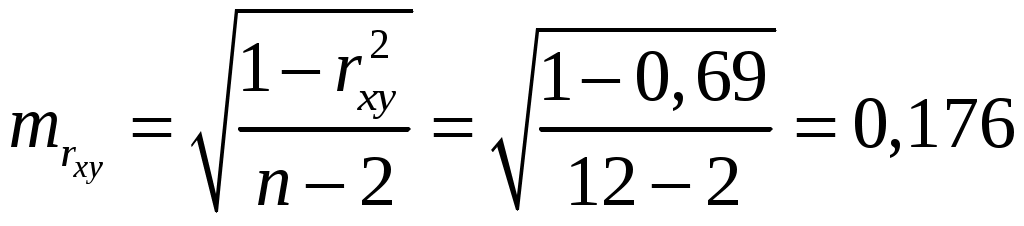

;

;

.

Тогда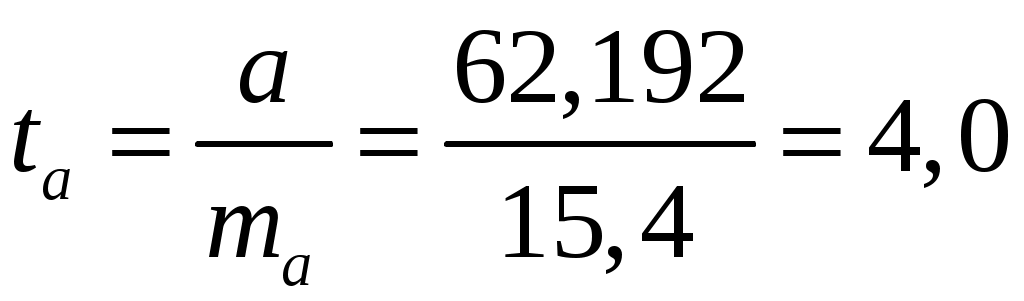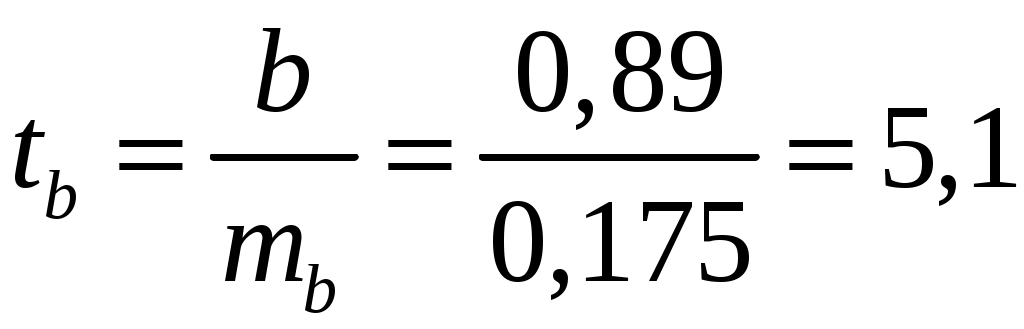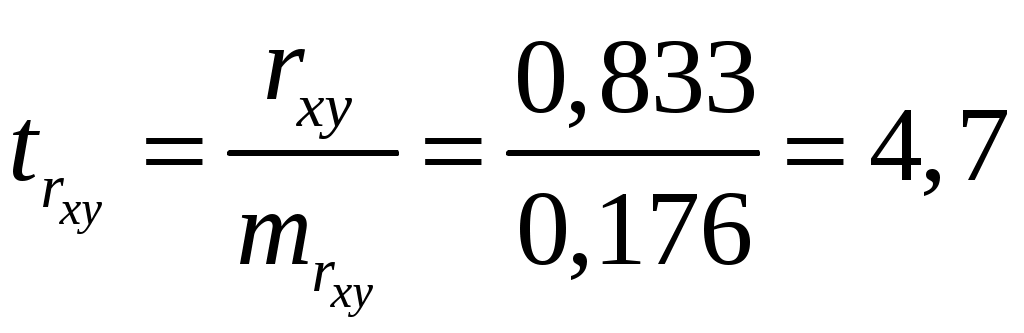

;

;

.

Фактические значения -статистики превосходят табличное значение:

; ; ,

поэтому параметры , и не случайно отличаются от нуля, а статистически значимы.

Рассчитаем доверительные интервалы для параметров регрессии и . Для этого определим предельную ошибку для каждого показателя:

;

.

Доверительные интервалы













Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью параметры и , находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.

4. 
   Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит: руб., тогда прогнозное значение заработной платы составит: руб.
   
   5. 
      Ошибка прогноза составит: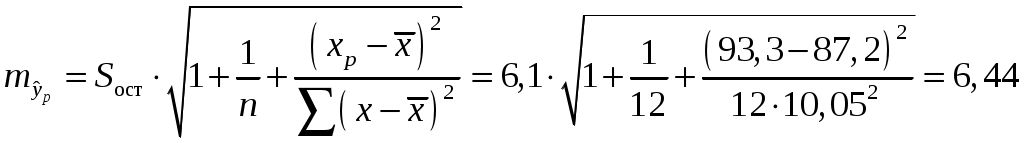
      

.

Предельная ошибка прогноза, которая в случаев не будет превышена, составит:

.

Доверительный интервал прогноза:



руб.;

руб.

Выполненный прогноз среднемесячной заработной платы является надежным ( ) и находится в пределах от 130,27 руб. до 159,59 руб.

6. 
   В заключение решения задачи построим на одном графике исходные данные и теоретическую прямую (рис. 1):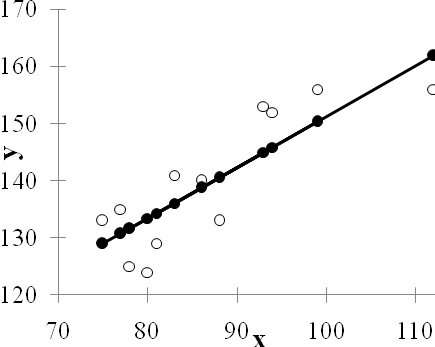
   

Рис. 1. Линия регрессии

Решение типовой задачи в MS Excel
1. Выбираем Сервис→Анализ данных→Регрессия.

2. Заполняем диалоговое окно ввода данных и параметров вывода (рис. 2).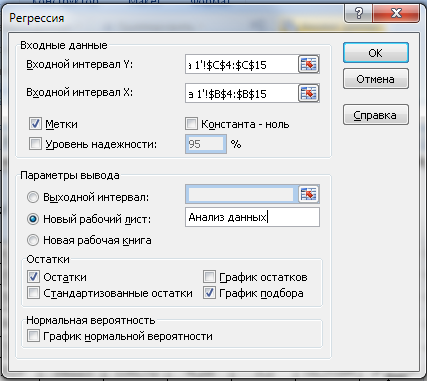

Рис. 2. Окно Регрессия для ввода входных данных
Здесь:

входной интервал Y – диапазон, содержащий данные результативного признака.

входной интервал X – диапазон, содержащий данные признака-фактора.

метки – «флажок», который указывает, содержит ли первая строка названия столбцов.

константа – ноль – «флажок», указывающий на наличие или отсутствие свободного члена в уравнении.

выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона.

новый рабочий лист – можно указать произвольное имя нового листа (или не указывать, тогда результаты выводятся на вновь созданный лист).

Получаем следующие результаты для рассмотренного выше примера (рис. 3).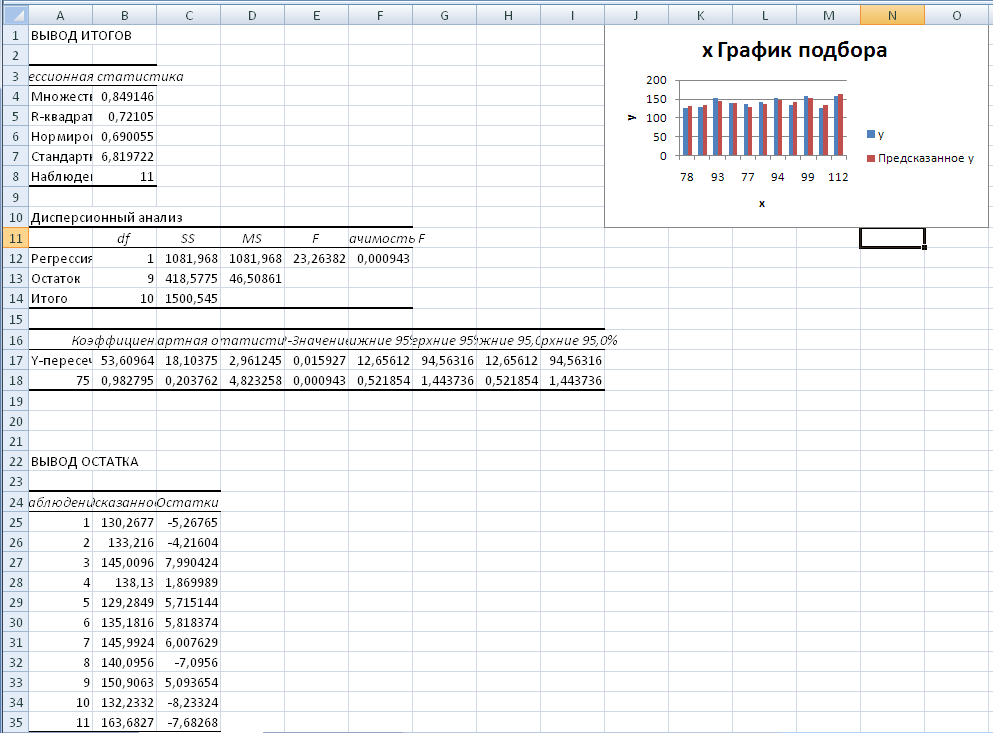

Рис. 3. Окно результатов регрессии
Откуда выписываем, округляя до 4 знаков после запятой и переходя к нашим обозначениям:

Уравнение регрессии (ячейки В17 и В18):

ŷ_x 53,6096  0,9828x.

Коэффициент корреляции (В4):

r_xy 0,8491 .

Коэффициент детерминации (В5):

 0,7210 .

Фактическое значение F-критерия Фишера (Е12):

F  23,2638.

Остаточная дисперсия на одну степень свободы (D13):

 46,5086.

Корень квадратный из остаточной дисперсии (стандартная ошибка) (В7):

S_ост  6,8197.

Стандартные ошибки для параметров регрессии (С17, С18):

m_a 18, 1037, m_b 0,2038.

Фактические значения t-критерия Стьюдента (D17, D18):

t_a 2,9612, t_b 4,8233.

Доверительные интервалы (F17: С18):

12,6561  a^  94,5632,

0,5219  b^  1,4437.

Как видим, найдены все рассмотренные выше параметры и характеристики уравнения регрессии, за исключением средней ошибки аппроксимации (значение t-критерия Стьюдента для коэффициента корреляции совпадает с t_b). Результаты «ручного счета» от машинного отличаются незначительно (отличия связаны с ошибками округления).