Математика спец курс. Контрольная работа 1. Задача 1 Парная регрессия и корреляция
 Скачать 1.59 Mb.
|
|
x1 и x3. Структурные параметры второго уравнения СФМ можно будет определить в два этапа: Первый этап: выразимx1 в данном случае из первого или третьего уравнения ПФМ. Например, из первого уравнения:  .Подстановка данного выражения во второе уравнение ПФМ не решило бы задачу до конца, так как в выражении присутствует x3, которого нет в СФМ. Выразим x3 из третьего уравнения ПФМ:  .Подставим его в выражение x1: 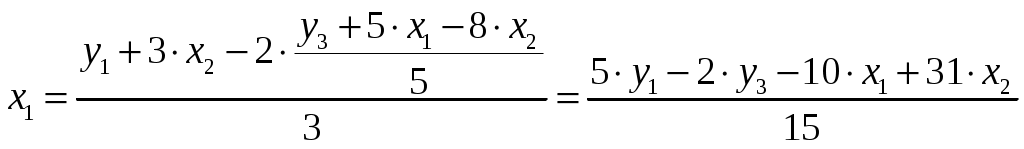 ; .Второй этап: аналогично, чтобы выразить x3 через искомые y1,y3 иx2, заменим в выражении x3 значение x1 на полученное из первого уравнения ПФМ: 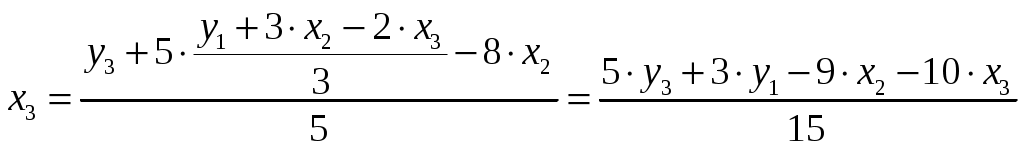 .Следовательно,  .Подставим полученныеx1 и x3 во второе уравнение ПФМ:   – второе уравнение СФМ.Это уравнение можно получить из ПФМ иным путем. Суммируя все уравнения, получим  , ,  Далее из первого и второго уравнений ПФМ исключим x1, домножив первое уравнение на 2, а второе – на (-3) и просуммировав их:  ,  Затем аналогичным путем из полученных уравнений исключаемx3, а именно: 28, , , ,    ;из второго уравнения ПФМ выразим x2, так как его нет в третьем уравнении СФМ:  .Подставим полученное выражение в третье уравнение ПФМ:   – третье уравнение СФМ.Таким образом, СФМ примет вид:  , , . |