Математика спец курс. Контрольная работа 1. Задача 1 Парная регрессия и корреляция
 Скачать 1.59 Mb.
|
Таблица 16
Шаг 4. Определим компоненту  данной модели. Для этого проведем аналитическое выравнивание ряда ( ) с помощью линейного тренда. Результаты аналитического выравнивания следующие: .Подставляя в это уравнение значения  , найдем уровни для каждого момента времени (гр. 5 табл. 16).Шаг 5. Найдем значения уровней ряда, полученные по аддитивной модели. Для этого прибавим к уровням значения сезонной компоненты для соответствующих кварталов (гр. 6 табл. 16).На одном графике отложим фактические значения уровней временного ряда и теоретические, полученные по аддитивной модели. 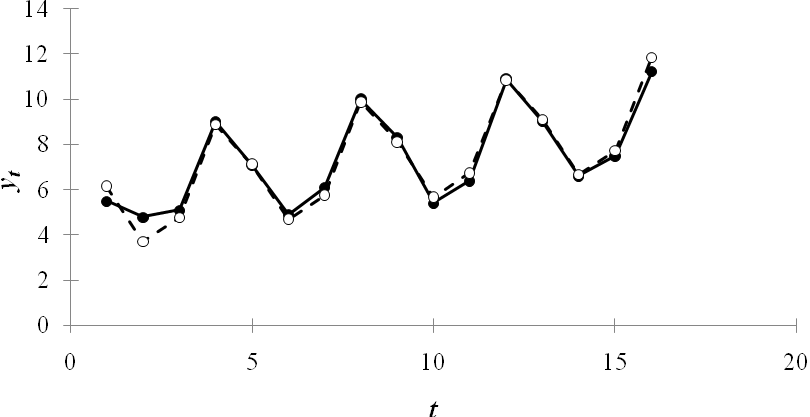 Рис. 6. Для оценки качества построенной модели применим сумму квадратов полученных абсолютных ошибок. 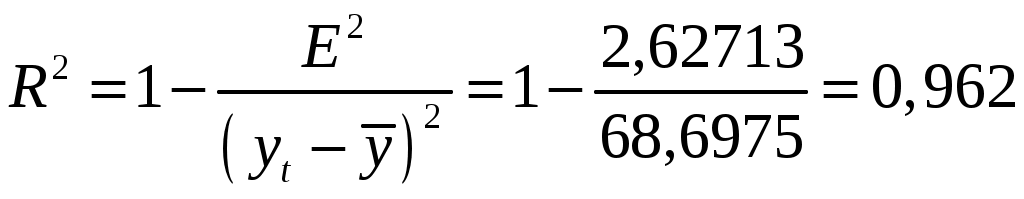 .Следовательно, можно сказать, что аддитивная модель объясняет 97% общей вариации уровней временного ряда количества правонарушений по кварталам за 4 года. Шаг 6. Прогнозирование по аддитивной модели. Предположим, что по нашему примеру необходимо дать прогноз об общем объеме потребления электроэнергии на I и II кварталы 5-го года. Прогнозное значение  уровня временного ряда в аддитивной модели есть сумма трендовой и сезонной компонент. Для определения трендовой компоненты воспользуемся уравнением тренда .Получим  ; .Значения сезонных компонент за соответствующие кварталы равны:  и  . Таким образом, ; .Т.е. в первые два квартала 5-го года следовало ожидать порядка 10,09 и 7,75 КВт потребления электроэнергии соответственно. Задача 5 Системы одновременных уравнений. Имеются структурная модель и приведенная форма модели. Используя таблицу соответствующего варианта: оценить данную структурную модель на идентификацию; исходя из приведенной формы модели уравнений найти структурные коэффициенты модели. Вариант 7. Структурная модель:  , , . Приведенная форма:  , , .Решение: Модель имеет три эндогенные (y1, y2, y3) и три экзогенные (x1, x2, x3) переменные. Проверим каждое уравнение системы на необходимые (H) и достаточное (Д) условия идентификации. Первое уравнение: Н: эндогенных переменных – 2 (y1, y2), отсутствующих экзогенных – 1 (x3). Выполняется необходимое равенство: 2=1+1, следовательно, уравнение точно идентифицируемо. Д: в первом уравнении отсутствуютy3 и x3. Построим матрицу из коэффициентов при них в других уравнениях системы:
 .Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и первое уравнение точно идентифицируемо. Второе уравнение: Н: эндогенных переменных – 3 (y1, y2,y3), отсутствующих экзогенных – 2 (x1, x3). Выполняется необходимое равенство: 3=2+1, следовательно, уравнение точно идентифицируемо. Д: во втором уравнении отсутствуют x1 и x3. Построим матрицу из коэффициентов при них в других уравнениях системы:
 .Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и второе уравнение точно идентифицируемо. Третье уравнение: Н: эндогенных переменных – 2 (y2,y3), отсутствующих экзогенных – 1 (x2). Выполняется необходимое равенство: 2=1+1, следовательно, уравнение точно идентифицируемо. Д: в третьем уравнении отсутствуют y1 и x2. Построим матрицу из коэффициентов при них в других уравнениях системы:
 .Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и третье уравнение точно идентифицируемо. Следовательно, исследуемая система точно идентифицируема и может быть решена косвенным методом наименьших квадратов. Вычислим структурные коэффициенты модели: из второго уравнения приведенной формы выразим x3 (так как его нет в первом уравнении структурной формы):  .Данное выражение содержит переменные y2, x1 и x2, которые нужны для первого уравнения структурной формы модели (СФМ). Подставим полученное выражение x3 в первое уравнение приведенной формы модели (ПФМ):   – первое уравнение СФМ;во втором уравнении СФМ нет переменных | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
