Навигация по странице:Шаг 3
|
Математика спец курс. Контрольная работа 1. Задача 1 Парная регрессия и корреляция
Шаг 2. Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними (гр. 6 табл. 14). Используем эти оценки для расчета значений сезонной компоненты 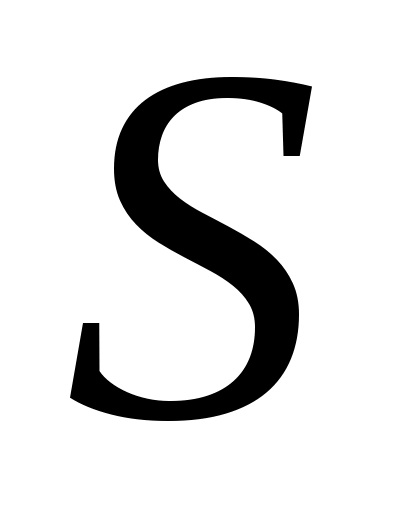 (табл. 15). Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты (табл. 15). Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты  . В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю. . В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.
Таблица 15
Показатели |
Год
|
№ квартала, 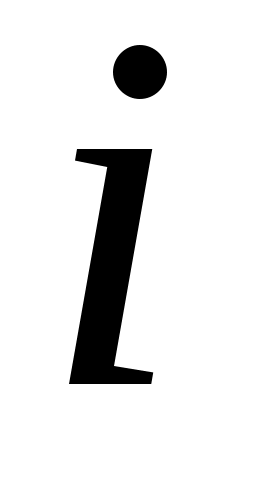
|
I
|
II
|
III
|
IV
|
|
1
|
–
|
–
|
-1,2
|
2,4875
|
2
|
0,45
|
-2
|
-1,075
|
2,6125
|
3
|
0,8125
|
-2,2375
|
-1,4375
|
2,825
|
4
|
0,6375
|
-1,9375
|
–
|
–
|
Всего за 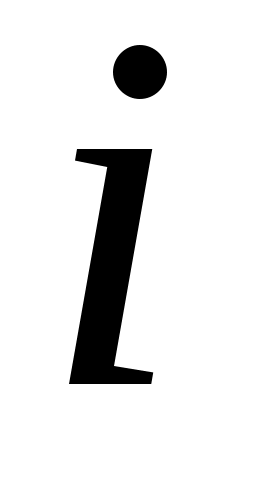 -й квартал -й квартал
|
|
1,9
|
-6,175
|
-3,7125
|
7,925
|
Средняя оценка сезонной компоненты для 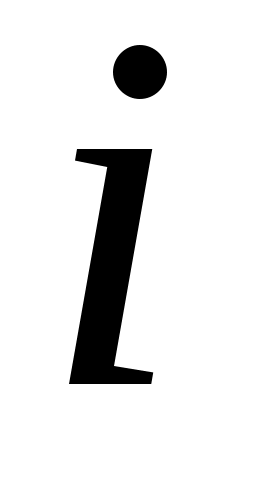 -го квартала, -го квартала, 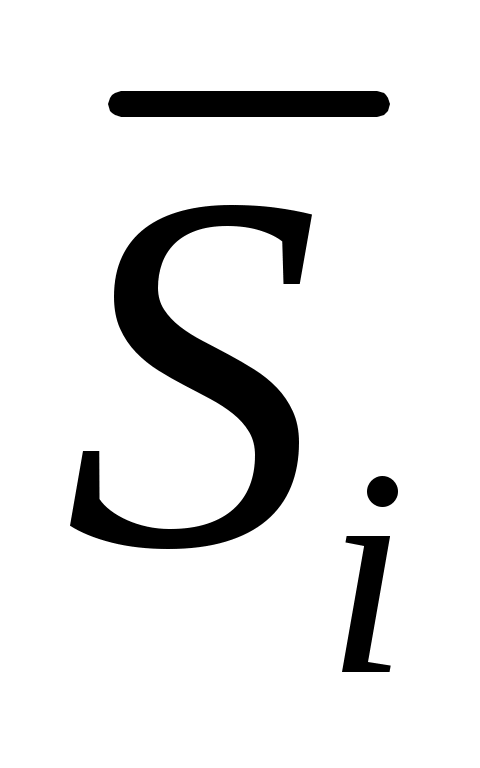
|
|
0,633
|
-2,058
|
-1,238
|
2,642
|
Скорректированная сезонная компонента, 
|
|
0,63825
|
-2,05275
|
-1,23275
|
2,64725
|
Для данной модели имеем:
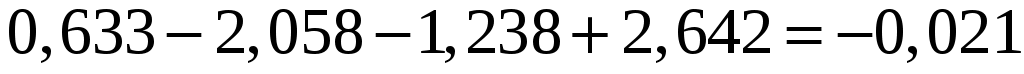 . .
Корректирующий коэффициент: 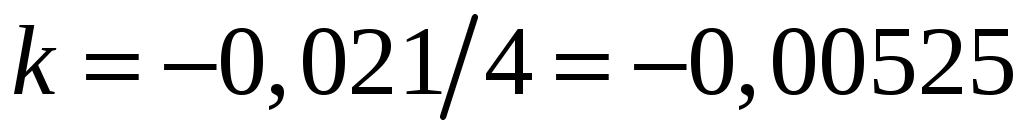 . .
Рассчитываем скорректированные значения сезонной компоненты (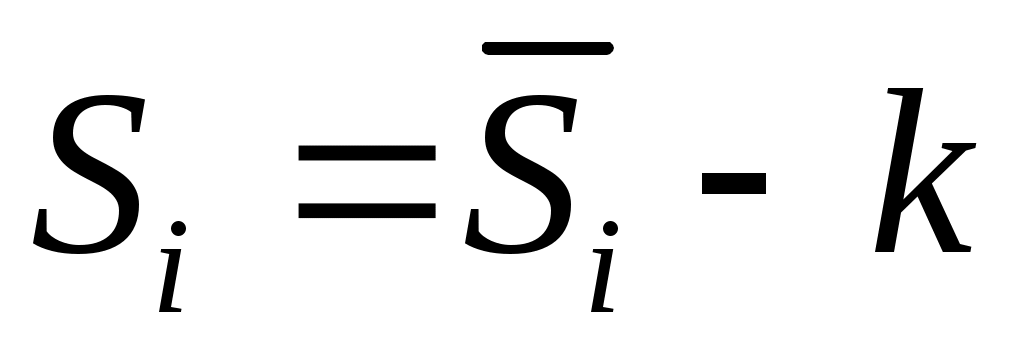 ) и заносим полученные данные в таблицу 15. ) и заносим полученные данные в таблицу 15.
Проверим равенство нулю суммы значений сезонной компоненты:
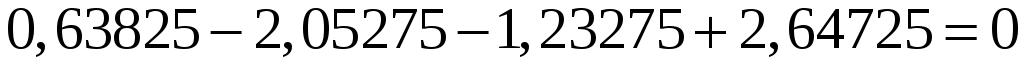 . .
Шаг 3. Исключим влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда. Получим величины 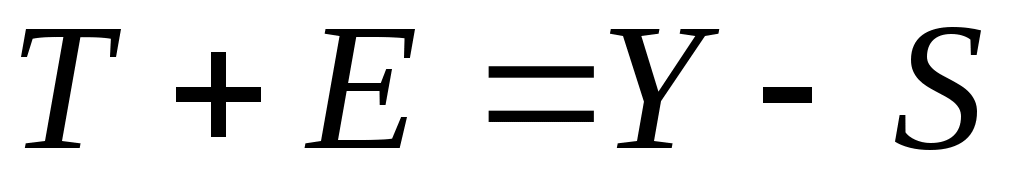 (гр. 4 табл. 16). Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту. (гр. 4 табл. 16). Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.
|
|
|
 Скачать 1.59 Mb.
Скачать 1.59 Mb.