Задача 3 Нелинейная регрессия
Динамика выпуска продукции Финляндии характеризуется данными (млн.долл.), представленными в таблице.
Требуется:
Рассчитать параметры степенной и экспоненциальной парных
регрессий.
Оценить тесноту связи с помощью показателей корреляции и
детерминации.
Рассчитать средние коэффициенты эластичности и дать сравнительную оценку силы связи фактора с результатом.
С помощью F- критерия оценить статистическую надежность результатов моделирования.
Рассчитать линейный коэффициент корреляции и детерминации, сделать вывод о целесообразности замены нелинейной зависимости линейной.
На основании пунктов 3,4,5 выбрать наилучшее уравнение регрессии.
По 27 регионам страны изучается зависимость средней заработной платы, y от валового регионального продукта (ВРП) на душу населения, x.
В представленной таблице N- это две последние цифры в номере зачетной книжки
Номер
региона
|
ВРП на душу населения,
тыс.руб., x
|
Средняя заработная плата, тыс.руб.,y
|
Номер
региона
|
ВРП на душу населения,
тыс.руб., x
|
Средняя заработная плата, тыс.руб.,y
|
1
|
35,8+N/10
|
3,5
|
15
|
32,5+N/10
|
3,3
|
2
|
22,5+N/10
|
2,6
|
16
|
32,4+N/10
|
3,3
|
3
|
28,3+N/10
|
3,2
|
17
|
50,9+N/10
|
3,9
|
4
|
26,0+N/10
|
2,6
|
18
|
44,8+N/10
|
4,7
|
5
|
20,0+N/10
|
2,6
|
19
|
79,1+N/10
|
6,5
|
6
|
31,8+N/10
|
3,5
|
20
|
47,4+N/10
|
5,0
|
7
|
30,5+N/10
|
3,1
|
21
|
53,3+N/10
|
4,5
|
8
|
29,5+N/10
|
2,9
|
22
|
33,1+N/10
|
3,7
|
9
|
41,5+N/10
|
3,4
|
23
|
48,4+N/10
|
4,5
|
10
|
41,3+N/10
|
4,8
|
24
|
61,1+N/10
|
7,2
|
11
|
34,5+N/10
|
3,0
|
25
|
38,9+N/10
|
3,4
|
12
|
34,9+N/10
|
3,1
|
26
|
26,2+N/10
|
2,9
|
13
|
34,7+N/10
|
3,3
|
27
|
59,3+N/10
|
5,4
|
14
|
26,8+N/10
|
2,6
|
|
|
|
Решение.
Регрессия в виде степенной функции имеет вид 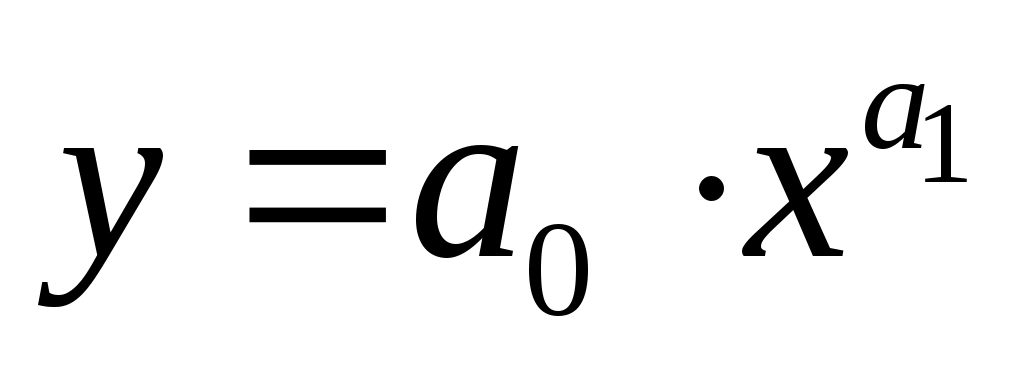 . .
Для оценки параметров линеаризуем модель путем логарифмирования:
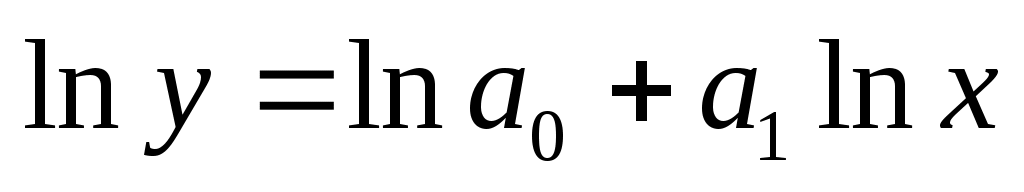 , ,
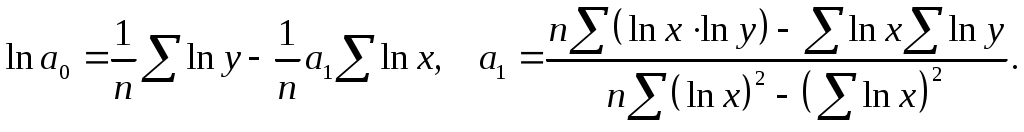
Для расчетов составим таблицу:
Таблица 3
Номер
|
x
|
y
|
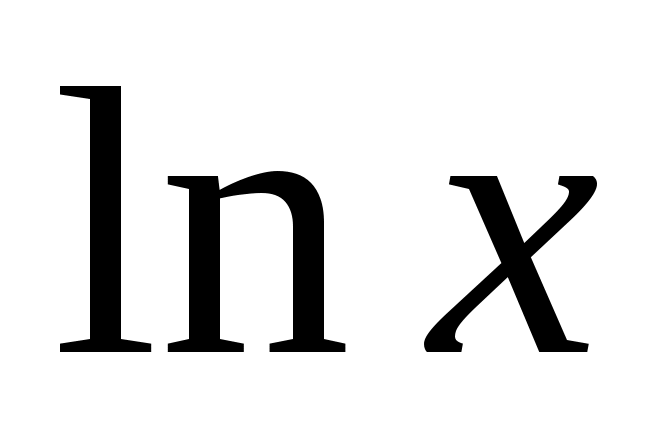
|
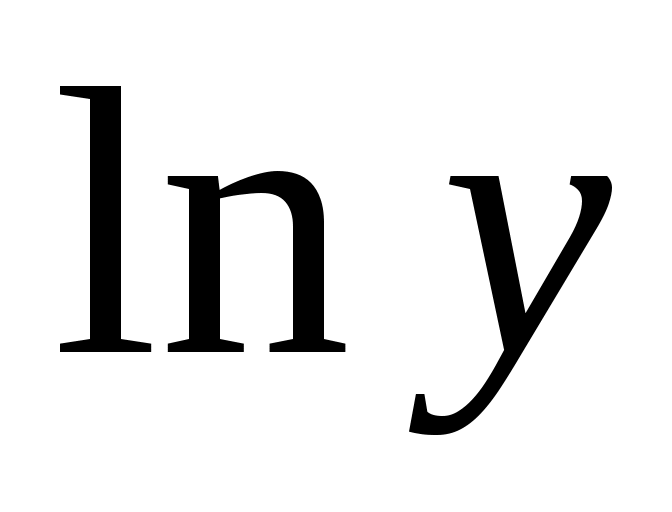
|
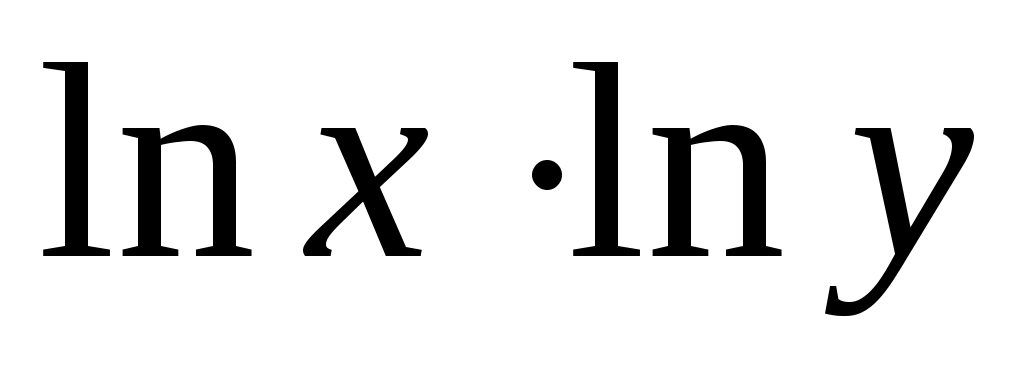
|
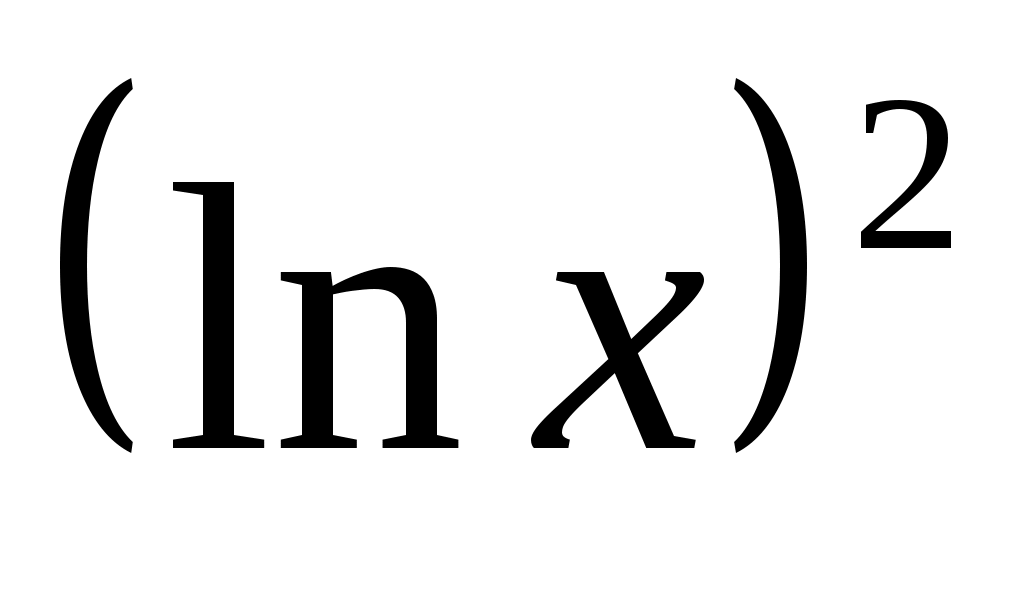
|
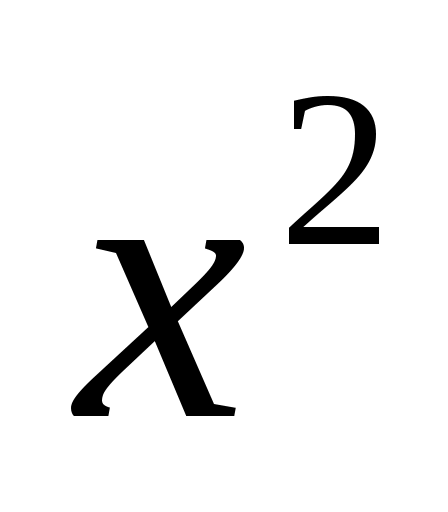
|
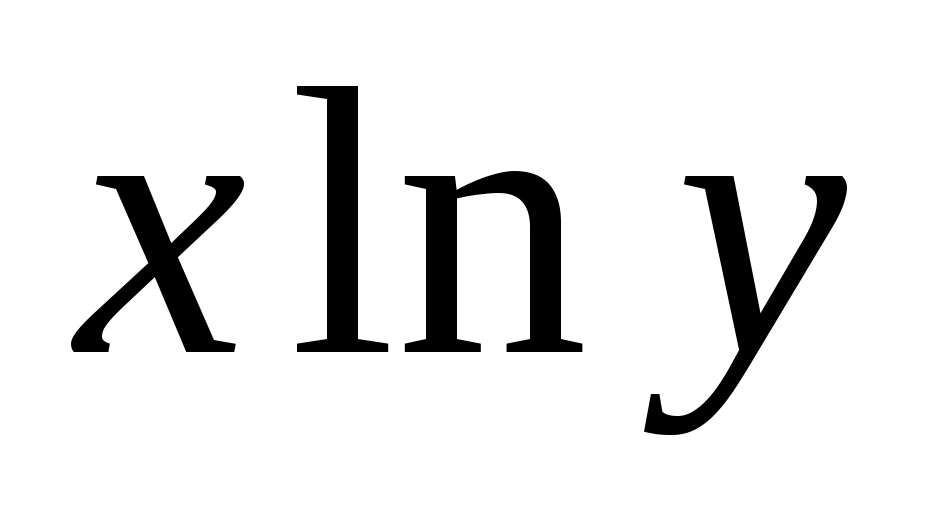
|
1
|
43,5
|
3,5
|
3,7728
|
1,2528
|
4,7266
|
14,234
|
1892,25
|
54,4968
|
2
|
30,2
|
2,6
|
3,4078
|
0,9555
|
3,2562
|
11,6131
|
912,04
|
28,8561
|
3
|
36
|
3,2
|
3,5835
|
1,1632
|
4,1683
|
12,8415
|
1296
|
41,8752
|
4
|
33,7
|
2,6
|
3,5175
|
0,9555
|
3,361
|
12,3728
|
1135,69
|
32,2004
|
5
|
27,7
|
2,6
|
3,3214
|
0,9555
|
3,1736
|
11,0317
|
767,29
|
26,4674
|
6
|
39,5
|
3,5
|
3,6763
|
1,2528
|
4,6057
|
13,5152
|
1560,25
|
49,4856
|
7
|
38,2
|
3,1
|
3,6428
|
1,1314
|
4,1215
|
13,27
|
1459,24
|
43,2195
|
8
|
37,2
|
2,9
|
3,6163
|
1,0647
|
3,8503
|
13,0776
|
1383,84
|
39,6068
|
9
|
49,2
|
3,4
|
3,8959
|
1,2238
|
4,7678
|
15,178
|
2420,64
|
60,211
|
10
|
49
|
4,8
|
3,8918
|
1,5686
|
6,1047
|
15,1461
|
2401
|
76,8614
|
|
42,2
|
3
|
3,7424
|
1,0986
|
4,1114
|
14,0056
|
1780,84
|
46,3609
|
|
42,6
|
3,1
|
3,7519
|
1,1314
|
4,2449
|
14,0768
|
1814,76
|
48,1976
|
|
42,4
|
3,3
|
3,7471
|
1,1939
|
4,4737
|
14,0408
|
1797,76
|
50,6214
|
|
34,5
|
2,6
|
3,541
|
0,9555
|
3,3834
|
12,5387
|
1190,25
|
32,9648
|
|
40,2
|
3,3
|
3,6939
|
1,1939
|
4,4101
|
13,6449
|
1616,04
|
47,9948
|
|
40,1
|
3,3
|
3,6914
|
1,1939
|
4,4072
|
13,6264
|
1608,01
|
47,8754
|
|
58,6
|
3,9
|
4,0707
|
1,361
|
5,5402
|
16,5706
|
3433,96
|
79,7546
|
|
52,5
|
4,7
|
3,9608
|
1,5476
|
6,1297
|
15,6879
|
2756,25
|
81,249
|
|
86,8
|
6,5
|
4,4636
|
1,8718
|
8,355
|
19,9237
|
7534,24
|
162,472
|
|
55,1
|
5
|
4,0091
|
1,6094
|
6,4522
|
16,0729
|
3036,01
|
88,6779
|
|
61
|
4,5
|
4,1109
|
1,5041
|
6,1832
|
16,8995
|
3721
|
91,7501
|
|
40,8
|
3,7
|
3,7087
|
1,3083
|
4,8521
|
13,7545
|
1664,64
|
53,3786
|
|
56,1
|
4,5
|
4,0271
|
1,5041
|
6,0572
|
16,2175
|
3147,21
|
84,38
|
|
68,8
|
7,2
|
4,2312
|
1,9741
|
8,3528
|
17,9031
|
4733,44
|
135,818
|
|
46,6
|
3,4
|
3,8416
|
1,2238
|
4,7014
|
14,7579
|
2171,56
|
57,0291
|
|
33,9
|
2,9
|
3,5234
|
1,0647
|
3,7514
|
12,4143
|
1149,21
|
36,0933
|
|
67
|
5,4
|
4,2047
|
1,6864
|
7,0908
|
17,6795
|
4489
|
112,989
|
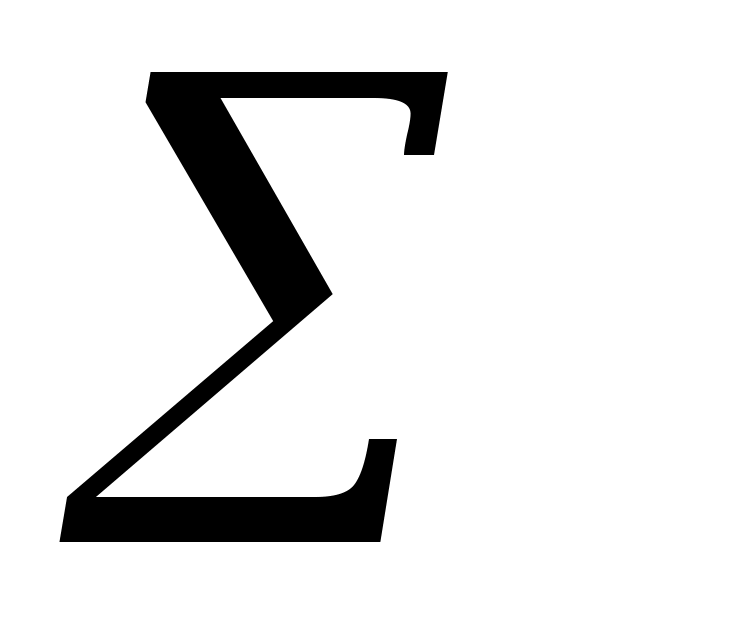
|
1253,4
|
102,5
|
102,646
|
34,9463
|
134,6324
|
392,095
|
62872,4
|
1710,89
|
Среднее
значение
|
46,4222
|
3,7963
|
3,8017
|
1,2943
|
–
|
–
|
2328,61
|
–
|
Таким образом, 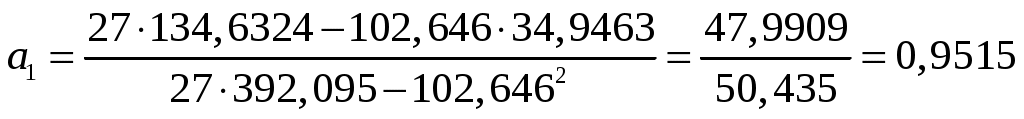 , , 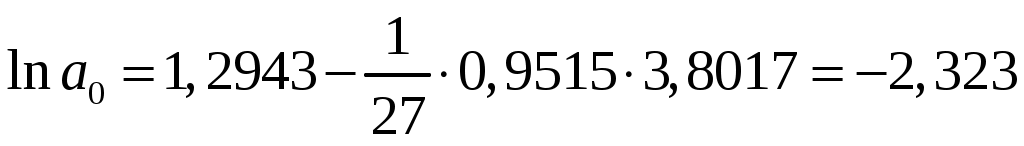 . .
Уравнение регрессии 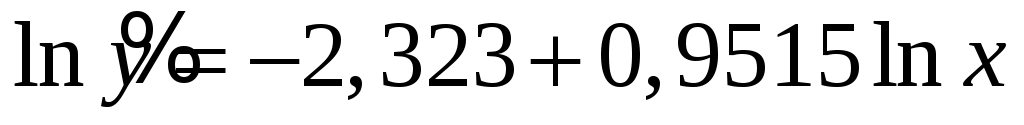 . .
Выполнив потенцирование, получим 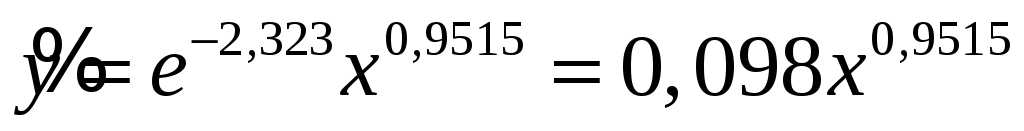 . .
Параметр 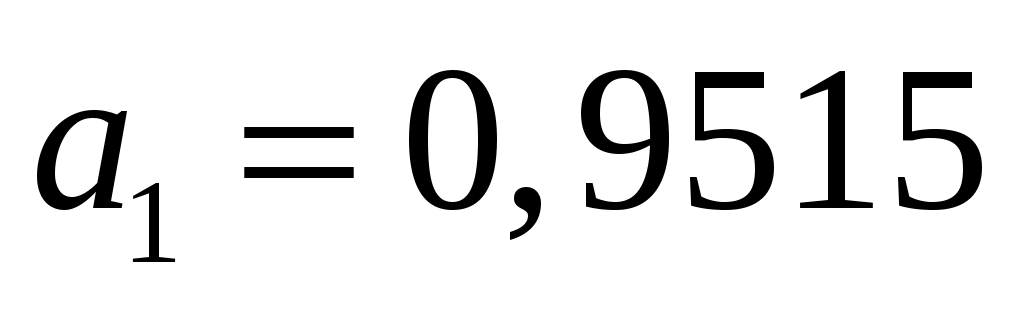 является коэффициентом эластичности и означает, что с ростом валового регионального продукта на 1% уровень заработной платы на 0,95%. является коэффициентом эластичности и означает, что с ростом валового регионального продукта на 1% уровень заработной платы на 0,95%.
Регрессия в виде экспоненциальной функции имеет вид 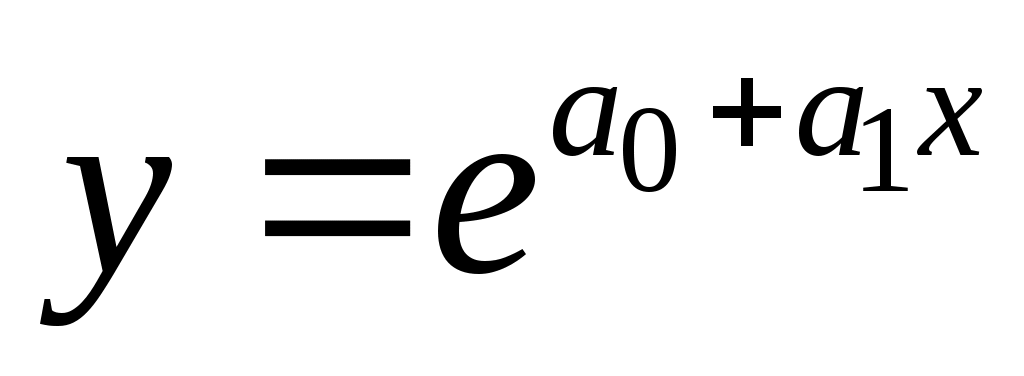 . .
Для оценки параметров линеаризуем модель путем логарифмирования:
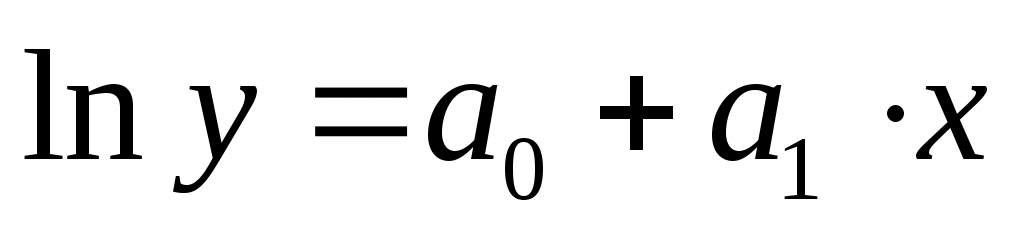 , ,
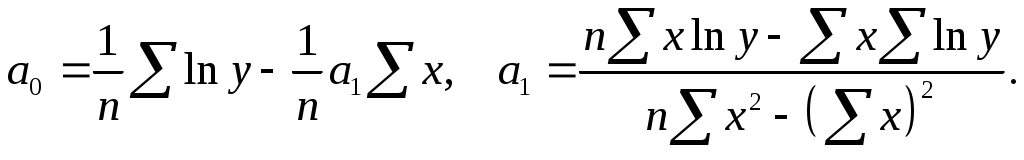
Расчетные данные приведены в таблице выше. Имеем:
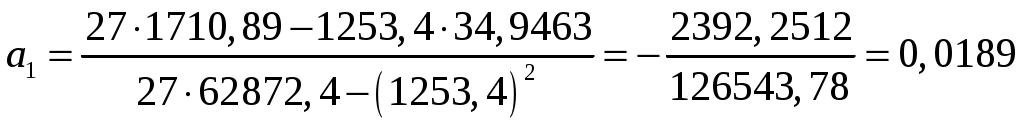 , , 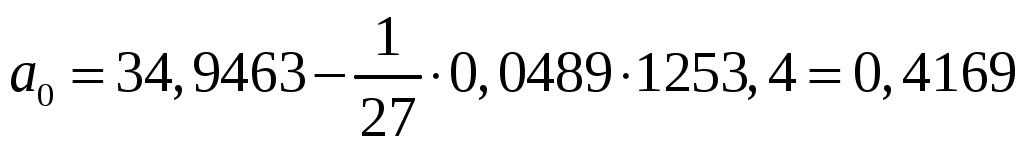 . .
Уравнение регрессии 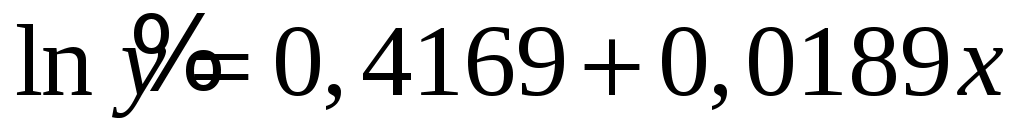 . .
Выполнив потенцирование, получим 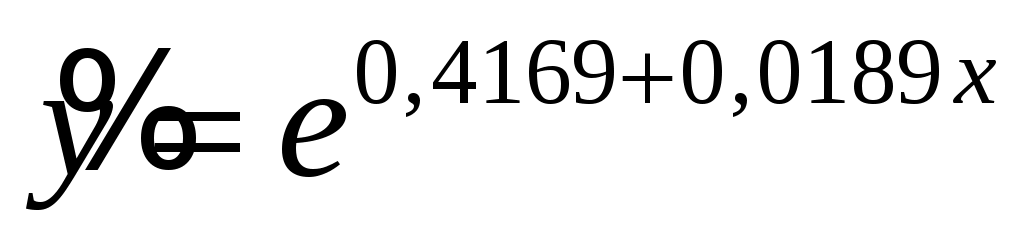
2,3. Для расчета показателей корреляции и детерминации необходимо рассчитать теоретические значения  по построенным моделям. Для этого подставим значенияx в уравнения по построенным моделям. Для этого подставим значенияx в уравнения 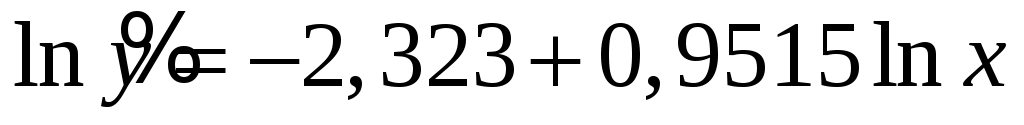 и и 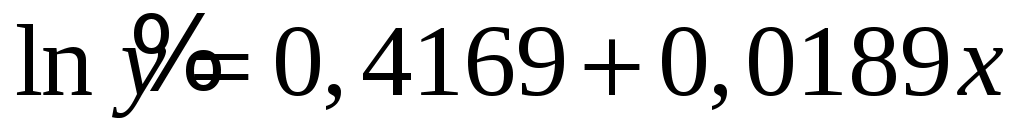 , а результаты пропотенцируем. , а результаты пропотенцируем.
Расчеты приведем в таблице. Индексы корреляции и детерминации будем рассчитывать по формулам 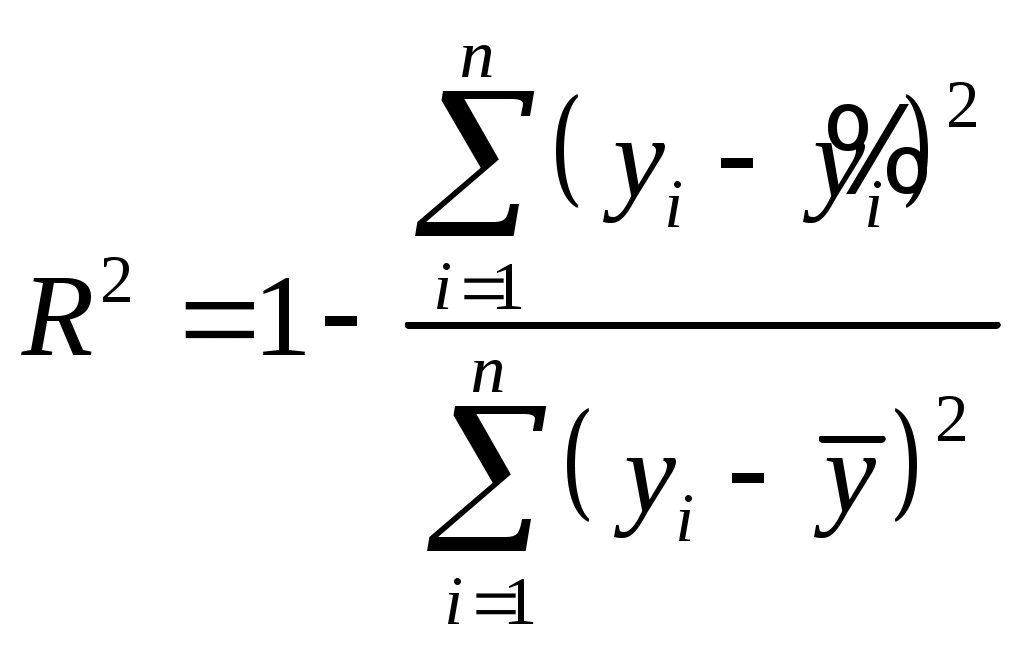 , , 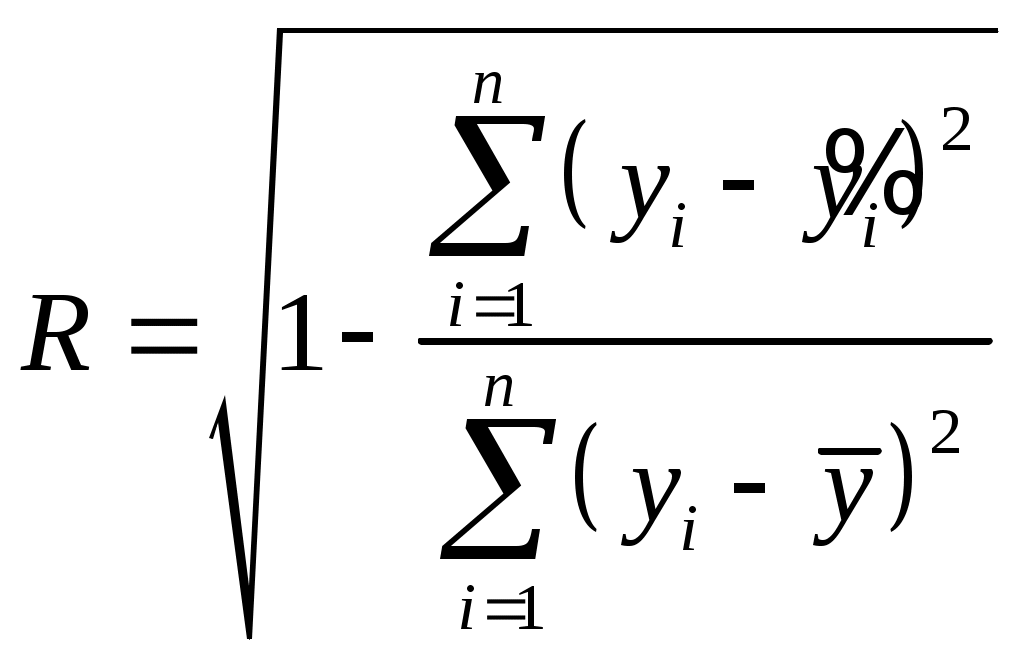 . .
Таблица 4
Номер
|
y
|
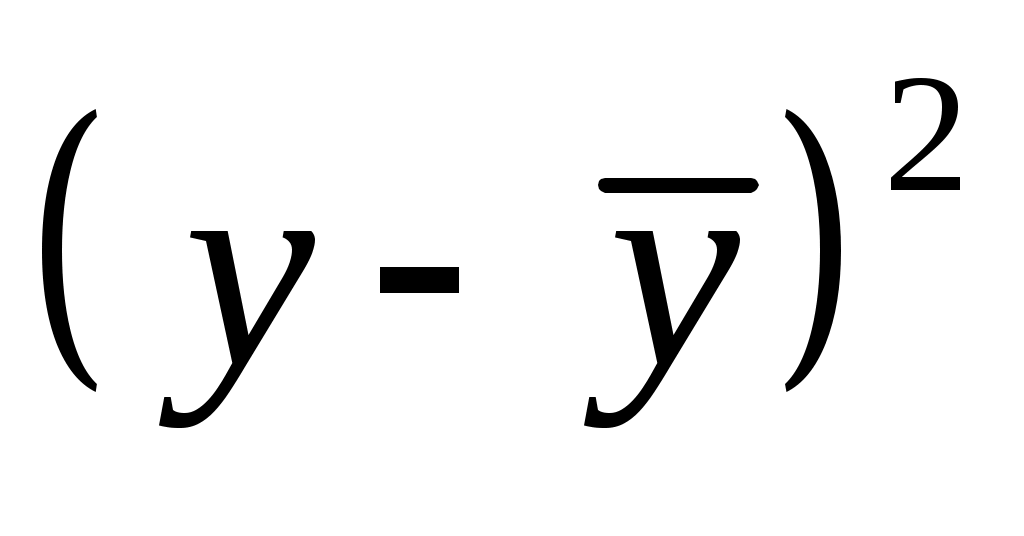
|
Степенная функция
|
Экспоненциальная функция
|
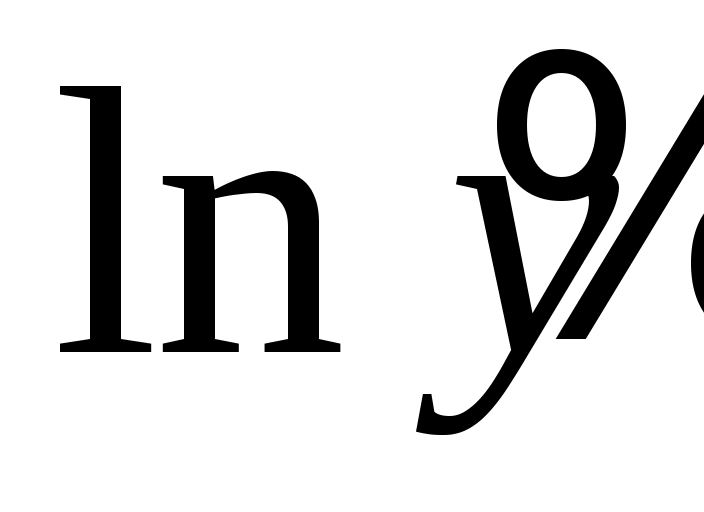
|
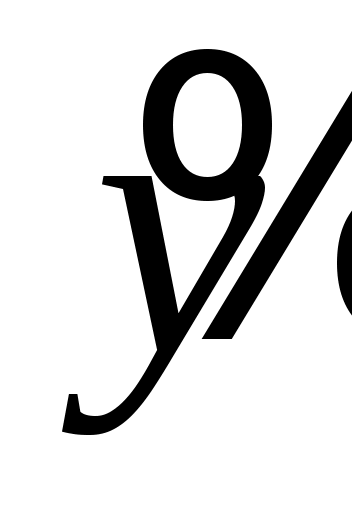
|
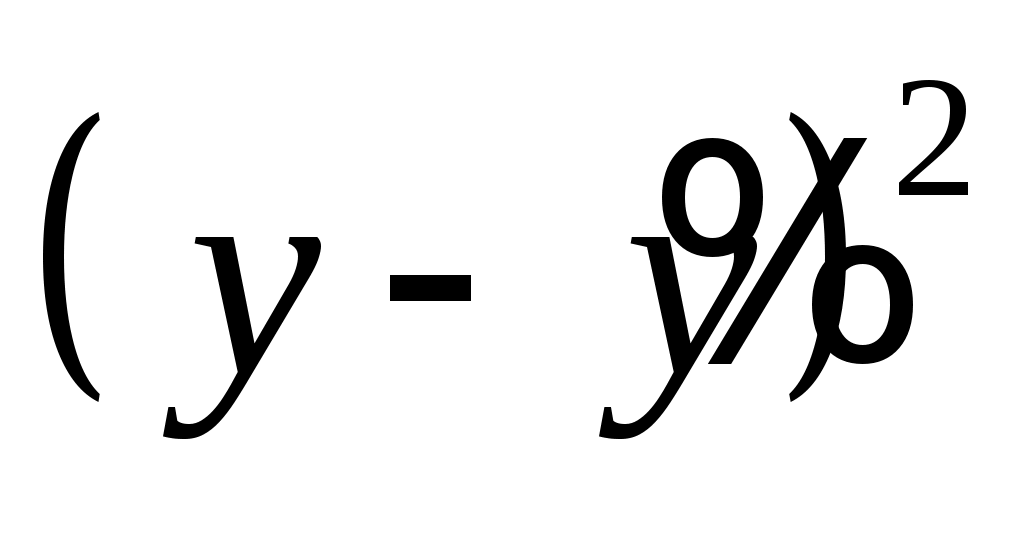
|
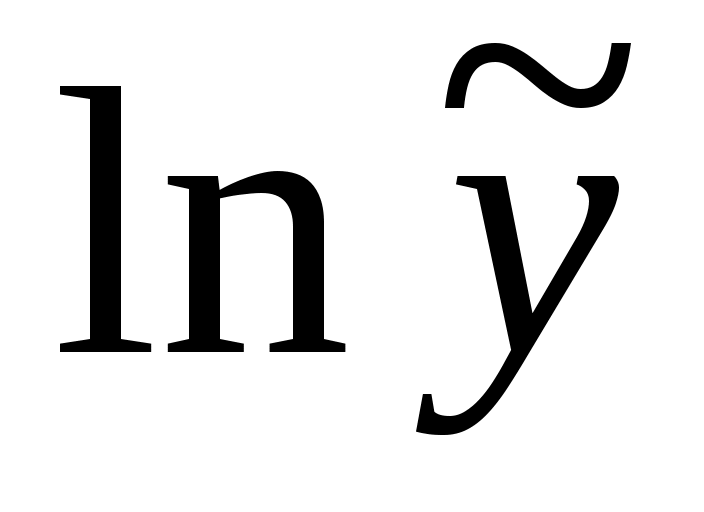
|
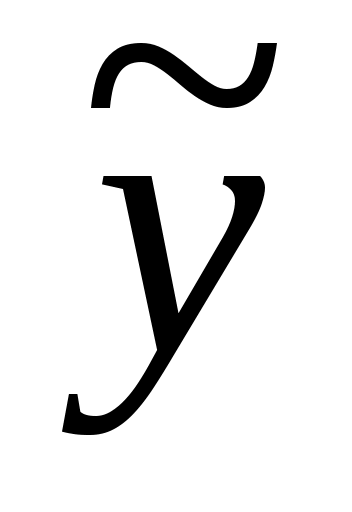
|
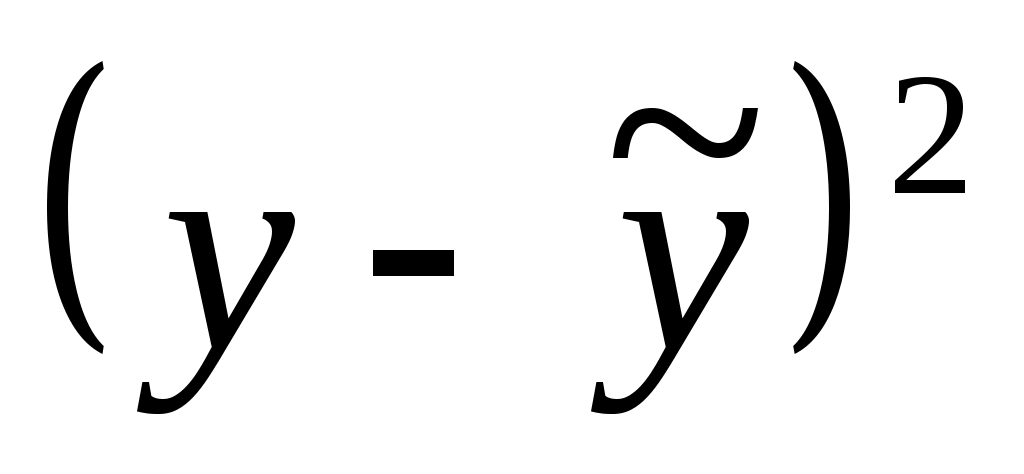
|
1
|
3,5
|
0,1
|
1,2668
|
3,5495
|
0,0025
|
1,2391
|
3,4525
|
0,0023
|
2
|
2,6
|
1,4
|
0,9195
|
2,508
|
0,0085
|
0,9877
|
2,6851
|
0,0072
|
3
|
3,2
|
0,4
|
1,0867
|
2,9645
|
0,0555
|
1,0973
|
2,9961
|
0,0416
|
4
|
2,6
|
1,4
|
1,0239
|
2,784
|
0,0339
|
1,0538
|
2,8685
|
0,0721
|
5
|
2,6
|
1,4
|
0,8373
|
2,3101
|
0,084
|
0,9404
|
2,561
|
0,0015
|
6
|
3,5
|
0,1
|
1,175
|
3,2381
|
0,0686
|
1,1635
|
3,2011
|
0,0893
|
7
|
3,1
|
0,5
|
1,1431
|
3,1365
|
0,0013
|
1,1389
|
3,1233
|
0,0005
|
8
|
2,9
|
0,8
|
1,1179
|
3,0584
|
0,0251
|
1,12
|
3,0649
|
0,0272
|
9
|
3,4
|
0,2
|
1,3839
|
3,9904
|
0,3486
|
1,3468
|
3,8451
|
0,1981
|
10
|
4,8
|
1
|
1,38
|
3,9749
|
0,6808
|
1,343
|
3,8305
|
0,9399
|
|
3
|
0,6
|
1,2379
|
3,4484
|
0,2011
|
1,2145
|
3,3686
|
0,1359
|
|
3,1
|
0,5
|
1,2469
|
3,4795
|
0,144
|
1,222
|
3,394
|
0,0864
|
|
3,3
|
0,2
|
1,2424
|
3,4639
|
0,0269
|
1,2183
|
3,3814
|
0,0066
|
|
2,6
|
1,4
|
1,0463
|
2,8471
|
0,0611
|
1,069
|
2,9125
|
0,0977
|
|
3,3
|
0,2
|
1,1917
|
3,2927
|
0,0001
|
1,1767
|
3,2437
|
0,0032
|
|
3,3
|
0,2
|
1,1894
|
3,2851
|
0,0002
|
1,1748
|
3,2375
|
0,0039
|
|
3,9
|
0
|
1,5503
|
4,7129
|
0,6608
|
1,5244
|
4,5924
|
0,4794
|
|
4,7
|
0,8
|
1,4457
|
4,2448
|
0,2072
|
1,4092
|
4,0927
|
0,3688
|
|
6,5
|
7,3
|
1,9241
|
6,849
|
0,1218
|
2,0574
|
7,8256
|
1,7572
|
|
5
|
1,4
|
1,4917
|
4,4446
|
0,3085
|
1,4583
|
4,2986
|
0,492
|
|
4,5
|
0,5
|
1,5885
|
4,8964
|
0,1571
|
1,5698
|
4,8057
|
0,0935
|
|
3,7
|
0
|
1,2058
|
3,3394
|
0,13
|
1,188
|
3,2805
|
0,176
|
|
4,5
|
0,5
|
1,5088
|
4,5213
|
0,0005
|
1,4772
|
4,3807
|
0,0142
|
|
7,2
|
11,6
|
1,703
|
5,4904
|
2,9227
|
1,7172
|
5,5689
|
2,6605
|
|
3,4
|
0,2
|
1,3323
|
3,7897
|
0,1519
|
1,2976
|
3,6605
|
0,0679
|
|
2,9
|
0,8
|
1,0295
|
2,7997
|
0,0101
|
1,0576
|
2,8795
|
0,0004
|
|
5,4
|
2,6
|
1,6778
|
5,3538
|
0,0021
|
1,6832
|
5,3828
|
0,0003
|
|
102,5
|
36,1
|
–
|
–
|
6,4149
|
–
|
–
|
7,8236
|
Для степенной функции индекс детерминации составит 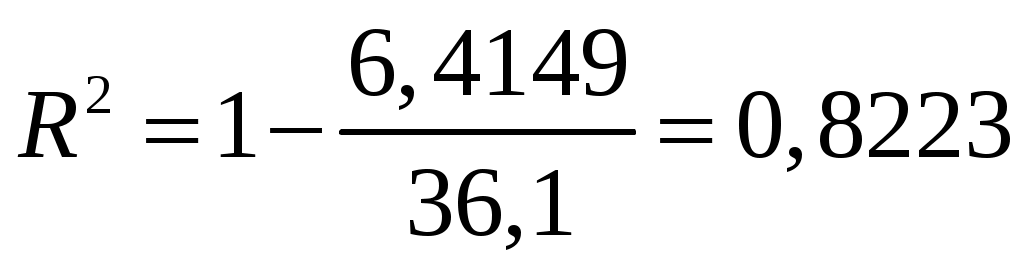 , а индекс корреляции , а индекс корреляции 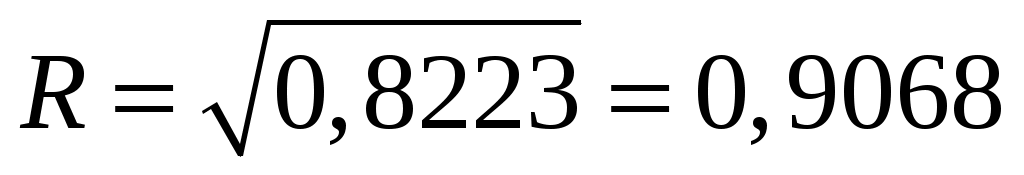 . Таким образом, связь между рассматриваемыми признаками достаточно тесная. Величина индекса детерминации говорит о том, что 91 % изменчивости уровня заработной платы объясняется данным уравнением. . Таким образом, связь между рассматриваемыми признаками достаточно тесная. Величина индекса детерминации говорит о том, что 91 % изменчивости уровня заработной платы объясняется данным уравнением.
F-критерий Фишера составит :
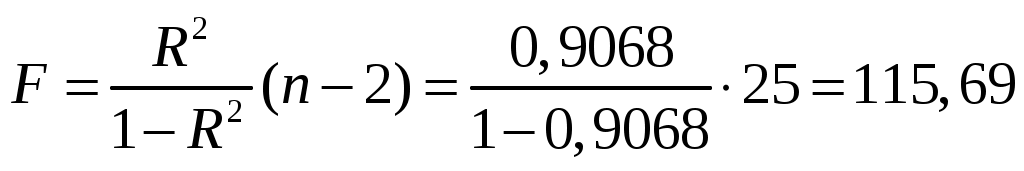 . .
Это значение превышает табличное значение на 5% уровне значимости 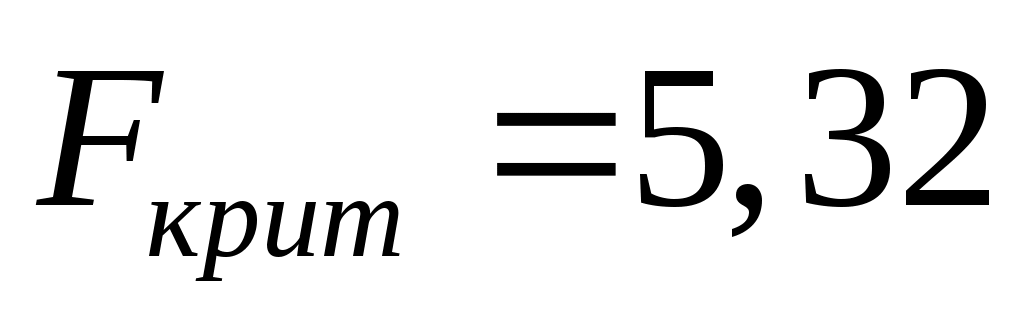 , следовательно найденное уравнение регрессии , следовательно найденное уравнение регрессии 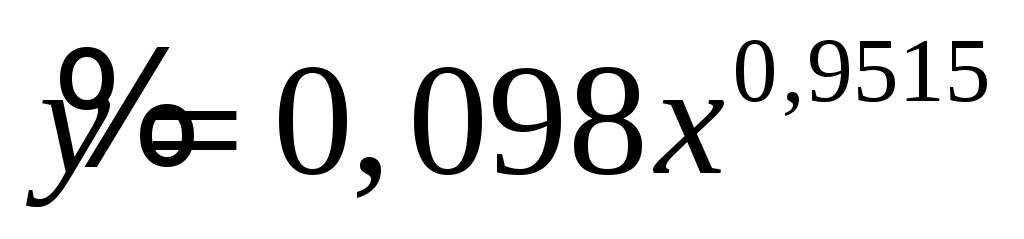 статистически значимо. статистически значимо.
Для экспоненциальной функции индекс детерминации составит 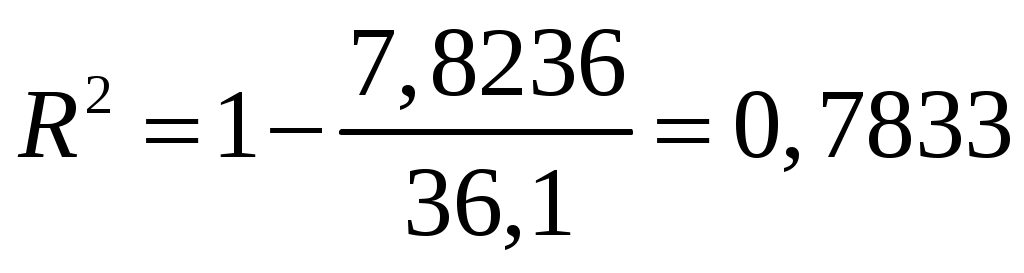 , индекс корреляции , индекс корреляции 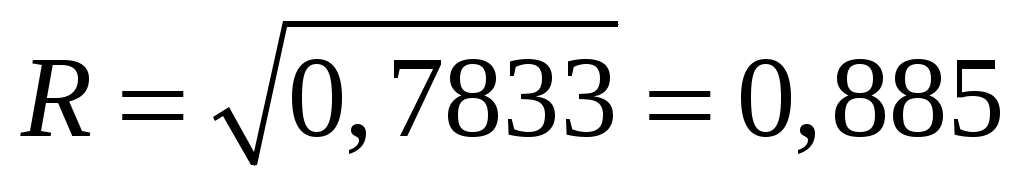 . Связь также является достаточно тесной, 88% изменчивости уровня заработной платы объясняется данным уравнением. . Связь также является достаточно тесной, 88% изменчивости уровня заработной платы объясняется данным уравнением.
F-критерий Фишера составит :
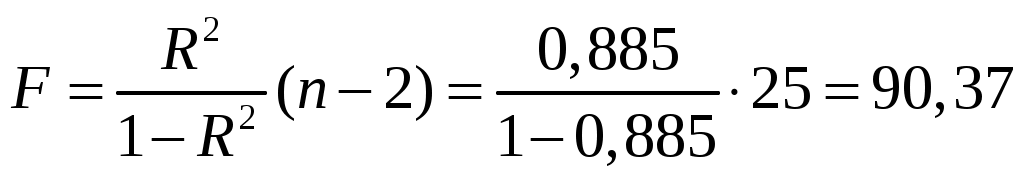 . .
Это значение превышает табличное значение на 5% уровне значимости 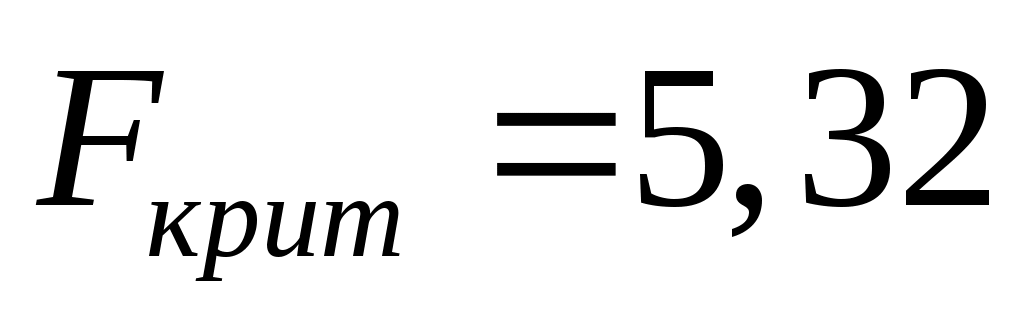 , следовательно найденное уравнение регрессии , следовательно найденное уравнение регрессии 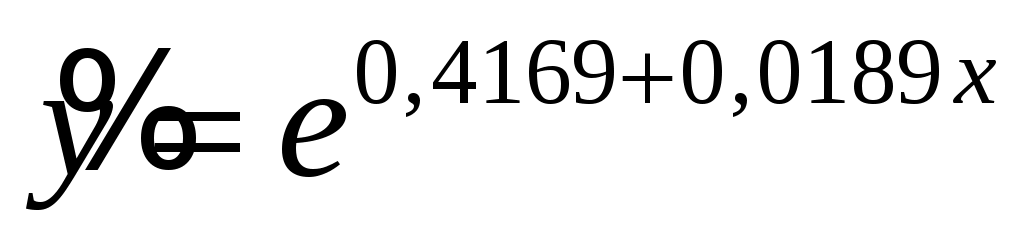 статистически значимо. статистически значимо.
4.Индексы корреляции и детерминации рассчитанных моделей различаются незначительно. Возможно, является целесообразным заменить их более простой линейной моделью. Для этого рассчитаем парные линейные коэффициенты корреляции и детерминации по формулам:
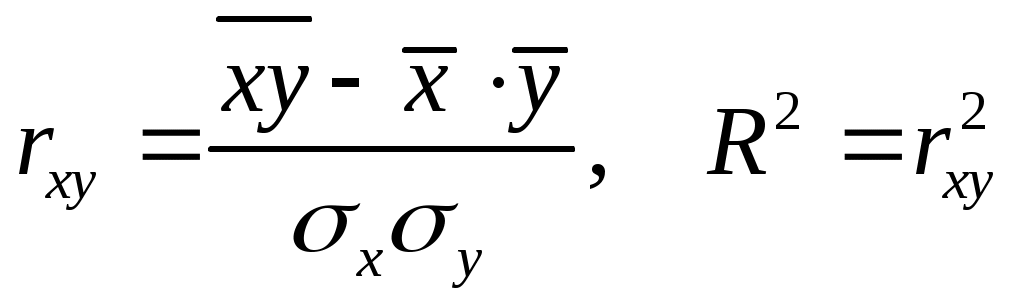 , ,
где 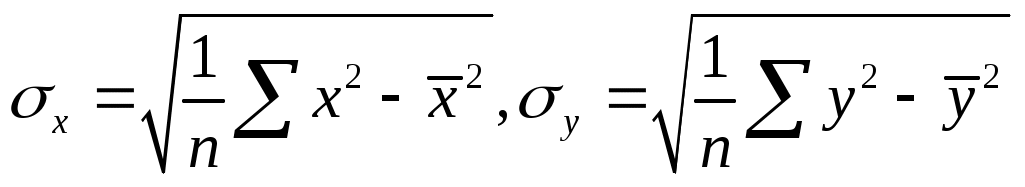 . .
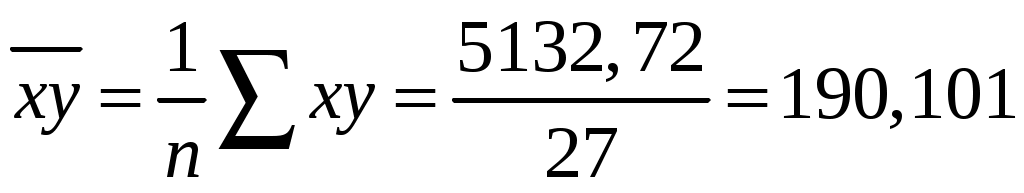 , , 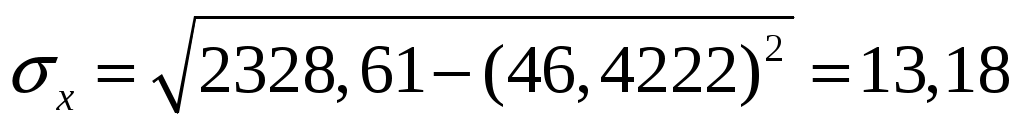 , , 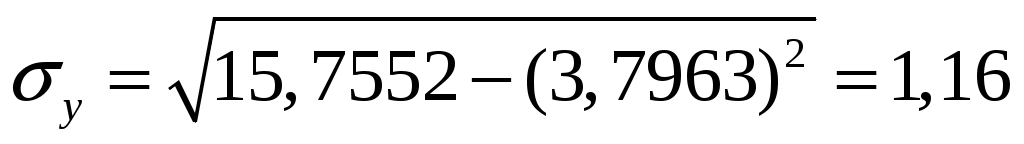 , ,
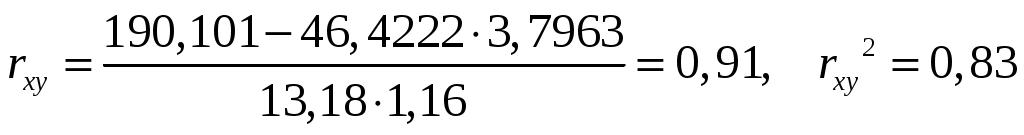 . .
В случае экспоненциальной модели разность 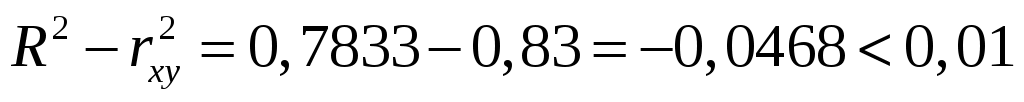 , следовательно, вместо экспоненциальной модели можно использовать линейную. , следовательно, вместо экспоненциальной модели можно использовать линейную.
В случае степенной модели 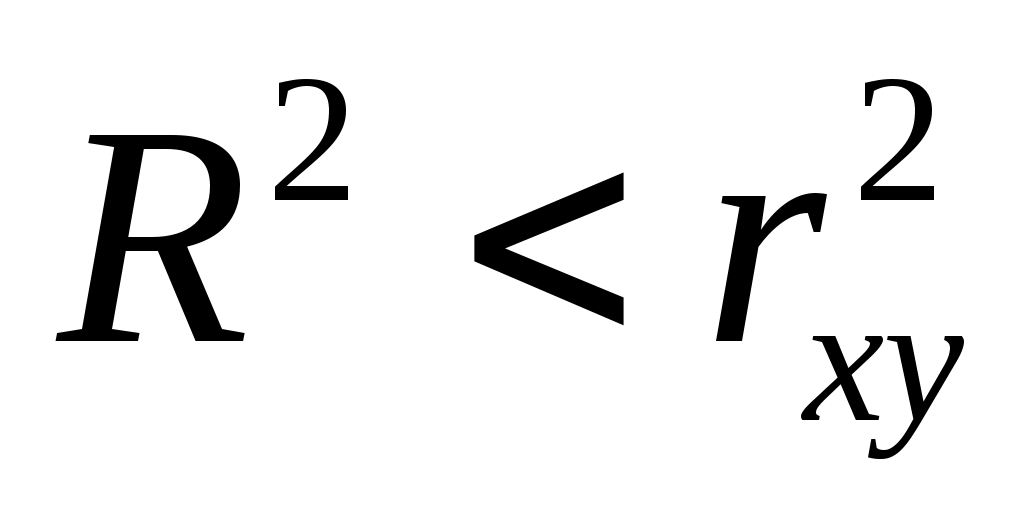 , что говорит о том, что применение более сложной формы зависимости только ухудшило качество модели. , что говорит о том, что применение более сложной формы зависимости только ухудшило качество модели.
5. Исходя из вышесказанного, делаем вывод о том, что оптимальной формой зависимости будет линейная, 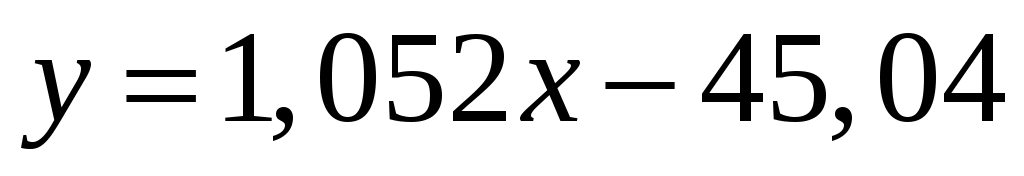 . Таким образом, при увеличении валового регионального продукта (ВРП) на душу населения на 1 тыс.руб. средняя заработная плата возрастает на 1,052 тыс.руб. . Таким образом, при увеличении валового регионального продукта (ВРП) на душу населения на 1 тыс.руб. средняя заработная плата возрастает на 1,052 тыс.руб.
Задача 4 Временные ряды
Имеются условные данные об объемах потребления электроэнергии (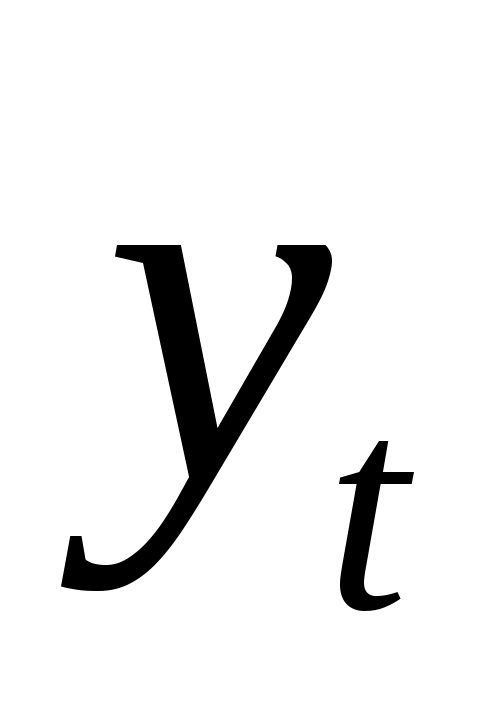 ) жителями региона за 16 кварталов. ) жителями региона за 16 кварталов.
Требуется:
Построить автокорреляционную функцию и сделать вывод о наличии сезонных колебаний.
Построить аддитивную модель временного ряда (для нечетных вариантов) или мультипликативную модель временного ряда (для четных вариантов).
Сделать прогноз на 2 квартала вперед.
Варианты 7, 8
|
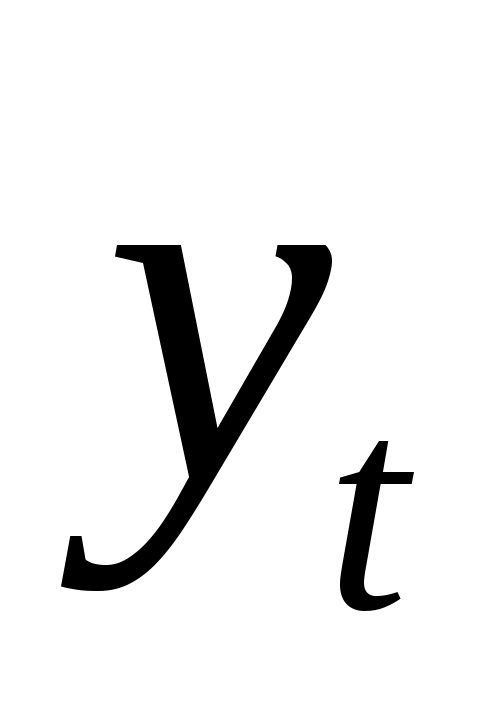
|
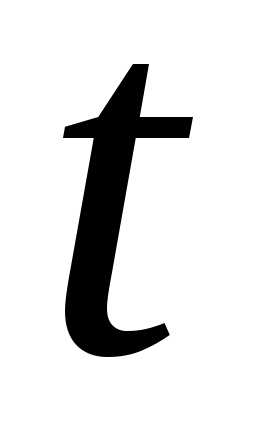
|
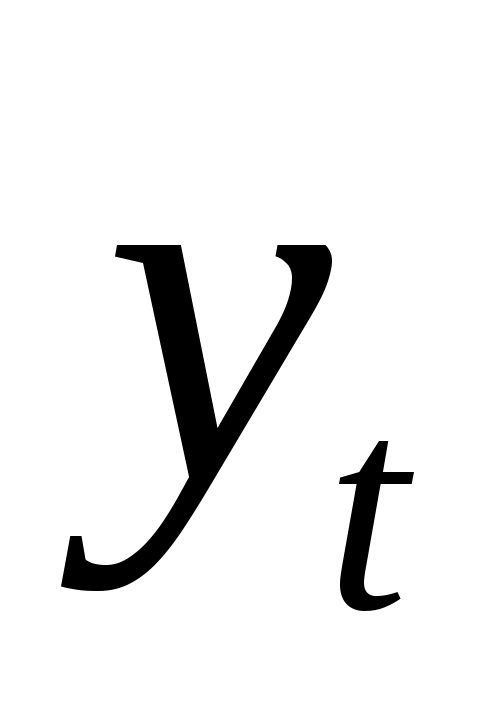
|
1
|
5,5
|
9
|
8,3
|
2
|
4,8
|
10
|
5,4
|
3
|
5,1
|
11
|
6,4
|
4
|
9,0
|
12
|
10,9
|
5
|
7,1
|
13
|
9,0
|
6
|
4,9
|
14
|
6,6
|
7
|
6,1
|
15
|
7,5
|
8
|
10,0
|
16
|
11,2
|
Решение.
1. Построим поле корреляции
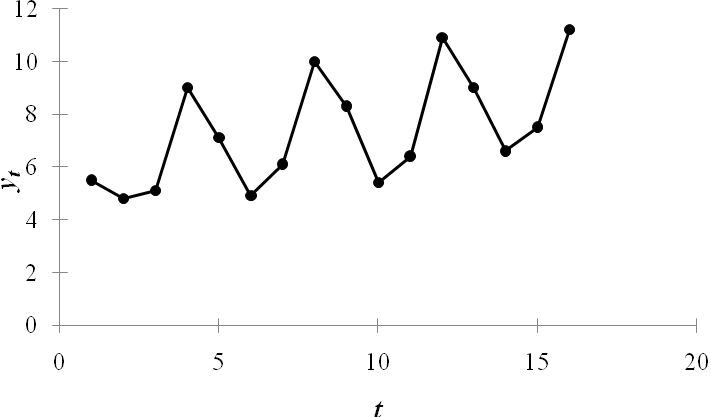
Рис. 4. Поле корреляции
Уже исходя из графика видно, что значения 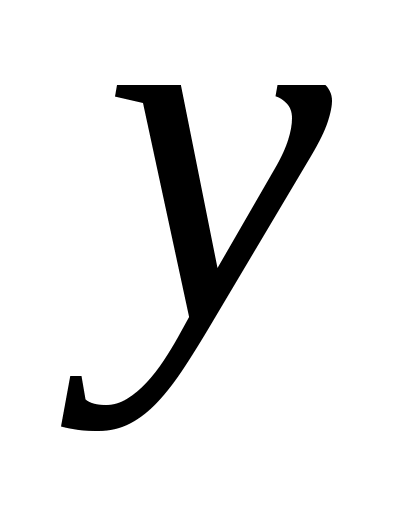 образуют пилообразную фигуру. Рассчитаем несколько последовательных коэффициентов автокорреляции. Для этого составляем первую вспомогательную таблицу. образуют пилообразную фигуру. Рассчитаем несколько последовательных коэффициентов автокорреляции. Для этого составляем первую вспомогательную таблицу.
|
 Скачать 1.59 Mb.
Скачать 1.59 Mb.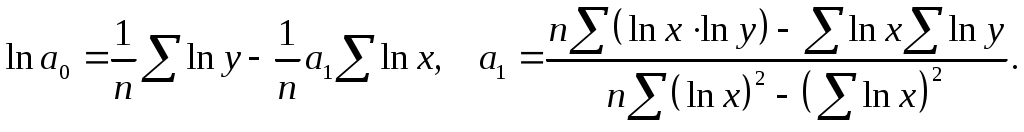
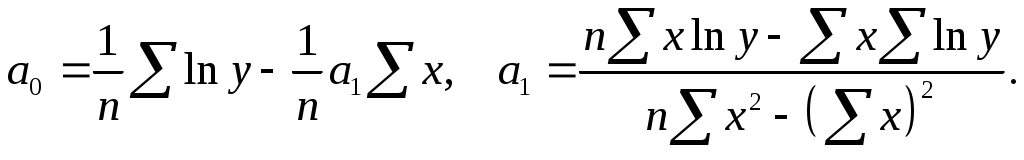
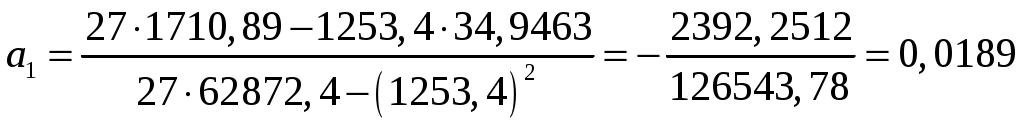 ,
, 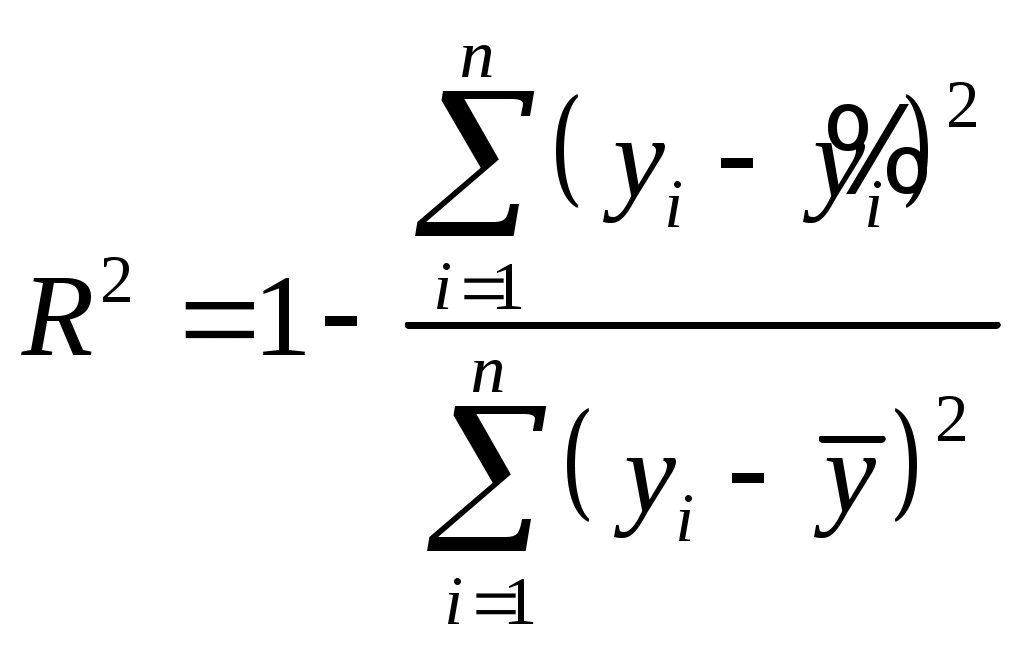 ,
, 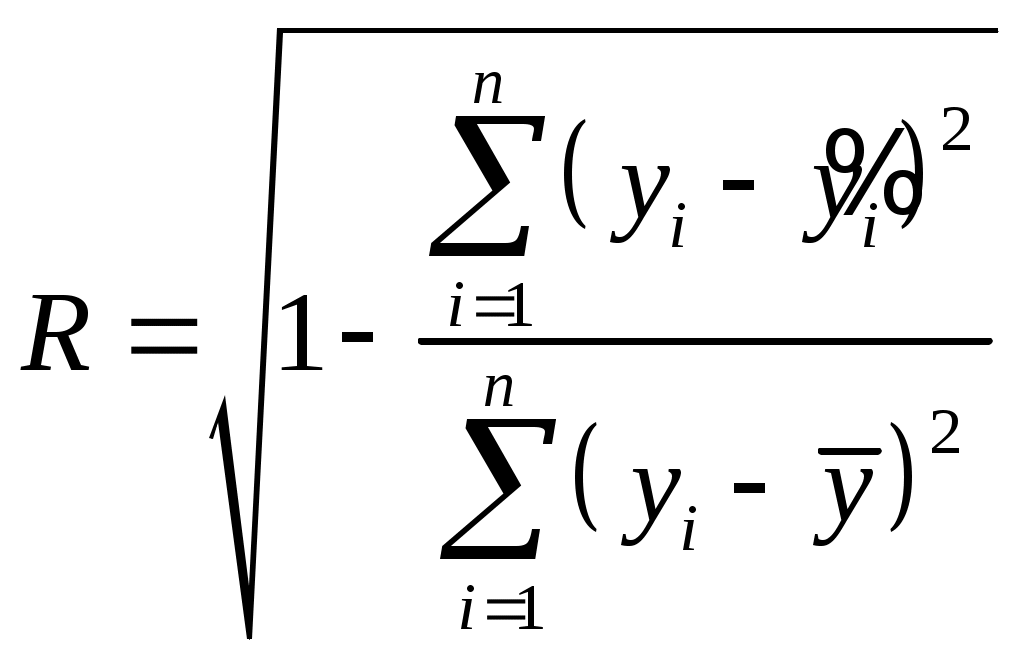 .
.
