Задача 1 Разложение чисел на простые сомножители и вычисление функции Эйлера
 Скачать 249.23 Kb. Скачать 249.23 Kb.
|
|
Задача №1 Разложение чисел на простые сомножители и вычисление функции Эйлера Для того чтобы разложить число на простые множители нужно, для начала, поделить его на 2. Если число разделится на 2 без остатка, то 2 – это первый множитель. Далее полученный результат опять делим на 2, если число разделится на 2 без остатка, то второй множитель тоже 2. Если же при делении получается остаток, то пробуем делим на 3, 4, ... n, до тех пор число не разделится без остатка. Далее рассмотрим пример из которого станет всё понятно. Задание: n=941110; 203; 8372 а) n=p, где p-простое число б) n=pq, где p,q – простые числа в) n= 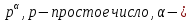 натуральное число. натуральное число.Решение Разложим число n=941110 на простые множители 941110 ÷ 2 = 470555 (первый множитель 2) 470555 ÷ 2 = 235277,5 (тут появился остаток, значит делим на 3) 470555 ÷ 3 = 156851,66 470555 ÷ 4 = 117638,75 470555 ÷ 5 = 94111 (второй множитель 5) 94111 ÷ 5 = 18822,2 94111 ÷ 6 = 15685,17 94111 ÷ 7 = 13444,43 94111 ÷ 8 = 11763,875 94111 ÷ 9 = 10456,78 94111 ÷ 10 = 9411,1 94111 ÷ 11 = 8555,54 и т.д. 94111 ÷ 94111 = 1 Получаем простые множители числа 941110: 2⋅5⋅94111 Если число делится без остатка только на 1 и на само себя, то оно является простым числом. Такое число нельзя разложить на простые множители. Функция Эйлера φ(n) — функция, равная количеству чисел ряда 0 ….. n-1, взаимно простых с n. Заметим, что из определения φ(1)=1. Пояснение: взаимно простыми называются числа, которые не имеют общих делителей, отличных от 1. Так как делителями нуля являются все натуральные числа, то 0 взаимно прост только с 1. Вычисление функции Эйлера Представим числоa в виде 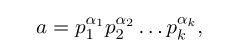 где р1……рk– простые и попарно различные. Тогда: 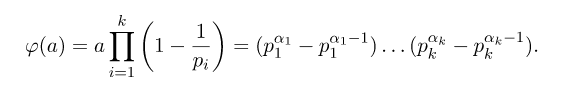 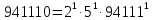 Тогда 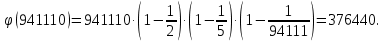 Разложим число n=203 на простые множители 203 ÷ 2 = 101,5 203 ÷ 3 = 67,7 203 ÷ 4 = 50,75 203 ÷ 5 = 40,6 203 ÷ 6 = 33,8 203 ÷ 7 = 29 (первый множитель 7) 29 ÷ 29 = 1 (второй множитель 29) Получаем простые множители числа 203: 7⋅29 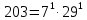 Тогда 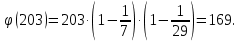 Разложим число n=8372 на простые множители 8372 ÷ 2 = 4186 (первый множитель 2) 4186 ÷ 2 = 2093 (второй множитель 2) 2093 ÷ 2 = 1046,5 2093 ÷ 3 = 697,7 2093 ÷ 4 = 523,25 2093 ÷ 5 = 418,6 2093 ÷ 6 = 348,8 2093 ÷ 7 = 299 (третий множитель 7) 299 ÷ 7 = 42,71 299 ÷ 13 = 23 (четвертый множитель 13) Получаем простые множители числа 8372: 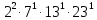 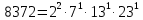 Тогда 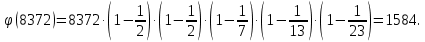 а) n=3 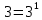 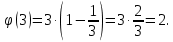 б) n=2  3=6 3=6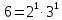 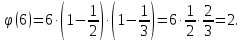 в) n= 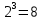 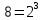 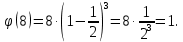 Задача №2 Нахождение числа n в произведение простых чисел Зная значение функции φ(n) = 864 найти разложение числа n = 1977 в произведение простых чисел, если известно, что n имеет 2 простых делителя. Решение Пусть 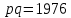 , где p и q простые. Тогда , где p и q простые. Тогда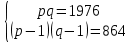 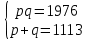 Числа p и q это решение уравнения 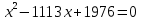 Находим 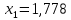 и и 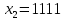 Решений нет Задача №3 Вычисление инверсий Инверсия по модулю m Во многих задачах криптографии для заданных чисел с, m требуется находить такое число d < m, что cd mod m = 1 Такое d существует тогда и только тогда, когда числа с и m взаимно простые. Число d, удовлетворяющее равенству cd mod m = 1, называется инверсией с по модулю m и часто обозначается с-1 mod m. Данное обозначение для инверсии связано с тем, что равенство cd mod m = 1 можно переписать в виде cс-1 mod m = 1. Таким образом, умножение на с-1 соответствует делению на с при вычислениях по модулю m. Инверсию по модулю m также можно вычислять с помощью обобщенного алгоритма Евклида. Покажем, как это делается. Равенство, приведенное ниже означает, что для некоторого целого k имеет место равенство cd – km = 1. Учитывая, что с и d взаимно просты, можно преобразовать это равенство следующим образом: m(-k) + cd = НОД(m,c). Значит, мы можем вычислить с-1 mod m (или найти число d ) с помощью обобщенного алгоритма Евклида. При этом значение переменной k нас не интересует. Если число d получается отрицательным, то нужно прибавить к нему m, так как по определению число a mod m берется из множества {0,1,..., m - 1}. P=3. Требуется вычислить инверсию числа 19 по модулю 3. Следовательно, вычислить 19-1mod3. Решение: 1. Число 3- простое, следовательно, число Эйлера вычисляем по формуле φ(P)=P-1. Получаем φ(P) =φ(3)=3-1 = 2. 2. Далее, по формуле (1): 19-1 (mod 3) =19 2-1 (mod 3)= 19 1 mod 3=19mod3=1. Проверка 1- инверсия числа 19 по модулю 3, так как (19*1)mod3=1 Задача №4 Модулярный шифр Модулярным называется любой простой подстановочный шифр с ключом 𝑓 : Z𝑛 → Z𝑛, который определяется формулой 𝑓(𝑥) = 𝑟𝑥 + 𝑘 (mod 𝑛) для всех 𝑥 ∈ Z𝑛. Параметры r, k фиксированы , при этом НОД(r, k)=1. Зашифруйте слово ВАЛЕРИЙ_БЫКОВ с помощью модулярного шифра с ключом 𝑓 : Z26 → Z26; 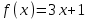 ВАЛЕРИЙ_БЫКОВ 4 2 14 7 19 11 12 1 2 29 13 17 4 Вычисляем 34 + 1 = 13 (mod 34) 32 + 1 = 7 (mod 34) 314 + 1 = 9 (mod 34) 37 + 1 = 22 (mod 34) 319 + 1 = 22 (mod 34) 311 + 1 = 1 (mod 34) 312 + 1 = 2 (mod 34) 31 + 1 = 4 (mod 34) 32 + 1 = 7 (mod 34) 329 + 1 = 20 (mod 34) 313 + 1 = 6 (mod 34) 317 + 1 = 18 (mod 34) 34 + 1 = 13 (mod 34) Зашифрованное сообщение 13 7 9 22 22 1 2 4 7 20 6 18 13 МЖИХХ_АДЖУЁСМ Задача №5 Шифр Виженера Шифр ВиженераОписание
Описание Квадрат Виженера, или таблица Виженера, также известная как tabula recta, может быть использована для шифрования и расшифрования. В шифре Цезаря каждая буква алфавита сдвигается на несколько строк; например в шифре Цезаря при сдвиге +3, A стало бы D, B стало бы E и так далее. Шифр Виженера состоит из последовательности нескольких шифров Цезаря с различными значениями сдвига. Для зашифровывания может использоваться таблица алфавитов, называемая tabula recta или квадрат (таблица) Виженера. Применительно к латинскому алфавиту таблица Виженера составляется из строк по 26 символов, причём каждая следующая строка сдвигается на несколько позиций. Таким образом, в таблице получается 26 различных шифров Цезаря. На каждом этапе шифрования используются различные алфавиты, выбираемые в зависимости от символа ключевого слова. Например, предположим, что исходный текст имеет вид: ATTACKATDAWN Человек, посылающий сообщение, записывает ключевое слово («LEMON») циклически до тех пор, пока его длина не будет соответствовать длине исходного текста: LEMONLEMONLE Первый символ исходного текста A зашифрован последовательностью L, которая является первым символом ключа. Первый символ L шифрованного текста находится на пересечении строки L и столбца A в таблице Виженера. Точно так же для второго символа исходного текста используется второй символ ключа; то есть второй символ шифрованного текста X получается на пересечении строки E и столбца T. Остальная часть исходного текста шифруется подобным способом. Исходный текст: ATTACKATDAWN Ключ: LEMONLEMONLE Зашифрованный текст: LXFOPVEFRNHR Расшифровывание производится следующим образом: находим в таблице Виженера строку, соответствующую первому символу ключевого слова; в данной строке находим первый символ зашифрованного текста. Столбец, в котором находится данный символ, соответствует первому символу исходного текста. Следующие символы зашифрованного текста расшифровываются подобным образом. Если буквы A-Z соответствуют числам 0-25, то шифрование Виженера можно записать в виде формулы: 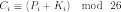 Расшифровка:  Задание: Зашифруйте ВАЛЕРИЙ_БЫКОВ с помощью шифра Виженера с ключевым словом Информационная_безопасность. Используемый алфавит – кириллица (строчные буквы) и символ ”_”, который нужно поставить в начало алфавита (его порядковый номер=1). Таким образом, мощность алфавита составляет 34 символа. Шаг равен 5 для четных вариантов, 7 – для нечетных. Исходный текст: валерий_быков Ключ: информационна Зашифрованный текст: кояу_хйхйичыв  |
