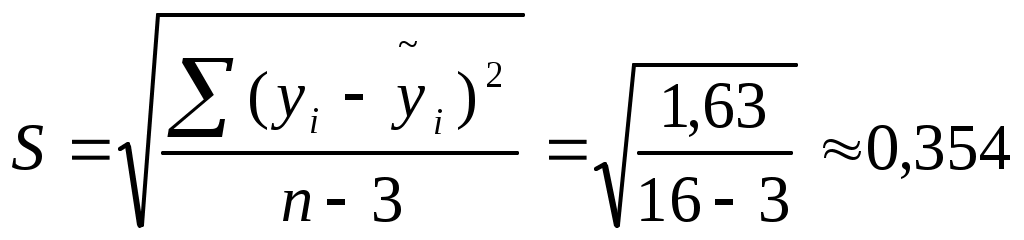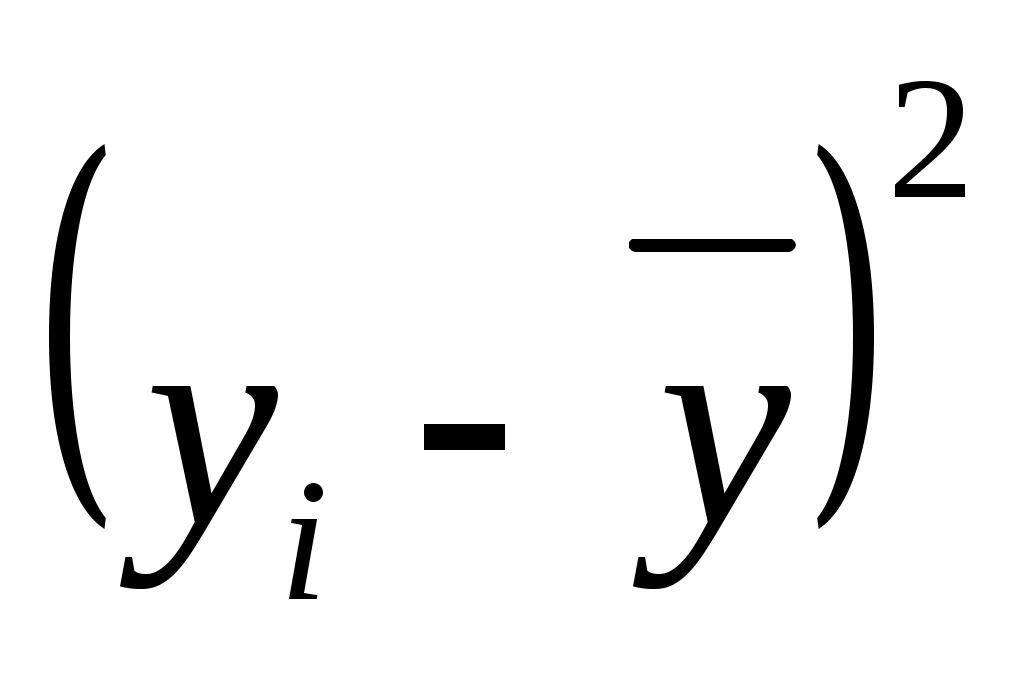|
|
эконометрика. Вариант1. Задача 1 в базе данных магазина, торгующего подержанными автомобилями, содержится информация об их потребительский свойствах и ценах
2. Множественная зависимость.
2.1. По методу наименьших квадратов найти оценки коэффициентов множественной линейной регрессионной модели 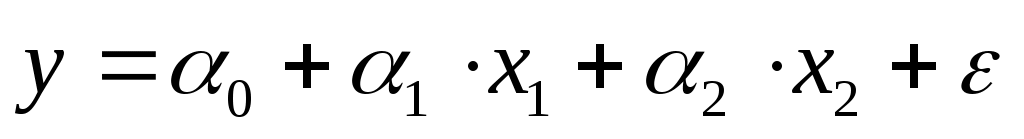
Составим матрицы 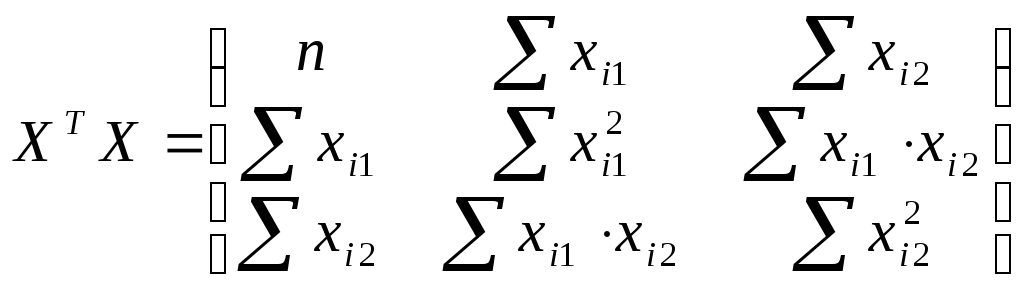 и и 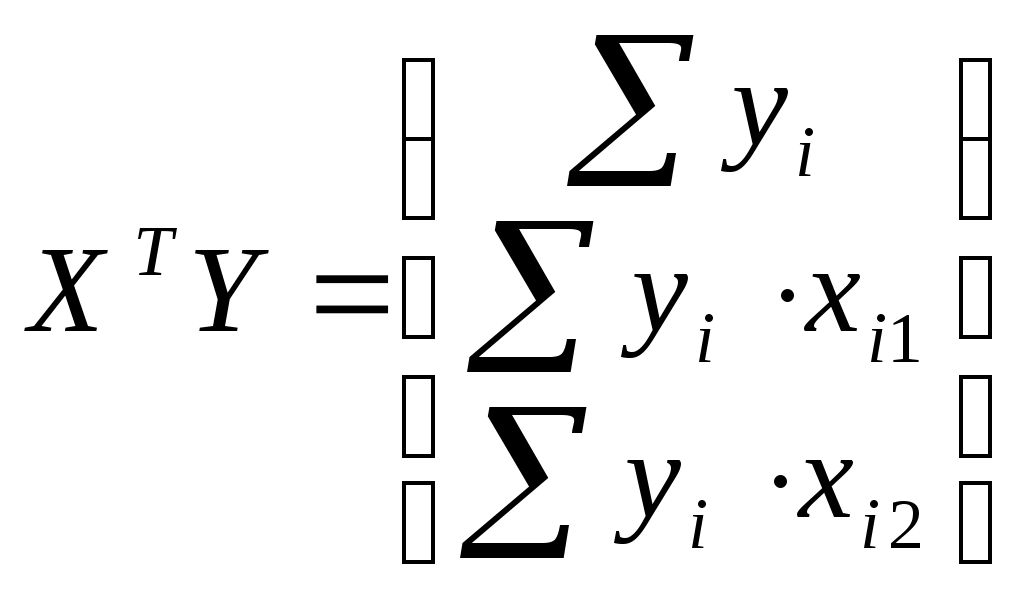
Для этого составим вспомогательную таблицу: (таблица 6)
i
|
yi
|
xi1
|
xi2
|
xi12
|
xi22
|
yi xi1
|
yi xi2
|
xi1xi2
|
1
|
8,3
|
6
|
88
|
36
|
7744
|
49,8
|
730,4
|
528
|
2
|
17,9
|
3
|
160
|
9
|
25600
|
53,7
|
2864
|
480
|
3
|
11,2
|
5
|
105
|
25
|
11025
|
56
|
1176
|
525
|
4
|
17,2
|
4
|
165
|
16
|
27225
|
68,8
|
2838
|
660
|
5
|
9,4
|
5,5
|
88
|
30,25
|
7744
|
51,7
|
827,2
|
484
|
6
|
15,9
|
4
|
145
|
16
|
21025
|
63,6
|
2305,5
|
580
|
7
|
6,8
|
7
|
95
|
49
|
9025
|
47,6
|
646
|
665
|
8
|
10,8
|
6
|
124
|
36
|
15376
|
64,8
|
1339,2
|
744
|
9
|
15,6
|
5
|
165
|
25
|
27225
|
78
|
2574
|
825
|
10
|
13,8
|
3,5
|
112
|
12,25
|
12544
|
48,3
|
1545,6
|
392
|
11
|
15,3
|
3
|
120
|
9
|
14400
|
45,9
|
1836
|
360
|
12
|
14,4
|
4,5
|
145
|
20,25
|
21025
|
64,8
|
2088
|
652,5
|
13
|
15,6
|
3,5
|
140
|
12,25
|
19600
|
54,6
|
2184
|
490
|
14
|
10,6
|
7
|
145
|
49
|
21025
|
74,2
|
1537
|
1015
|
15
|
11,2
|
5,5
|
120
|
30,25
|
14400
|
61,6
|
1344
|
660
|
16
|
13,4
|
4,5
|
132
|
20,25
|
17424
|
60,3
|
1768,8
|
594
|
Σ
|
207,4
|
77
|
2049
|
395,5
|
272407
|
943,7
|
27603,7
|
9654,5
|
 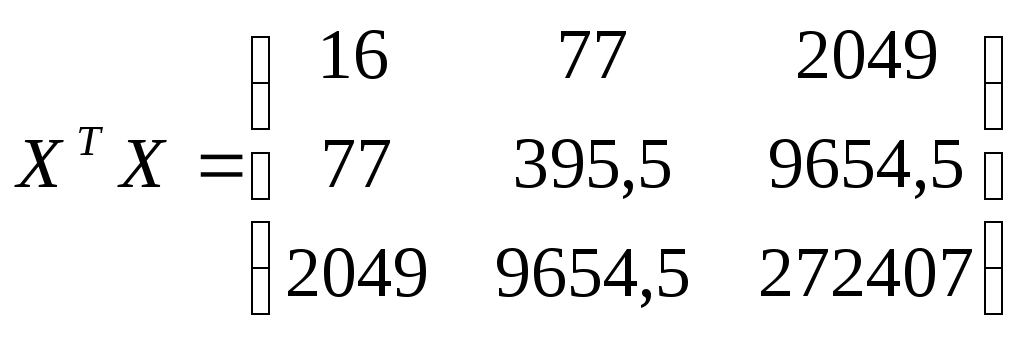 ; ; 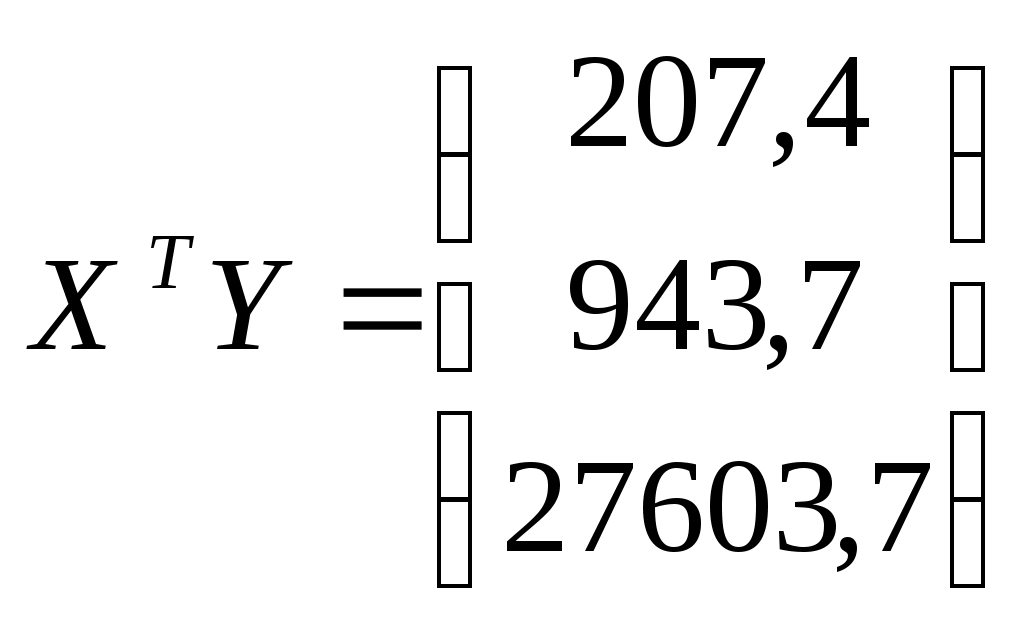
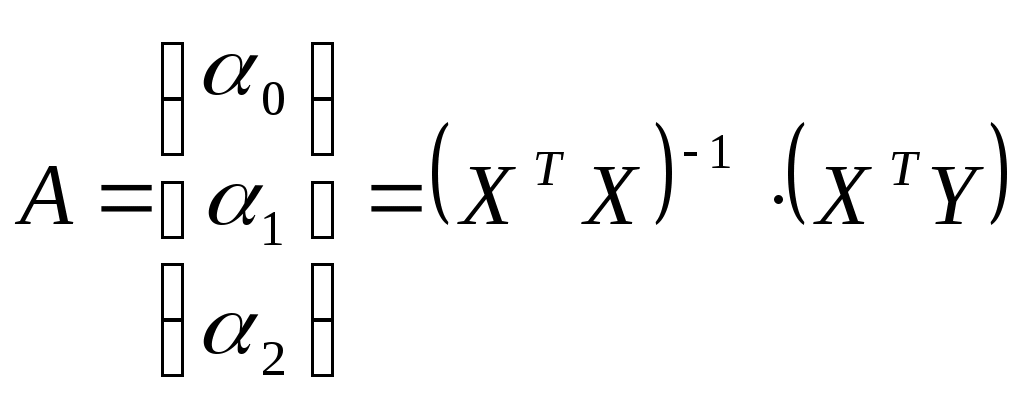
Найдем 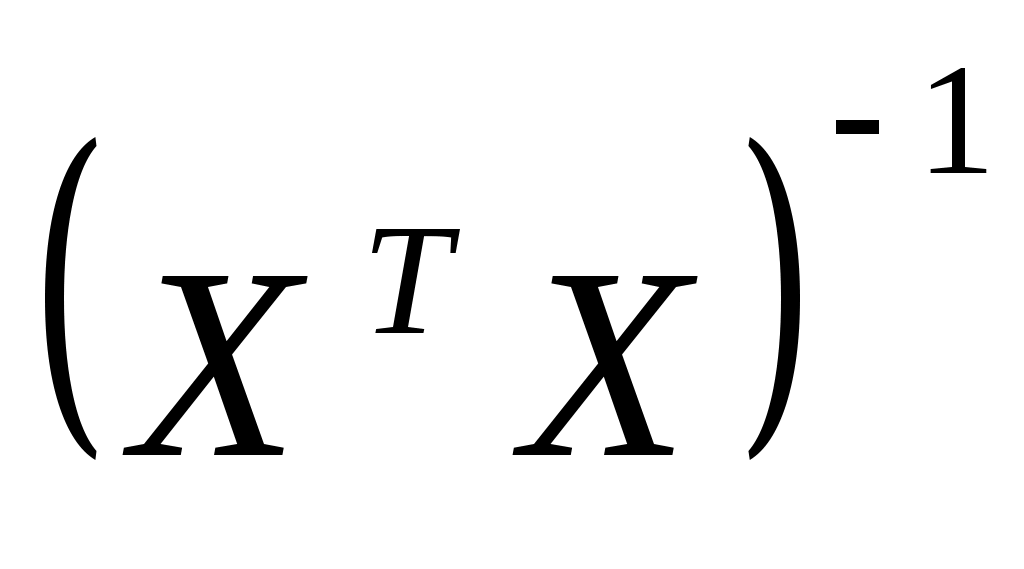 : :
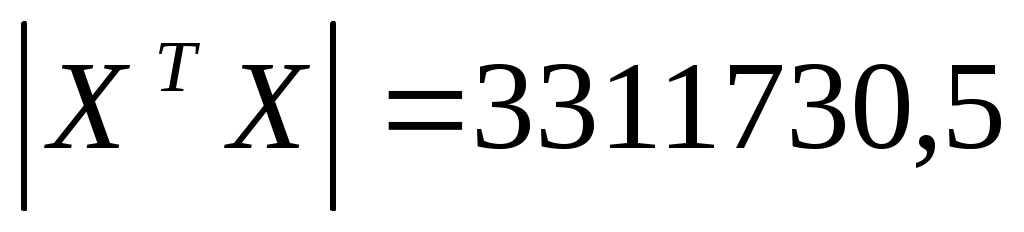
алгебраические дополнения:
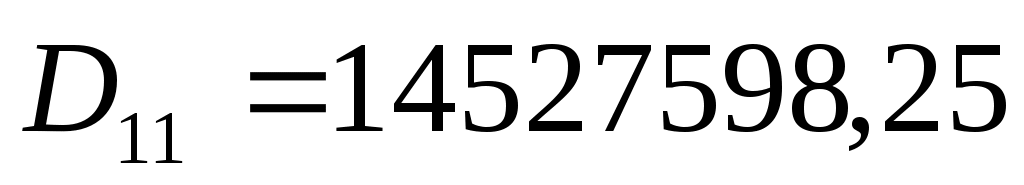 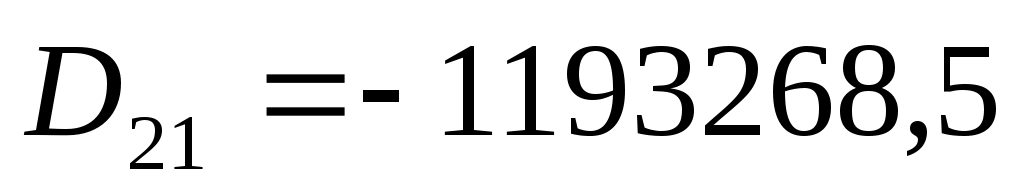 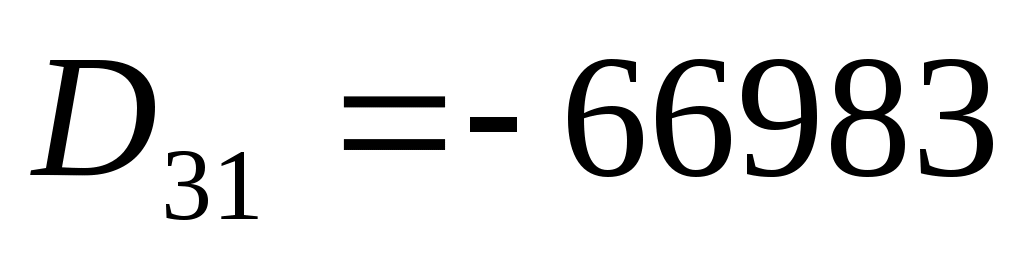
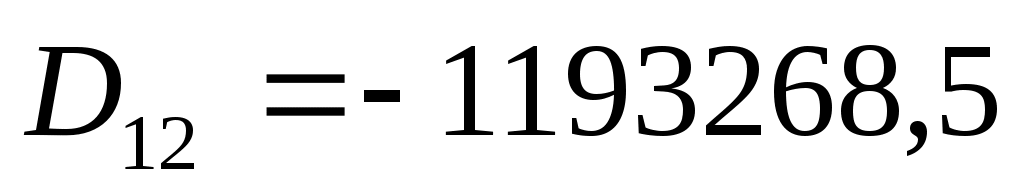 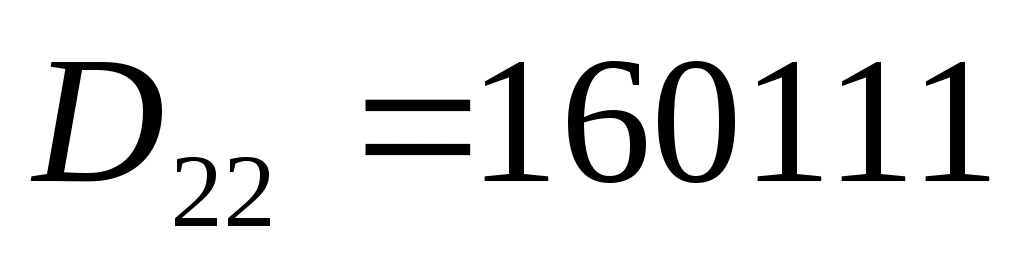 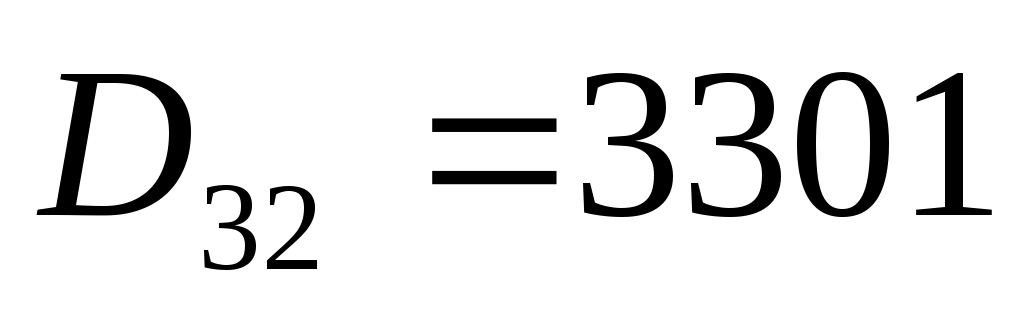
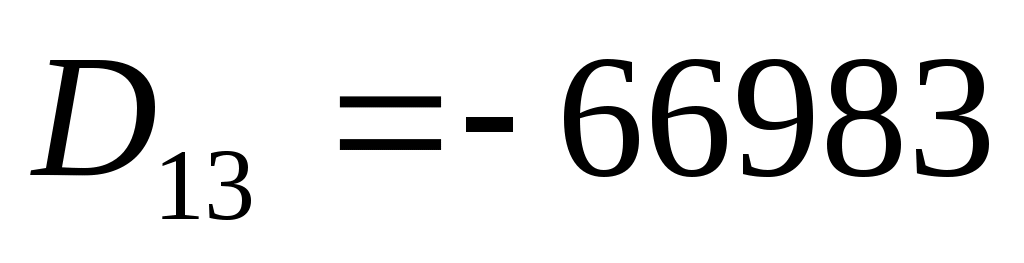 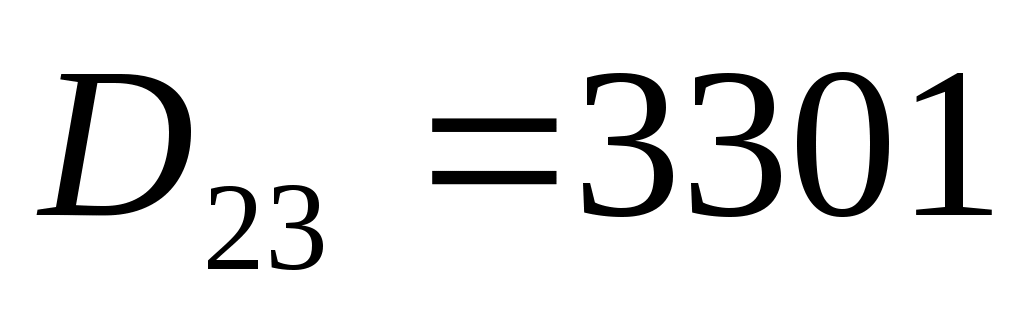 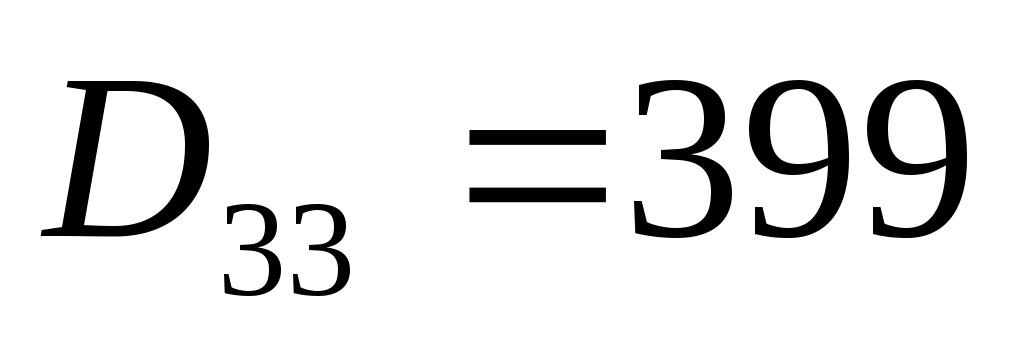
Тогда обратная матрица 
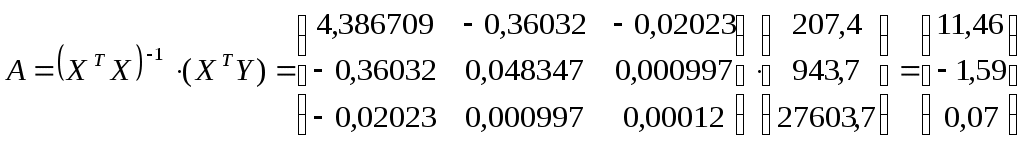 таким образом, получаем уравнение регрессии: таким образом, получаем уравнение регрессии:
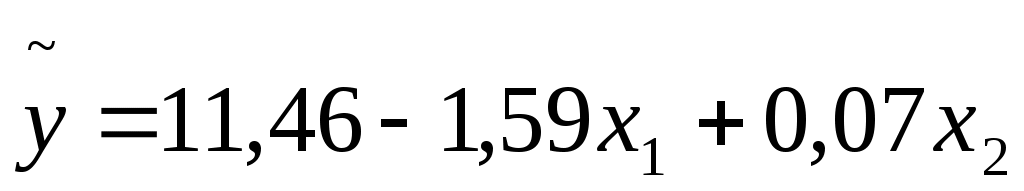 . .
2.2. Проверить статистическую значимость параметров и уравнения множественной регрессии с надежностью 0,9.
Для вычисления коэффициента детерминации составим таблицу: (таблица 7)
ỹi
|
ỹi -yi
|
(ỹi -yi )2
|
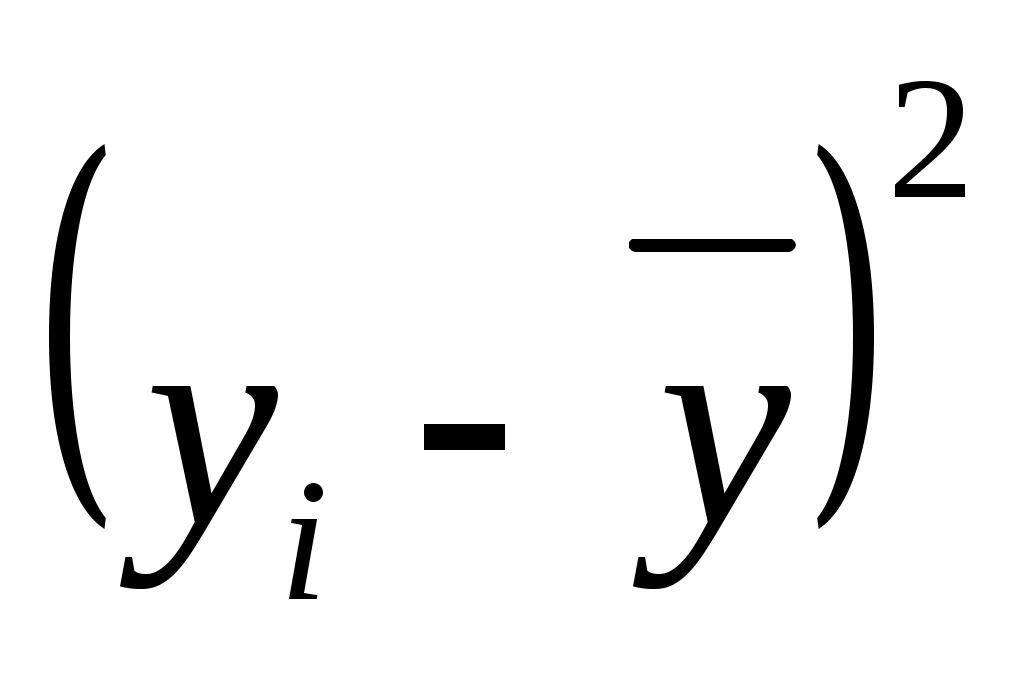
|
8,08
|
-0,22
|
0,0484
|
21,73891
|
17,89
|
-0,01
|
1E-04
|
24,37891
|
10,86
|
-0,34
|
0,1156
|
3,106406
|
16,65
|
-0,55
|
0,3025
|
17,95641
|
8,875
|
-0,525
|
0,275625
|
12,69141
|
15,25
|
-0,65
|
0,4225
|
8,628906
|
6,98
|
0,18
|
0,0324
|
37,97641
|
10,6
|
-0,2
|
0,04
|
4,676406
|
15,06
|
-0,54
|
0,2916
|
6,956406
|
13,735
|
-0,065
|
0,004225
|
0,701406
|
15,09
|
-0,21
|
0,0441
|
5,463906
|
14,455
|
0,055
|
0,003025
|
2,066406
|
15,695
|
0,095
|
0,009025
|
6,956406
|
10,48
|
-0,12
|
0,0144
|
5,581406
|
11,115
|
-0,085
|
0,007225
|
3,106406
|
13,545
|
0,145
|
0,021025
|
0,191406
|
|
|
1,63
|
162,18
|
Коэффициент корреляции 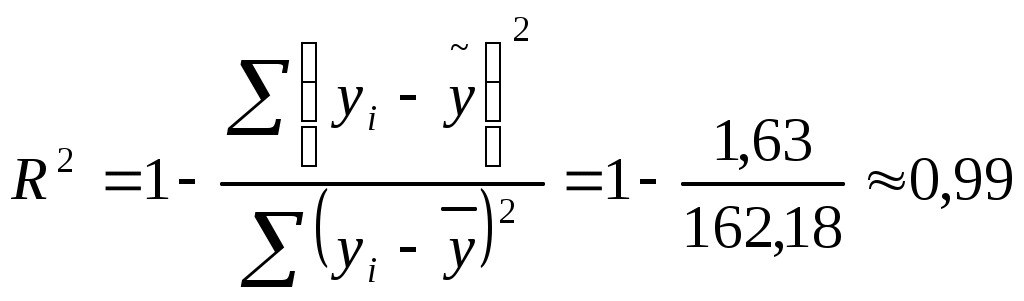
Следовательно, регрессия y на x1 и x 2 объясняет 99% колебаний значений у. Это свидетельствует о значительном суммарном влиянии независимых переменных x1 и x 2 на зависимую переменную у.
Качество уравнения множественной регрессии оценим с помощью F-теста, найдем
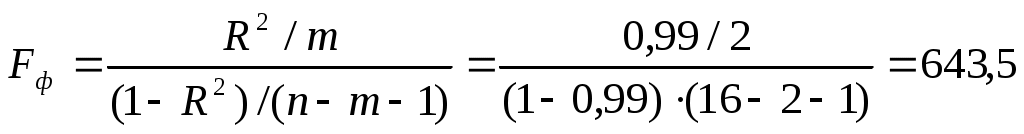
При уровне значимости 0,05 и 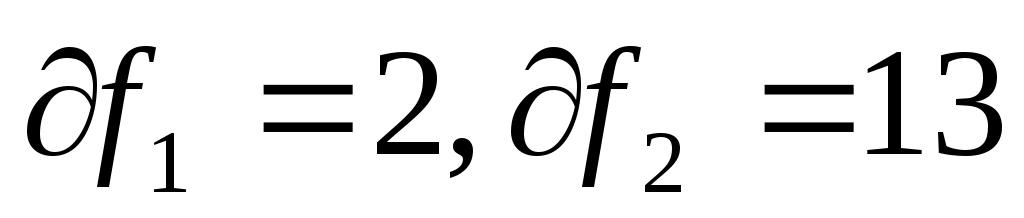 табличное значение Fm=3,81. Неравенство Fmф выполняется, гипотеза о незначимости коэффициентов регрессии отклоняется и признается статистическая значимость уравнения регрессии. табличное значение Fm=3,81. Неравенство Fmф выполняется, гипотеза о незначимости коэффициентов регрессии отклоняется и признается статистическая значимость уравнения регрессии.
2.3. Рассчитать точечный и интервальный прогноз среднего значения цены поступивших автомобилей возраста 3 года и мощностью 165 л.с. с доверительной вероятностью 0,9.
Точечный прогноз:
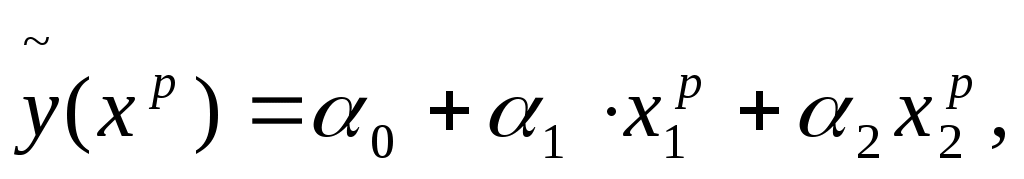 где где 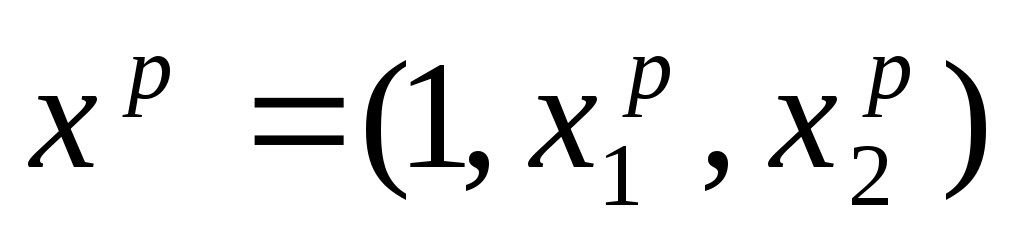 - вектор независимых переменных, для которого определяется прогноз. В нашем случае - вектор независимых переменных, для которого определяется прогноз. В нашем случае 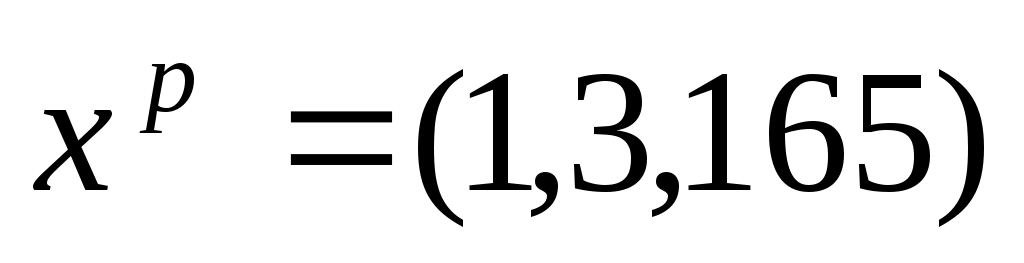
Тогда 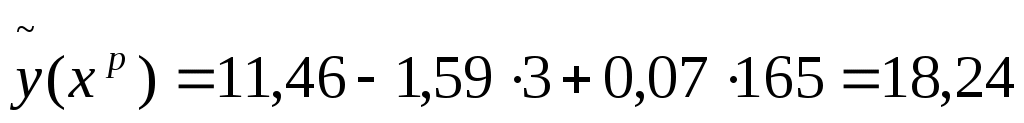
Интервальный прогноз:
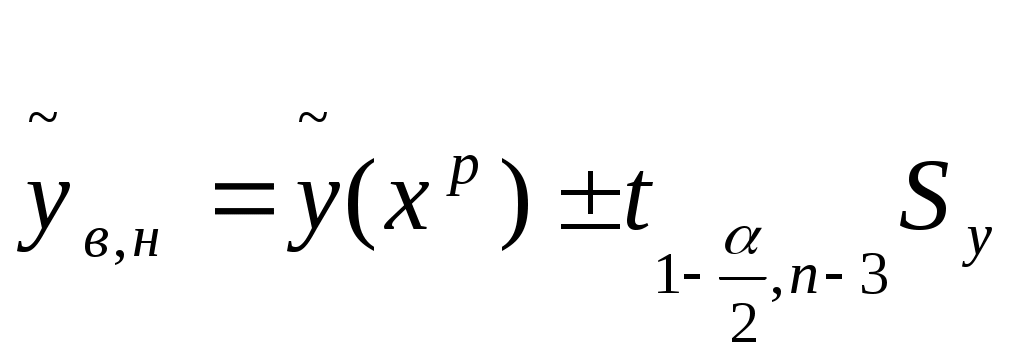 ; ; 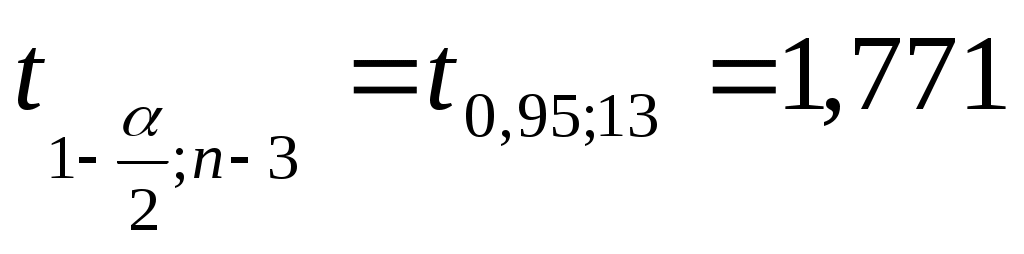
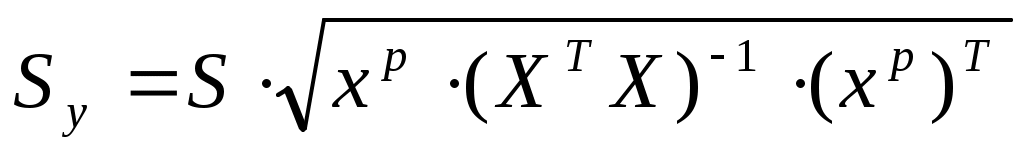 , где , где 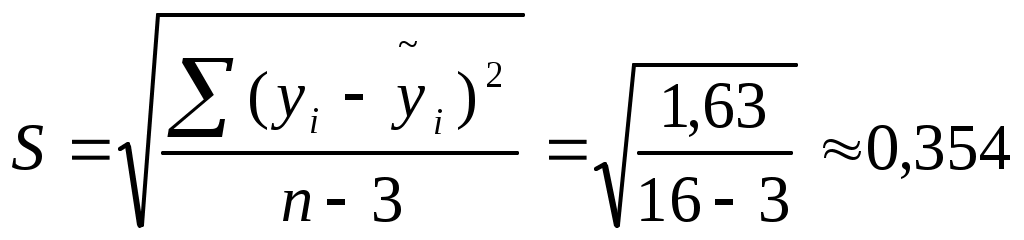
тогда 
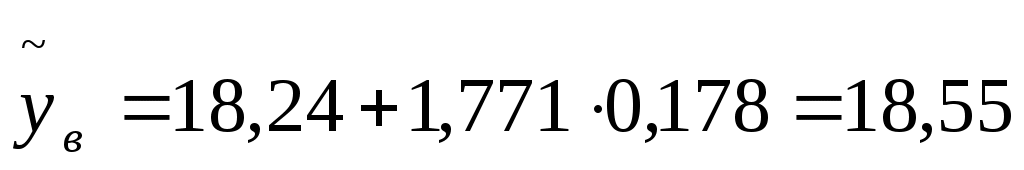
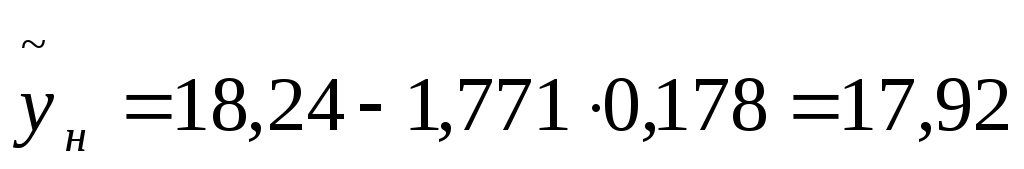
т.е. с надежностью 90% цена на поступившие автомобили попадет в интервал (17,92 ; 18,55).
3. Экономическая интерпретация.
Рассмотрим зависимость цены от возраста:
Так как 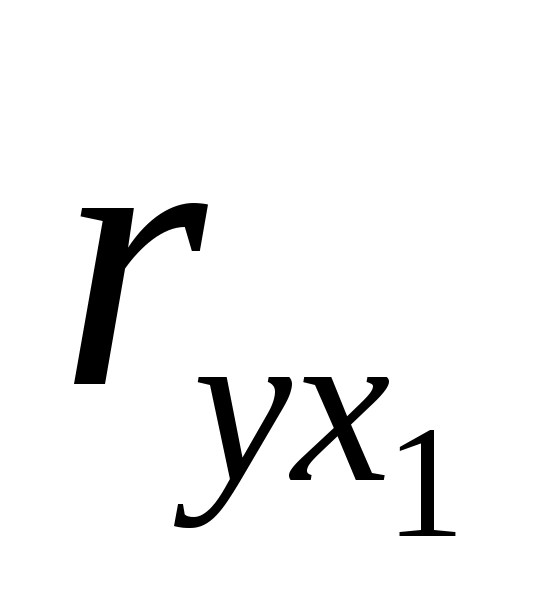 = -0,856 и проверка значимости показала его существенное отличие от 0, то есть основание утверждать, что между ценой автомобиля и его возрастом существует достаточно тесная отрицательная линейная зависимость, которая может быть отражена с помощью найденного уравнения регрессии = -0,856 и проверка значимости показала его существенное отличие от 0, то есть основание утверждать, что между ценой автомобиля и его возрастом существует достаточно тесная отрицательная линейная зависимость, которая может быть отражена с помощью найденного уравнения регрессии 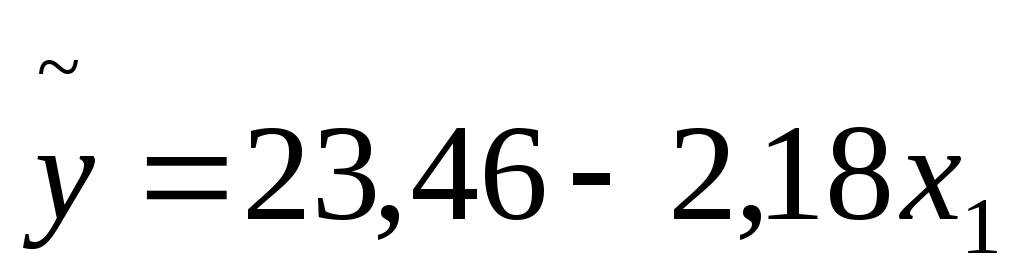 . .
Коэффициент 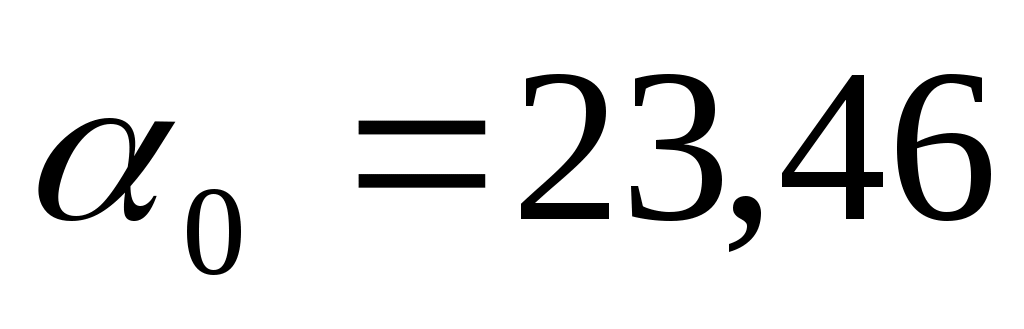 формально определяет цену нового автомобиля, т.е. когда формально определяет цену нового автомобиля, т.е. когда 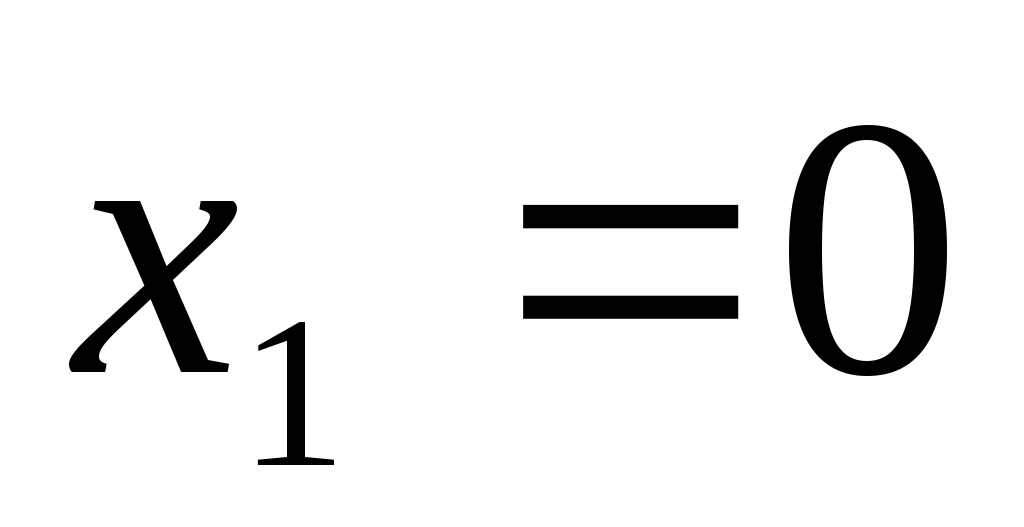 . .
Коэффициент 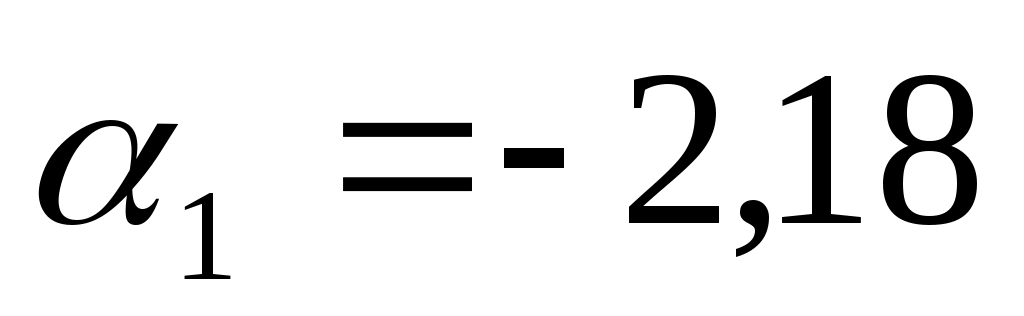 характеризует размер прироста цены, обусловленного приростом возраста на единицу, т.е. при увеличении возраста автомобиля на 1 год следует ожидать уменьшения цены на 2,18 тыс. у.е. характеризует размер прироста цены, обусловленного приростом возраста на единицу, т.е. при увеличении возраста автомобиля на 1 год следует ожидать уменьшения цены на 2,18 тыс. у.е.
Зависимость цены от мощности:
Так как 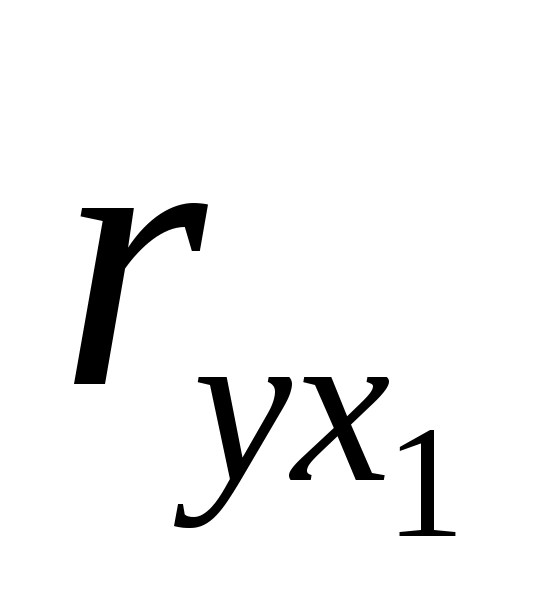 = 0,819 и проверка значимости показала его существенное отличие от 0, то есть основание утверждать, что между ценой автомобиля и его возрастом существует достаточно тесная линейная зависимость, которая может быть отражена с помощью найденного уравнения регрессии = 0,819 и проверка значимости показала его существенное отличие от 0, то есть основание утверждать, что между ценой автомобиля и его возрастом существует достаточно тесная линейная зависимость, которая может быть отражена с помощью найденного уравнения регрессии 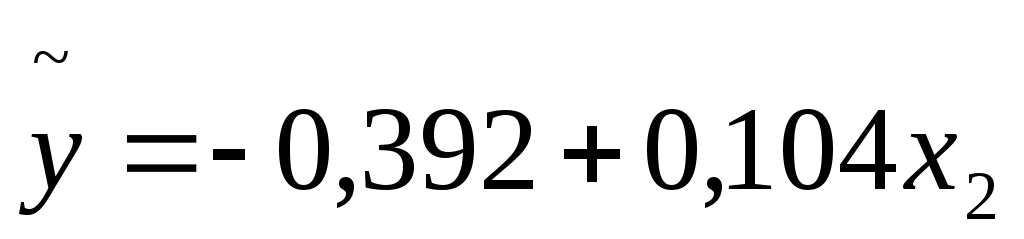 . .
Коэффициент 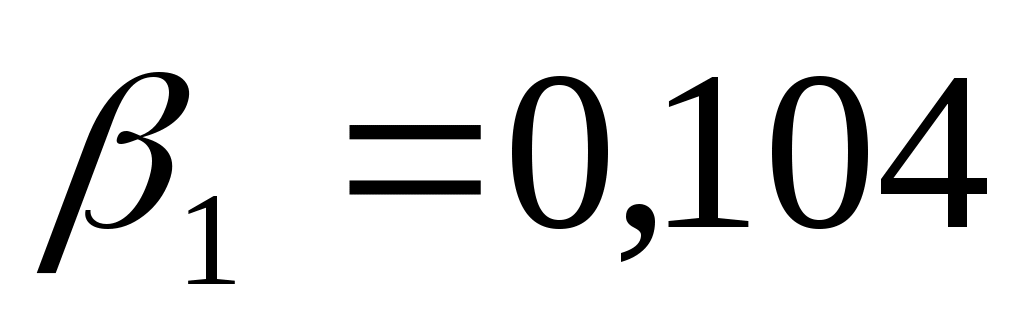 характеризует размер прироста цены, обусловленного приростом возраста на единицу, т.е. при увеличении мощности автомобиля на 1 л.с следует ожидать увеличения цены на 0,104 тыс. у.е. характеризует размер прироста цены, обусловленного приростом возраста на единицу, т.е. при увеличении мощности автомобиля на 1 л.с следует ожидать увеличения цены на 0,104 тыс. у.е.
В результате исследования зависимости объема цены от двух факторов – возраста и мощности двигателя получено уравнение множественной регрессии 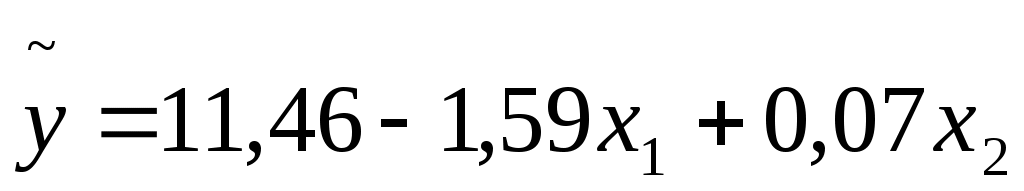
Коэффициент 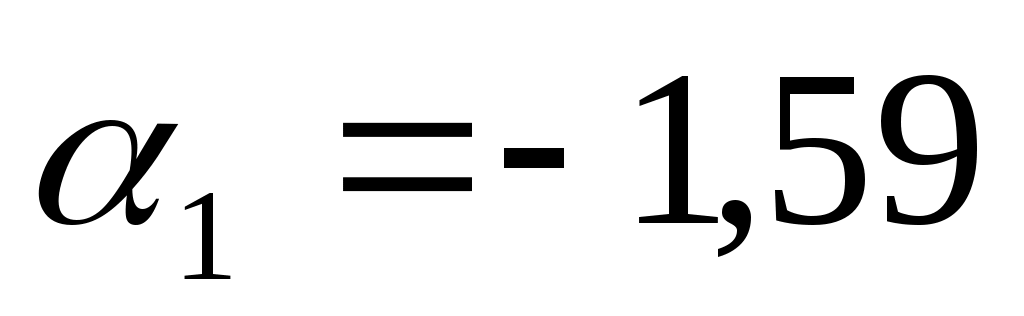 показывает, что при увеличении возраста на 1 год и неизменной мощности двигателя следует ожидать снижения цены автомобиля на 1,59 тыс. у.е. показывает, что при увеличении возраста на 1 год и неизменной мощности двигателя следует ожидать снижения цены автомобиля на 1,59 тыс. у.е.
Коэффициент 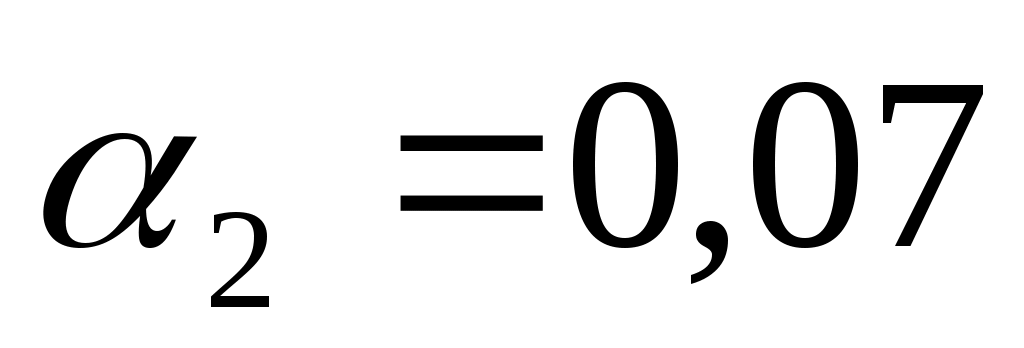 показывает, что при увеличении мощности на 1 л.с и неизменном возрасте следует ожидать увеличения цены автомобиля на 0,07 тыс. у.е. показывает, что при увеличении мощности на 1 л.с и неизменном возрасте следует ожидать увеличения цены автомобиля на 0,07 тыс. у.е.
|
|
|
 Скачать 0.98 Mb.
Скачать 0.98 Mb.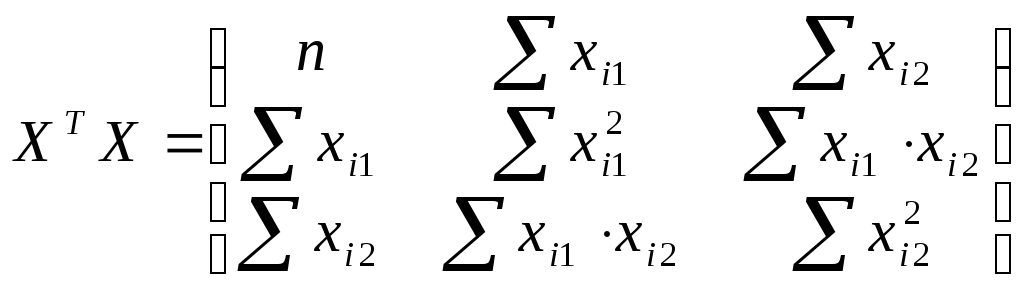 и
и 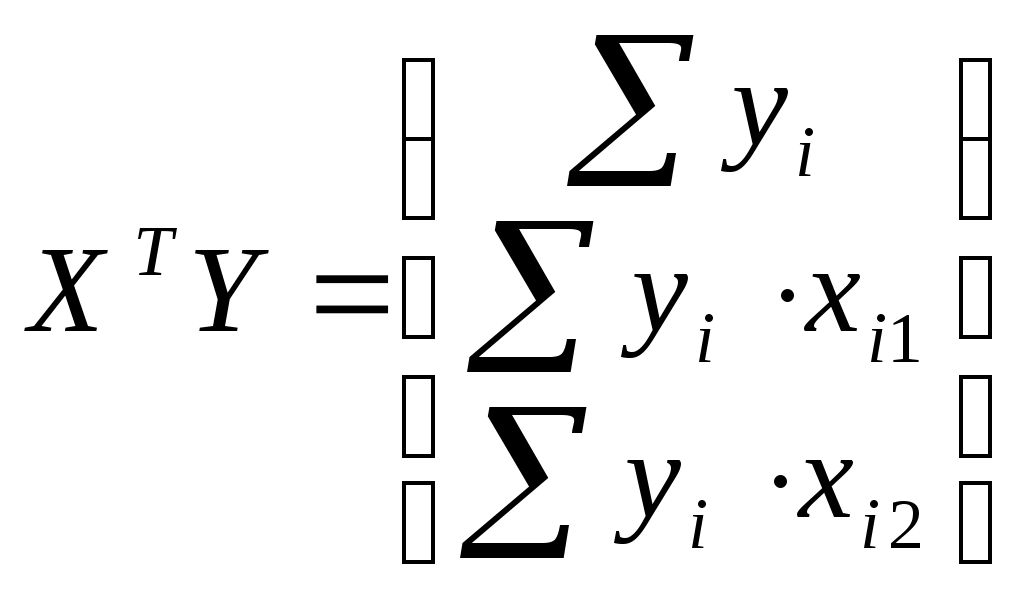
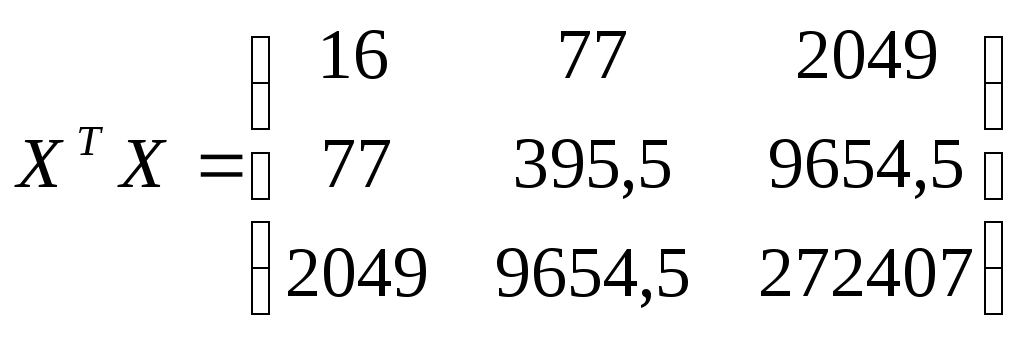 ;
; 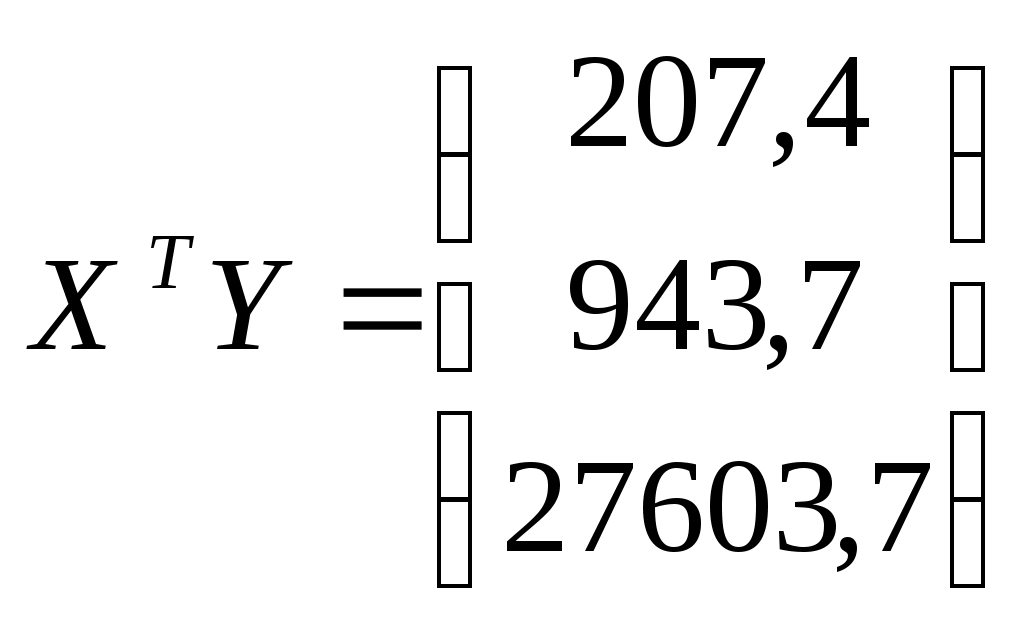
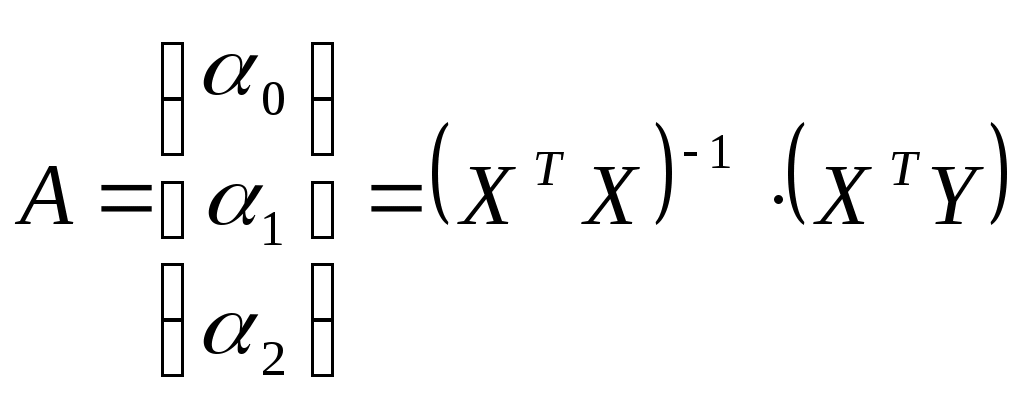
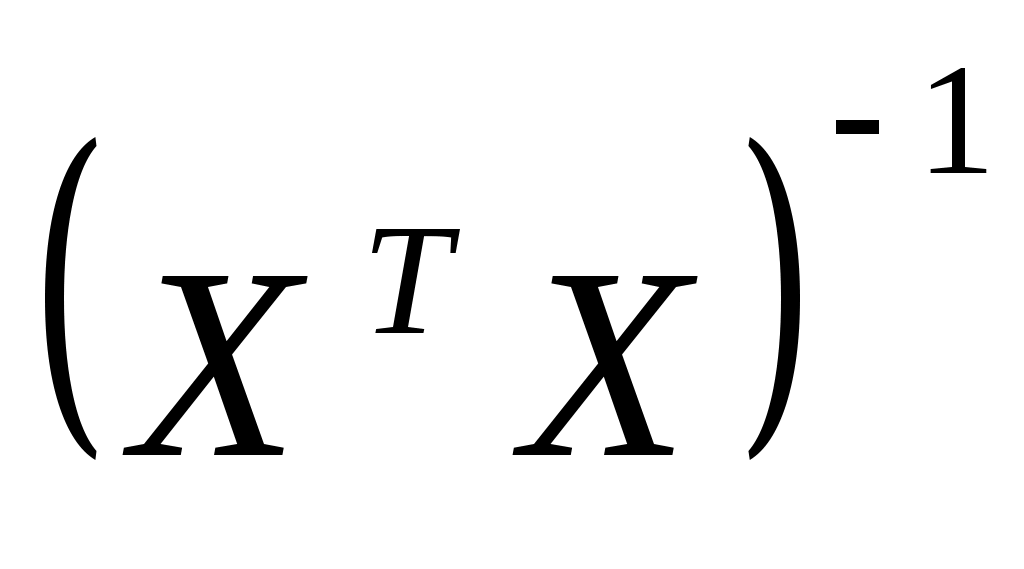 :
:
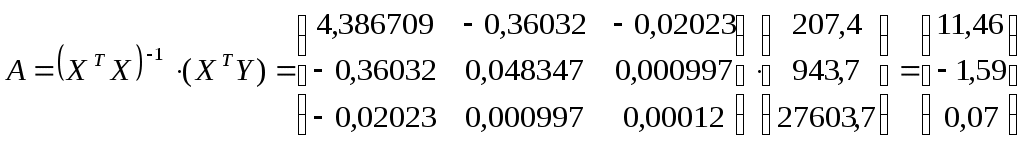 таким образом, получаем уравнение регрессии:
таким образом, получаем уравнение регрессии: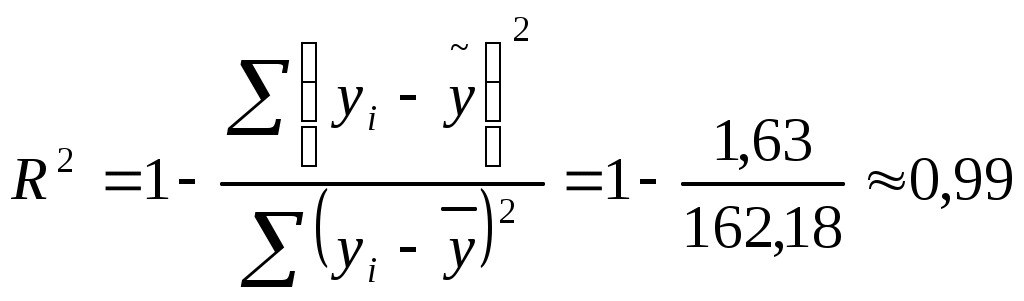
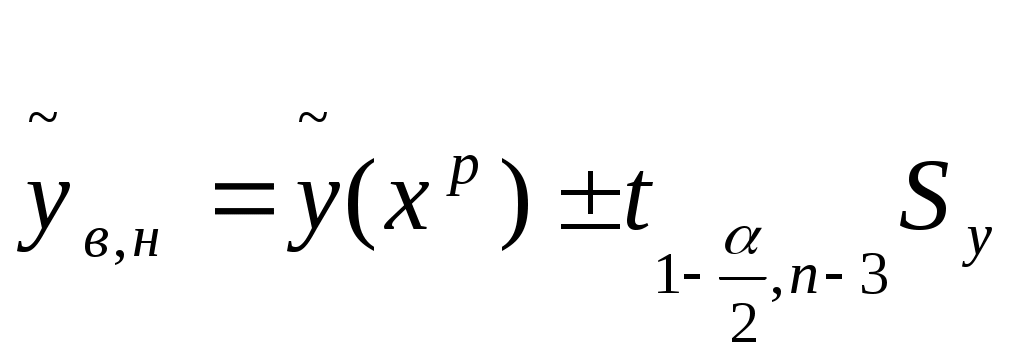 ;
;