курсовая по нтс. Задача 1
 Скачать 0.73 Mb.
|
|
График функции вероятности появления k дефектов.  График функции вероятности появления k и более дефектов.   Задача 4В результате измерений отказов n объектов, установлено среднее значение наработки на отказ Тcp, дисперсия—Dx. С какой вероятностью можно утверждать, что истинное среднее значение наработки на отказ не отклонится от найденной величины больше, чем на L? Исходные данные:
Решение: Расчет основывается на формуле для оценки параметра по результатам ограниченного числа испытаний.  Где tγ—параметр Стьюдента, определяемый из таблицы приложения 1 по значениям и k=n—1 степеней свободы, Т0n—среднее значение случайной величины; Т*0n—среднее значение случайной величины, измеренное при данных испытаниях; n—число опытов; σ* — среднее квадратическое отклонение: γ—доверительная вероятность. k=n—1= 61-1=60 σ*=  Для того, чтобы выполнялось Т0n = Т0n*± tγ •  Должно выполняться условие tγ • = Тcp• (L/100%)tγ=(Тcp•L•  )/ 100%• σ *= (78,54•3• )/( 100•2,45) = 7,511Из таблицы (1, приложение 3) по значениям k=60 и tr= 7,511 находим доверительную вероятность γ = 0,99 С вероятностью 0,99 можно утверждать, что среднее значение наработки на отказ не отклонится от найденной величины больше, чем на 3%. Задача 5Вероятность безотказной работы машины P(t) в период нормальной эксплуатации после t часов работы составляет Р. Определить интенсивность отказов λ. Построить график изменения P(t) и определить графически наработку на отказ. Исходные данные:
Решение: Так как рассматривается период нормальной эксплуатации машины, интенсивность отказов можно считать не изменяющейся величиной. Вероятность безотказной работы машины в период нормальной эксплуатации Р=е  Отсюда интенсивность отказов λ = -lnP/t = -ln0,93/1000 = 7,26•10-5
 Задача 6На испытания были поставлены 200 восстанавливаемых изделий. Статистика отказов по вариантам приведена в таблице. Необходимо построить гистограмму параметра потока отказов  (t), определить среднюю наработку до первого отказа Т0. Статистические данные об отказах восстанавливаемых изделий
Решение: В данном случае эксплуатируется восстанавливаемое изделие, основной характеристикой в условии мгновенного ремонта является параметр потока отказов  Построенную по сглаженной гистограмме кривую  (t) апроксимируем уравнением  .Найдем значения коэффициентов a,b и k:  ;  ; b=(0)- a=45 Коэффициент k определяется по любой точке на графике: (4000)=15•10-5 ; 15•10-5 = 9•10-5 + 36•10  ; k  Вычислим среднюю наработку до первого отказа Т  Задача 7Для технического объекта задана наработка на отказ Тоз. Требуется оценить безопасность объекта (по величине наработки на опасный отказ Т0) с доверительной вероятностью , если число отказов n, а суммарная наработка до наступления n отказов равна tn часов.
Исходные данные: Решение: Для решения задачи необходимо оценить надежность с учетом доверительных границ при k=2n=20 степеней свободы и =1- γ=1-0,95=0,05; /2=0,025 и 1—/2=0,975 по таблице приложения 4 находят  и  : 34 и 9тогда  гдеТ0- математическое ожидание наработки на опасный отказ. (2•350)/34  Т0 ( 2•350)/9 20,6 Т0 77,8Вывод: С доверительной вероятностью 0,95 наработка на отказ в часах будет лежать в интервале от 20,6 до 77,8 ч., так как Т03 не входит в этот интервал, объект не опасен. Задача 8
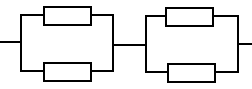
Решение:  где Рс (t) – вероятность безотказной работы системы.Рс (t) =(1-(1- Р1 ) • (1-Р2 )) • (1-(1-Р3 ) • (1-Р4 ))=(1-(1-Рi )2)2=(1-1+2Pi –Рi2)2= =4Рi2 -4Рi3+Рi4 Рi(t)= е   = -(2/λ) • е   +(4/3λ) • е  -(1/4λ) • е  =2/ λ-4/3 λ+1/4 λ=11/12 λ==11/12•0,79•10-4=11603,4 (ч) Вывод: Наработка на отказ составит 11603,4 ч.
Задача 9Восстанавливаемая система с показательным распределением времени безотказной работы и времени восстановления имеет коэффициент безопасности Kб. Определить вероятность нахождения системы в безопасном состоянии в момент времени t если наработка на опасный отказ То. Исходные данные:
Решение: Показательный закон распределения P(t) = е , в момент времени t: -t/КбТвГде Тв = (То/ Кб) – То = (850/0,84) – 850 = 161,9 ( ч.) Р(55)=0,84+(1-0,84) • е-20/(0,84•161,9)=0,978 Вывод: вероятность нахождения системы в безопасном состоянии в момент времени t=55 часов составляет 0,978. Задача 10На испытание поставлено N элементов. Число отказов n(∆ti) фиксировалось в каждом интервале времени испытаний ∆t=500 час. Необходимо определить вероятность безотказной работы  (∆t), частоту отказов  (∆t) и интенсивность отказов  (∆t), построить графики этих функций и найти среднюю наработку до первого отказа  .Исходные данные:
Решение:  (ti) = n(t +∆t)/ N; (ti) = 1-(ti);(ti) = n(∆t)/ N • ∆t; (ti) =
Продолжение табл.
= (0,5•143+1•83+1,5•72+2•51+2,5•46+3•41+3,5•30+4•26+4,5•21+5•21++5,5•22+6•23+6,5•45+7•63+7,5•53+8•30+8,5•16+9•14)•103/800 = = 3,629•103 (ч) Задача 11Для графа изменения состояния функционирования объекта, представленного на рис. 5.1, составить систему дифференциальных уравнений цепи Маркова, решить ее для стационарного процесса и определить наработку на опасный отказ (состояние 2) при заданных значениях интенсивностей ij, и допустимой вероятности опасного состояния Р2 . Каким должно быть время устранения опасного отказа, чтобы коэффициент опасности Кo принимал значения 0,001 и 0,0006.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
