КР стаитстика. 052 Статистика. Задача 2 Имеются следующие данные по предприятиям отрасли
 Скачать 156.18 Kb. Скачать 156.18 Kb.
|
|
Задача 2 Имеются следующие данные по предприятиям отрасли:
Для изучения зависимости между стоимостью основных производственных фондов и объемом продукции произведите группировку предприятий по стоимости основных производственных фондов, образовав четыре группы с равными интервалами. По каждой группе и в целом по совокупности подсчитайте: 1) число предприятий; 2) стоимость основных производственных фондов – всего и в среднем на одно предприятие; 3) стоимость продукции – всего и в среднем на одно предприятие; 4) фондоотдачу 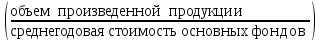 . .Результаты представьте в разработочной и групповой таблицах. Дайте анализ показателей таблицы и сделайте краткие выводы. Решение: Сделаем группировку по стоимости ОПФ. По условию образуем 4 группы с равными интервалами. Находим размер интервала: 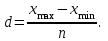 Где d – размер интервала; 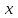 mах, ( mах, (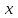 min) - максимальное (минимальное) значение группировочного признака в совокупности; min) - максимальное (минимальное) значение группировочного признака в совокупности;n - число единиц в совокупности. Тогда, 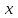 mах = 7 (млн. руб.); mах = 7 (млн. руб.);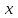 min = 1 (млн. руб.); min = 1 (млн. руб.);n = 4; d = (7-1)/4 = 1.5 (млн. руб.). Отграничим каждую группу предприятий, обозначив нижнюю границу каждого следующего интервала числом на 0,1 большим верхней границы предшествующего интервала. Получим следующие 4 группы: – [1,0-2,5] – [2,6-4,0] – [4,1-5,5] – [5,6-7,0] Занесем полученные данные в разработочную таблицу. Таблица 2
По данным таблицы 2 получим: Число предприятий в группах: I – 4 предприятия; II – 8 предприятий; III – 4 предприятия; IV – 4 предприятия; Всего 20 предприятий. Стоимость всех основных производственных фондов составляет 78,5 млн. руб., а в среднем на одно предприятие 78,5/20 = 3,925 млн. руб. Стоимость продукции – всего 96 млн. руб. и в среднем на одно предприятие 96/20 = 4,8 млн. руб. Рассчитаем средние показатели по каждой группе, данные занесем в аналитическую таблицу: Таблица 3
Фондоотдача в среднем на одно предприятие в группе составляет: 2,6/1,8 = 1,44 3,4/3,5 = 0,97 4,8/4,6 = 1,04 9,9/6,3 = 1,57 Результаты расчетов показывают, что с увеличением среднегодовой стоимости основных производственных фондов увеличиваются объемы произведенной продукции, т.е. чем выше стоимость ОПФ предприятия, тем больший объем продукции может быть произведен, а соответственно увеличится и фондоотдача. Задача 24 С целью изучения производительности труда работников предприятия произведено 10%-ное выборочное обследование (по методу механического отбора). Результаты представлены следующими данными:
Определите: 1) среднюю выработку изделий за смену одним работником; 2) дисперсию и среднее квадратическое отклонение; 3) коэффициент вариации; 4) с вероятностью 0,954 предельную ошибку выборки, а также интервал, в котором находится удельный вес всех работников предприятия, производящих за смену более 50 изделий. Сделайте выводы. Решение: В случае если в группах есть открытые интервалы, то величина интервала первой группы условно принимается равной величине интервала последующей, а величина интервала последней группы – равной величине интервала предыдущей:
1. Рассчитаем среднее кол-во изделий одного работника, применив формулу средней арифметической взвешенной: 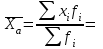 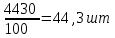 2. Расчет дисперсии и среднего квадратического отклонения проведем на основе данных следующей таблицы:
Для определения среднего квадратического отклонения используем формулу 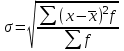 = =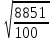 =9,41% =9,41%Так как среднее квадратическое отклонение есть корень квадратный из дисперсии, то дисперсия равна 88,51. Коэффициент вариации: 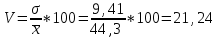 Колеблемость торговой площади в каждом магазине от среднего процента торговой площади довольно значительна, то есть средняя величина не совсем типична для данной совокупности. Определим с вероятностью 0,954 предельную ошибку выборки, а также интервал, в котором находится средний размер торговой площади всех магазинов. 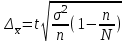 Коэффициент доверия при вероятности 0,954 равен 3. Генеральная совокупность N=1180, совокупность единиц, отобранных для выборочного наблюдения, n=20. 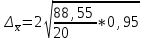 =36,9 =36,9Вычислим пределы стоимости для всех заводов: 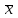 - -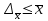 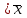 + +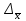 124,3-36,9 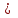 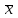 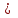 124,3+36,9 124,3+36,987,4% 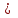 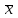 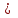 161,2% 161,2%С вероятностью 0,954 можно утверждать, что средняя торговая площадь колеблется в пределах от 87,4% до 161,2%. Задача 25 В результате 10%-ного выборочного обследования (по методу механического отбора) предприятий получены следующие данные: Решение: Для расчетов заменим интервалы их средними значениями. Величины первого и последнего открытых интервалов условно примем равными величинам второго и предпоследнего интервалов соответственно. Заполним вспомогательную расчетную таблицу:
1. Рассчитаем среднее значение численности персонала на одном предприятии по формуле средней арифметической взвешенной 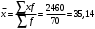 чел. чел.2. Рассчитаем дисперсию 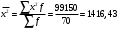 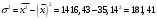 Среднее квадратическое отклонение равно 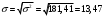 лет лет3. Рассчитаем коэффициент вариации: 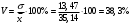 4. Предельная ошибка для генеральной средней вычисляется по формуле: 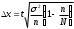 , где 2 - дисперсия, n - объем выборки, N - объем генеральной совокупности, а t - коэффициент доверия, зависящий от вероятности, с которой делается утверждение (при P=0,954 t=2). Т.к. выборка 10% -ная, то отношение , где 2 - дисперсия, n - объем выборки, N - объем генеральной совокупности, а t - коэффициент доверия, зависящий от вероятности, с которой делается утверждение (при P=0,954 t=2). Т.к. выборка 10% -ная, то отношение 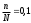 . Подставим известные данные в формулу: . Подставим известные данные в формулу: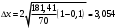 Пределы для генеральной средней задаются неравенствами: 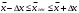 Таким образом, интервал, в котором находится среднее значение численности работников всех предприятий, будет 35,14 - 3,054 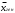 35,14 + 3,054 35,14 + 3,05432,086 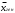 38, 194 38, 194Выводы: среднее значение численности работников на одно предприятия равно 35,14 чел. Колеблемость численности от ее среднего значения, определяемая коэффициентом вариации, составляет 38,3%. Т.к. это значение больше 30%, то полученное значение средней численности не является типичным для данной совокупности. С вероятностью 0,954 можно утверждать, что средняя численность работников всех предприятий лежит в пределах от 32,086 до 38, 194 человек. Задача 49 Данные о реализации продуктов и ценах составили:
Определите: 1) индивидуальные и общий индексы соотношения цен частной и муниципальной форм торговли; 2) сумму переплат (экономии) населения в результате покупки продуктов в частных предприятиях. Сделайте выводы. Решение: 1) Индивидуальные индексы цен рассчитываются как отношение цен муниципальной и частной торговли: 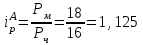 или 112,5% или 112,5%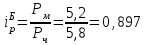 или 89,7% или 89,7%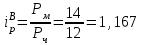 или 116,7% или 116,7%Общий индекс цен рассчитываем по формуле: 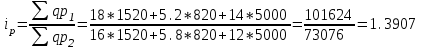 или 139,07% или 139,07%2) Сумма переплат (экономии) населения в результате покупки продуктов в частных предприятиях: 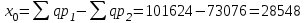 руб. руб.Таким образом, сумма переплат значительно высока и составляет 39,07%. Задача 55 Данные о фондоотдаче и износе основных фондов по десяти предприятиям:
Выявите наличие, направление и форму связи между фондоотдачей и износом основных фондов, используя графический метод. Представьте связь в виде линейного уравнения регрессии, проанализируйте параметры уравнения регрессии и оцените тесноту связи, рассчитав линейный коэффициент корреляции. Сделайте выводы. Решение: Корреляционную зависимость для наглядности можно изобразить графически. Для этого, имея 10 взаимосвязанных пар значений x и y и пользуясь прямоугольной системой координат, каждую такую пару изображают в виде точки на плоскости с координатами x и y (рис.) 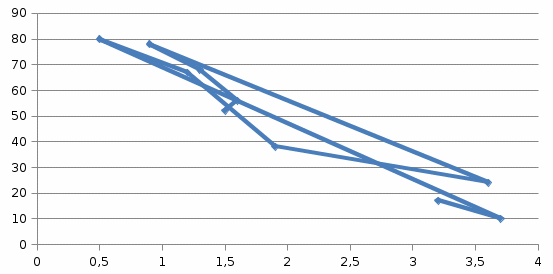 Рис.1. Графический метод Соединяя последовательно нанесенные точки, получают ломаную линию, именуемую эмпирической линией регрессии. В нашей задаче эта линия не похожа на восходящую прямую, что позволяет выдвинуть гипотезу об отсутствии зависимости между величиной фондоотдачи и коэффициентом износа. Метод сопоставления параллельных рядов. Единицы наблюдения располагают по возрастанию значений факторного признака х и затем сравнивают с ним (визуально) поведение результативного признака у. В нашей задаче в большинстве случаев по мере увеличения значений x увеличиваются и значения y. 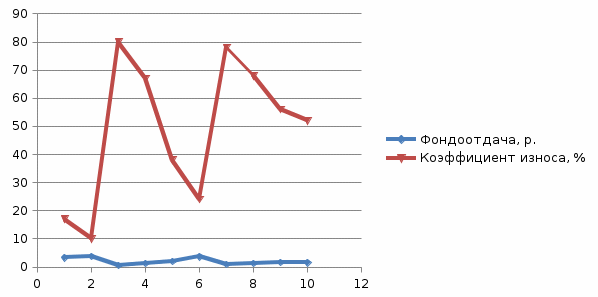 Рис.2. Метод сопоставления параллельных рядов На основании поля корреляции можно выдвинуть гипотезу (для генеральной совокупности) о том, что связь между всеми возможными значениями X и Y носит линейный характер. Задача 68Данные по торговой фирме за два периода:
Определите: 1) среднюю выработку одного работника за каждый период в действующих и сопоставимых ценах; 2) индексы средней выработки в действующих и сопоставимых ценах; 3) абсолютный прирост оборота – всего, в том числе за счет изменения цен, средней выработки и численности работников. Сделайте выводы. Решение: Выработка - это сумма товарооборота, приходящаяся на одного работника: 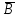 = =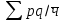 По нашим данным выработка в базисном периоде составила: 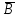 0= 0=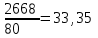 тыс. руб., тыс. руб.,в отчетном периоде: 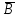 1= 1=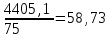 тыс. руб. тыс. руб.Чтобы исключить влияние изменения цен, вычислим выработку в сопоставимых ценах: 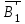 = =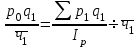 = =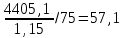 тыс. руб. тыс. руб.Общий прирост товарооборота в отчетном периоде по сравнению с базисным составил: 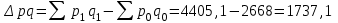 тыс. руб. тыс. руб.в том числе: за счет изменения выработки: 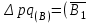 - -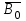 ) ) 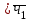 = (58,73-33,35) *75=1903,5 тыс. руб. = (58,73-33,35) *75=1903,5 тыс. руб.за счет изменения численности работников: 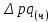 = ( = (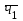 - -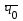 ) * ) *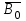 = (75-80) *33,35= - 166,75 тыс. руб. = (75-80) *33,35= - 166,75 тыс. руб. Задача 87 Имеются данные об оптовой продаже продовольственных товаров за два периода:
Исчислите: 1) общие индексы оборота в действующих и сопоставимых ценах и индекс цен; 2) абсолютную сумму изменения оборота – всего, в том числе за счет динамики цен и физического объема продажи товаров. Проверьте правильность расчета общих индексов по их взаимосвязи. Сделайте выводы. Решение: Общий индекс оборота продовольственных товаров в действующих ценах:  или 51% или 51% Индекс цен можно найти, поделив индекс товарооборота в действующих ценах на индекс товарооборота в сопоставимых ценах:  Рассчитаем абсолютную сумму изменения оборота – всего, в том числе за счет динамики цен и физического объема: В том числе за счет роста цен: за счет динамики физического объема: Товарооборот отчетного периода вырос на 180 тыс. руб., в том числе за счет роста цен на 345 тыс. руб., но за счет физической массы уменьшился на 165 тыс. руб. Список литературы 1. Социально-экономическая статистика : учеб. пособие / Я.С. Мелкумов. — 2-е изд., перераб. и доп. — М. : ИНФРА-М, 2018. — 186 с. — (Высшее образование: Бакалавриат). - Режим доступа: http://znanium.com/go.php?id=912522 2. Гужова О.А. Статистика в управлении социально-экономическими процессами : учеб. пособие / О.А. Гужова, Ю.А. Токарев. — М. : ИНФРА-М, 2017. — 172 с. — (Высшее образование: Бакалавриат). — www.dx.doi.org/10.12737/21034. - Режим доступа: http://znanium.com/go.php?id=556718 3. Статистика: учебник / В.В. Глинский, В.Г. Ионин, Л.К. Серга [и др.] ; под ред. В.Г. Ионина. — 4-е изд., перераб. и доп. — М. : ИНФРА-М, 2018. — 355 с. — (Высшее образование: Бакалавриат). — www.dx.doi.org/10.12737/25127. - Режим доступа: http://znanium.com/go.php?id=941774 Экономическая статистика : учебник / под ред. Ю.Н. Иванова. — 5-е изд., перераб. и доп. — М. : ИНФРА-М, 2018. — 584 с. + Доп. материалы [Электронный ресурс; - Режим доступа: http://www.znanium.com]. — (высшее образование: Бакалавриат). — www.dx.doi.org/10.12737/7728. - Режим доступа: http://znanium.com/go.php?id=952161 Экономическая статистика. Практикум : учеб. пособие / Ю.Н. Иванов, Г.Л. Громыко, А.Н. Воробьев [и др.] ; под ред. д-ра экон. наук, проф. Ю.Н. Иванова. — М. : ИНФРА-М, 2018. — 176 с. — (Высшее образование: Бакалавриат). — www.dx.doi.org/10.12737/23950. - Режим доступа: http://znanium.com/go.php?id=952160 СТАТИСТИКА (теория статистики, социально-экономическая статистика) : сборник задач / ЧОУ ВО Центросоюза РФ СибУПК;сост.С.С.Донецкая. - Новосибирск, 2016. - 164с. : ил. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||