Текстовая задача и её роль в обучении математике. Задача и её роль в обучении математике
 Скачать 62.7 Kb. Скачать 62.7 Kb.
|
|
Текстовая задача и её роль в обучении математике В методике обучения математике младших школьников используемые арифметические задачи чаще других принято называть термином "текстовые задачи". Такой же термин применяется и в курсе теоретических основ математики. Задачей называется требование определить числовое значение искомой величины по известным числовым значениям других величин и зависимостям, выраженным в словесной форме, которые связывают все эти величины между собой. Чтобы выяснить, как построена текстовая задача, рассмотрим пример из начального курса математики: З а д а ч а. Туристы за два дня прошли 44 км, двигаясь с одинаковой скоростью. В первый день они были в пути 6 ч, а во второй 5ч. Какое расстояние прошли туристы в каждый из этих дней? В данной задаче речь идет о туристах и относительно них имеем такие утверждения: 1. Туристы за два дня прошли 44км. 2. Они в каждый день двигались с одинаковой скоростью. 3. В первый день они были в пути 6 ч. 4. Во второй день они были в пути 5 ч. В этих утверждениях дается числовой материал задачи и зависимость между ними. Их принято называть условиями задачи. Предложение "Какое расстояние прошли туристы в каждый из этих дней?" принято называть требованием задачи. В методической литературе и в школьной практике вместо этого термина чаще используется термин "вопрос задачи". Условия задачи должны соответствовать уровню математической подготовки учащихся. Они должны быть сформулированы точно, ясно и немногословно. Требование задачи может быть выражено побудительным предложением (Найти периметр.) или вопросительным (Чему равен периметр?). Оно должно быть сформулировано ясно, точно и вытекать из содержания задачи. Все текстовые задачи делятся на простые и составные. Простой задачей называется такая, которая решается с помощью одного действия. Например: "У пруда росло 9 осин и берез. Осин было 4. Сколько было берез?". Задача решается одним действием - вычитанием. Составной задачей называется задача, которая решается при помощи двух или более действий. Например: "В школьной столовой было 16 кг рисовой крупы и 10 кг гречневой. За день израсходовали 6 кг крупы. Сколько крупы осталось в столовой?". Решается двумя действиями - сложением и вычитанием. Обычно в задачах число зависимостей соответствует числу данных и искомых, т.е. заданных условий столько, сколько необходимо и достаточно для её решения. Такие задачи называются определенными (например, вышеприведенные задачи). Если же такого соответствия нет, то: при недостатке условий для получения решения, задача называется недоопределенной (с недостающими данными), а при их избытке, когда некоторые их них не имеют значения для решения - переопределенной (с лишними данными, с избыточными данными). Простые задачи в зависимости от математических действий, с помощью которых они решаются, можно разделить на различные виды: задачи на сложение, вычитание, умножение и деление. Можно классифицировать и в зависимости от понятий, которые формируются при их решений (например, задачи на разностное отношение). В научно-методической литературе термин "решение задачи" понимают в разных смыслах. Наиболее распространенным являются: 1) решением задачи называют результат, т.е. ответ на вопрос задачи; 2) решением задачи называют процесс нахождения этого ответа, т.е. вся деятельность человека, решающего поставленную задачу. Роль задач в обучении математике в основном сводится к реализации трех целей обучения: образовательных, воспитательных и практических. С другой стороны, для учителя задача выполняет еще и контролирующую функцию, которая определяет уровень знаний учащихся, их способности к самостоятельному изучению математики. В решении задач наиболее важным является обучение учащихся поиску решения и его реализации. Именно здесь у них развивается логическое мышление, их математические способности, умения связать математику с реальной жизненной ситуацией, применять полученные теоретические знания в конкретной ситуации и т.п. Другими словами, основная роль решения задач - это развитие учащихся, при котором математическая задача служит как бы инструментом. В методике обучения решению каждого вида задач учитель должен предусмотреть следующие ступени: 1) подготовительная работа к решению задач; 2) ознакомление с решением задачи; 3) закрепление умения решать задачи. О подготовительной работе к решению задач остановимся далее, при рассмотрении конкретных видов задач. В методике работы на второй ступени выделяются следующие этапы: 1. Восприятие и осмысление задачи. 2. Поиск плана решения задачи. 3. Выполнение плана решения задачи. 4. Проверка решения задачи. \ Конец формы §2. Восприятие и осмысление задачи Решение текстовой задачи начинается с её восприятия и осмысления. На этом этапе основной целью ставится понимание задачи, т.е. уметь представить жизненную ситуацию, отраженную в задаче за счет установления смысла каждого слова, предложения, выделения условия и искомого, за счет воображения и представления. 1. Правильное чтение задачи. 2. Представление ситуации, описанной в задаче. 3. Разбиение текста задачи на смысловые части. 4. Переформулировка текста задачи (замена термина содержательным описанием, В задаче: "Пешеход со скоростью 4 км/ч шел 3 часа. Какое расстояние он прошел?" замена термина скоростью на содержательное его описание "расстояние, пройденное в 1 час" приводит к тексту: "Пешеход в каждый час проходил 4 км. Какое расстояние он прошел за 3 часа?" облегчает нахождение его решения. В первой задаче ученик опирается на правило: "Чтобы найти расстояние, надо скорость умножить на время", а во второй на понятие умножения: "Если в 1 час проходит 4 км, а за 3 часа будет 4 км три раза, т.е. 4·3=12 (км)". Это особенно важно для средних и слабых учащихся. 2) Замена содержательного описания термином. Прием используется для дальнейшего закрепления знания терминов, понятий и т.п. В задаче: "Туристы прошли на лодках 28 км за 4 ч, проходя в каждый час одно и то же расстояние. С какой скоростью двигались туристы на лодках?" такая переформулировка: "Туристы прошли на лодках 28 км за 4 час, с одинаковой скоростью. С какой скоростью двигались туристы на лодках?" ускоряет усвоение понятия скорости и правила её нахождения. 3) Исключение или добавление части текста, не влияющей на результат решения. З а д а ч а: "Из двух сел - Антоновки и Петровки, находящихся на расстоянии 20 км, одновременно навстречу друг другу вышли два пешехода: Коля и Саша. Коля шел со скоростью 4 км/ч, а Саша - 6 км/ч. Через сколько часов они встретились?" - в такой формулировке предлагается для повышения интереса учащихся к математическому материалу. Переформулировкой: "Из двух сел, находящихся на расстоянии 20 км, одновременно навстречу друг другу вышли два пешехода. Один шел со скоростью 4 км/ч, другой - 6 км/ч. Через сколько часов они встретились?" мы, исключив часть текста, облегчаем восприятие математического содержания. Обратный процесс, т.е. добавление "лишних" частей (названий населенных пунктов, имена каких-либо персонажей и т.п.) помогает учителю "сухую математическую" задачу превратить в реальную жизненную ситуацию и тем самым заинтересовать ученика в ее решении. В таких случаях ему интересно, допустим, кто же шел быстрее, кто прошел больше и т.п. Ему интересно узнать реальное явление: в этом случае он "не решает" задачу (как он сам думает!), а выясняет реальную ситуацию. Незаметно для ученика математика становится инструментом познания реальной действительности. 4) Замена числовых данных другими. При изучении аналогии мы рассмотрели пример, где замена числовых данных облегчает решение основной задачи . 5) Замена связей между числовыми данными задачи. (См. гл.3, § 9: "Использование взаимообратных опорных схем"). Для переформулировки текста задачи также можно использовать: замену некоторых слов синонимами или другими словами, близкими по смыслу; применение порядка слов, предложений; дополнение текста пояснениями; замена числовых данных буквенными и наоборот и другие. Результат переформулировки может быть отражен в краткой записи задачи или же выражен в устной форме. Обучение переформулировке текста можно начинать еще при рассмотрении простых задач, когда уже учащиеся умеют выделять условие и вопрос задачи. Первоначальное ознакомление с этим приемом может быть предъявлено в результате такой беседы: - Ребята, при решении многих задач я предлагаю вам рассказать содержание, выделить условие и вопрос задачи. В будущем нам придется решать более сложные задачи. Чтобы правильно и быстро решить задачу, надо хорошо понять все, что в ней сказано. Это самое главное условие. Чтобы облегчить понимание задачи, мы сегодня будем учиться переформулировке задачи, т.е. будем говорить задачу по-другому. Для этого иногда будем заменять одни слова другими, убирать или добавлять слова. А теперь рассмотрим задачу (читают по учебнику): "У Романа было 5 шариков, а стало на 2 шарика больше. Сколько шариков стало у Романа?" Что такое 5? (5 шариков было у Романа.) Как вы понимаете "стало на 2 больше"? (Ему дали еще 2 шарика.) А теперь я задачу читаю так: "У Романа было 5 шариков. Ему подарили еще 2 шарика. Сколько шариков стало у Романа?" Что я изменил? (Вместо "стало на 2 больше" прочитали "подарили 2 шарика".) Вот, ребята, мы с вами задачу прочитали по-другому, переформулировали. Этот термин, кто может, пусть запомнит. При обучении переформулировке большую помощь оказывают задачи с недостающими или лишними данными. 5. Моделирование условия задачи. Моделирование условия задачи понимается как умение переходит от текста (словесная модель задачи) к представлению описанной ситуации (мысленная модель) и от нее к записи с помощью математических символов (знаково-символическая модель). Модель помогает понять и осмыслить содержание задачи, поиску решения. При удачно составленной модели часто задачи, казалось бы, сложные для учащихся, решаются устно. В педагогической литературе и практике можно встретить следующие способы моделирования. 1) Предметная модель- описанная в задаче ситуация воспроизводится с помощью различных предметов (кубики, палочки и т.п.) или драматизацией, т.е. дети становятся участниками этой ситуации и показывают "небольшой спектакль" с предметами, описанными в задаче. Например, в задаче "У Саши было 6 книг, ему подарили еще 4 книги. Сколько книг стало у Саши?": а) вместо книг берут 6 палочек, кладут к ним еще 4 палочки и далее обсуждают решение; б) драматизация - к доске выходит Саша, берет 6 книг. Ему Наташа "дарит" еще 4 книги. Далее идет обсуждение. Предметная модель используется в начальном этапе обучения решению задач и в тех случаях, когда учащиеся не справляются с другими способами. В то же время, чрезмерное увлечение этим способом приводит к задержке развития детей. 2) Графическая модель- показ задачи с помощью графических изображений с использованием математических символов, фигур и т.п. 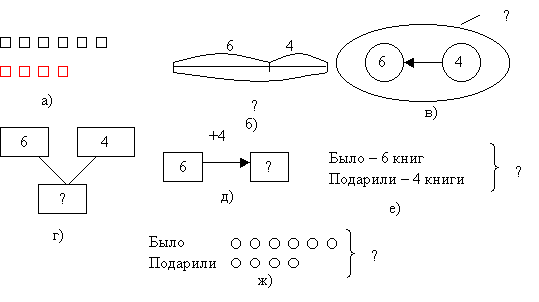 Вышеприведенная задача может иметь такие модели (рис. а, б, в, г, д). Такие модели достаточно конкретны, зрительно хорошо воспринимаются и достаточно отражают данные задачи и связи между ними. Моделирование задачи отрезками целесообразно использовать при решении задач, в которых даны отношения значений величин (больше, меньше, столько же), а также при решении задач на движение. В последнем случае отрезок изображает пройденное расстояние, стрелки – направление движения, флажком или другим знаком - "пункты" на пути движущегося тела. Значение скорости подписывают над стрелкой, время - над отрезком, длину пути - под соответствующим отрезком. При этом большее расстояние изображают большим отрезком. К задаче "Два пешехода вышли одновременно навстречу друг другу из двух сел и встретились через 3 часа. Первый пешеход шел со скоростью 4 км/ч, второй - 6 км/ч. Найди расстояние между селами" чертеж выглядит так: 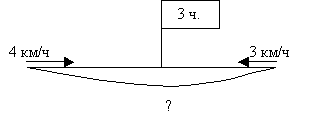 3) Словесно-графическая модель - это схематическая краткая запись текста задачи (е, ж). Такие модели, в основном, используются в задачах в 3-4 действия с целью запоминания условия задачи и выполняются они после ее восприятия и осмысления. При решении простых задач их применение нецелесообразно (кроме случаев показа новой формы записи), т.к. учащиеся больше тратят времени на записи (к которой они после не возвращаются), чем на решение задачи. 4) Табличная модель - запись условий и вопроса задачи в форме таблицы. З а д а ч а. Двое рабочих, работали одинаковое число дней. Один из них изготовлял в день 212 деталей, другой 218. Сколько деталей за это время изготовил второй рабочий, если первый изготовил 1060 деталей? Эту задачу можно кратко записать в таблице:
При табличной форме записи выделяются названия величин (число дней, дневная норма, число деталей). На одной строке записываются соответствующие значения различных величин, а значения одной величины - одно под другим. Искомое обозначается вопросительным знаком. В табличной форме записываются обычно составные задачи на нахождение четвертого пропорционального, на пропорциональное деление, на нахождение неизвестного по двум разностям. Работа учащихся с первых уроков со счетным материалом, кружками является подготовкой к обучению учащихся строить предметные модели задач. Целенаправленное обучение начинается после знакомства с задачей и приемом практического воспроизведения ее содержания. На уроках учитель может: а) предложить изобразить предметами то, что говорится в задаче и по ним выяснять условие и вопрос; б) выставить на наборном полотне кружки и предложить составить задачу (3 красных кружка изображают книги Тани, 4 зеленых - книги Саши. Составьте задачу.); в) на наборном полотне выставить предметные модели и попросить назвать ту, которая подходит к выбранной задаче; г) предложить решить задачу, предварительно самостоятельно построив ее модель. После усвоения моделирования предметами постепенно переходят к другим способам моделирования. На этапе моделирования задачи учитель должен оказывать сначала стимулирующую помощь (Как бы вы показали в задаче 4 книги?) В случае затруднения переходит на направляющую помощь (Нельзя ли 4 книги показать какими-либо кружками?) Если и в этом случае возникают затруднения, то использует обучающую помощь (Покажем 4 книги красными кружками). Постепенно учитель добивается необходимой самостоятельности учащихся. При обучении учащихся моделированию задачи необходимо научить их выбирать оптимальную модель. Это достигается систематической и целенаправленной работой. Конец формы 3. Поиск плана решения задачи Поиск плана решения фактически начинается на этапе моделирования. Здесь можно провести разбор задачи. Разбор задачи - это выявление зависимостей между данными величинами, между искомой величиной и данными, расчленение задачи на основе этих зависимостей на более простые и установление последовательности их решения для получения ответа на вопрос задачи (составление плана решения). При ознакомлении с новым видом простых задач учитель сам ведет разбор, учащиеся отвечают на вопросы. Например, при разборе задачи: "У Коли 8 марок, а у Шуры на 2 меньше. Сколько марок у Шуры?" - целесообразно поставить такие вопросы: Что требуется узнать в задаче? (Сколько марок у Шуры.) А их было больше или меньше, чем у Коли? (Меньше, потому, что сказано, что у Шуры марок на 2 меньше.) Если меньше, то каким действием решается задача? (Вычитанием.) Далее выполняется решение. Если же при разборе работаем по модели, то сначала рассуждения ведутся на "языке модели": "У Шуры кружков больше или меньше?", "Отрезок, показывающий марки Шуры, короче или длиннее?" и после этого снова повторяем со словом "марки". При ознакомлении с новым видом составных задач рассуждения ведутся аналогично. Здесь учащиеся накапливают опыт осуществления разбора по указаниям учителя. Разбор составной задачи заканчивается составлением плана решения. Учитель, переходя к специальному знакомству учащихся с разбором задачи, знакомит их с одним из видов рассуждений: от вопроса задачи к числовым данным или же от числовых данных к вопросу. Это может быть сделано без построения графических схем или же с построением. 1. Разбор задачи рассуждением от вопроса к числовым данным. Этот способ основан на анализе и в методической литературе часто называется "аналитический способ разбора задачи". При разборе задачи от вопроса к числовым данным рассматриваемый вопрос мысленно разбивается на другие вопросы, каждый из которых затем рассматривается в отдельности. В случае необходимости они, в свою очередь, разбиваются опять на другие вопросы и до тех пор, пока мы не придем к исходным данным задачи. З а д а ч а. Из двух городов А и В вышли навстречу друг другу одновременно два поезда. Один шел со скоростью 50 км/ч, другой - 60 км/ч. Какое расстояние между городами, если до встречи они шли 4 часа? Рассмотрим данный способ разбора, где рассуждения поэтапно изобразим в виде графической схемы (поэтапно изобразив рассуждения графически, получим схему на рис. 57). Что требуется узнать в задаче? (Расстояние между городами А и В.) Можно ли это узнать сразу? (Нет.) Что надо знать, чтобы найти расстояние от А до В? (Надо знать расстояние, пройденное каждым поездом до встречи.) Знаем ли расстояние, пройденное поездом из А? (Нет.) Что для этого надо знать? (Его скорость и время движения.) Знаем ли мы их? (Да, скорость 50 км/ч, время движения 4 ч.) Значит, сможем мы найти расстояние, пройденное поездом из А? (Да.) Известно ли расстояние, пройденное поездом из В? (Нет.) Что надо знать, чтобы его найти? (Скорость и время движения.) Знаем ли мы их? (Да, скорость 60 км/ч, время движения 4 ч.) Сможем ли мы теперь найти это расстояние? (Да.) Теперь составим план решения. Что мы найдем первым? (Расстояние, пройденное поездом из А.) Каким действием? (Умножим скорость на время.) Что найдем после этого? (Расстояние, пройденное поездом из В.) Каким действием? (Так же.) Что узнаем дальше? (Расстояние между городами.) Каким действием? (Сложением.) Ответим ли мы на вопрос задачи? (Да.) Рассуждение от вопроса к числовым данным представляет логическую цепь заключений, органически связанных между собой и поэтому оно хорошо развивает логическое мышление учащихся. Этот способ более целенаправлен на составление плана решения, т.к. ученик видит все рассуждение в целом. В системе развивающего обучения предпочтение отдается этому способу разбора задачи. 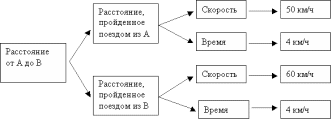 Рис. 57 2. Разбор задачи рассуждением от числовых данных к вопросу. Этот способ основан на синтезе и поэтому в методической литературе называют еще синтетическим методом разбора задачи. Рассмотрим разбор той же задачи данным способом (Поэтапно изобразив рассуждения графически, получим в конце схему на рис.58). Что нам известно в задаче о поезде из города А? (Его скорость 50 км/ч, время движения 4 ч.) Что мы можем найти по этим данным? (Расстояние, которое он прошел.) Каким действием? (Умножением.) О поезде из В что мы знаем? (Скорость 60 км/ч, время движения 4 ч.) Что можем найти по этим данным и каким действием? (Расстояние, умножением). Мы будем знать расстояние, пройденное каждым поездом до встречи. Что мы тогда сможем найти? (Расстояние между городами А и В.) Каким действием? (Сложением.) Ответим ли мы на вопрос задачи? (Да.) После этого аналогично составляется план решения задачи: 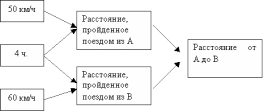 Рис. Этот способ разбора менее эффективен, т.к. он направлен на выбор действия, который может оказаться и ненужный. Например, используя 60 км/ч и 50 км/ч, ученик может выполнить вычитание: 60-50=10 (км/ч), которое в задаче совершенно не нужно. Графические схемы рассуждений представляют из себя схему самого процесса мысли, т.е. ученик наглядно видит движение мысли и результаты мыслительных операций. Обучению учащихся к построению таких схем следует начинать при введении составных задач в два действия. Постепенно у них развиваются навыки самостоятельного их составления. Конец формы § 4. Выполнение плана решения задачи Решение задачи - это выполнение арифметических действий, выбранных при составлении плана решения. Решение задачи может выполняться устно или письменно. При устном решении арифметические действия и пояснения выполняются устно. При письменном решении действия записываются, а пояснения к ним учащиеся либо записывают, либо проговаривают устно. В начальных классах наиболее распространенными являются следующие формы записи решения: З а д а ч а. В 6 вагонах поезда по 50 пассажиров, а в остальных 10 вагонах по 36 пассажиров. Сколько пассажиров в поезде? 1. Запись решения в виде выражения. а) Постепенная запись выражения с записью пояснения: 50·6 (пассажиров) - всего в 6 вагонах; 36·10 (пассажиров) - всего в 10 вагонах; 50·6+36·10=660 (пассажиров) - всего в поезде. Ответ: 660 пассажиров. б) Постепенная запись выражения без записи пояснений: 50·6 (пассажиров), 36·10 (пассажиров), 50·6+36·10=660 (пассажиров). Ответ: 660 пассажиров. в) Запись выражения без записи отдельных действий и пояснений: 50·6+36·10=660 (пассажиров). Ответ: 660 пассажиров. 2. Запись решения в виде отдельных действий. а) с записью пояснений: 1) 50·6=300 (пассажиров_ - всего в 6 вагонах; 2) 36·10=360 (пассажиров) - всего в 10 вагонах; 3) 300+360=660 (пассажиров) - всего в поезде. Ответ: 660 пассажиров. б) без записи пояснений: 1) 50·6=300 (пассажиров); 2) 36·10=360 (пассажиров); 3) 300+360=660 (пассажиров). Ответ: 660 пассажиров. 3. Запись вопросов и соответствующих действий. 1) Сколько пассажиров было в 6 вагонах? 50·6=300 (пассажиров). 2) Сколько пассажиров было в 10 вагонах? 36·10=360 (пассажиров). 3) Сколько пассажиров было в поезде? 300+360=660 (пассажиров). Ответ: 660 пассажиров 4. Запись каждого пункта плана с соответствующими действиями: 1) Найдем число пассажиров в 6 вагонах: 50·6=300 (пассажиров). 2) Найдем число пассажиров в 10 вагонах: 36·10=360 (пассажиров). 3) Найдем число пассажиров в поезде: 300+360=660 (пассажиров). Ответ: 660 пассажиров. В 1 классе достаточно научить детей записывать решение в виде выражения без записи пояснения, т.к. навыки письма у них слабо развиты. Начиная со 2-го класса можно переходить и к другим формам записи решения. Здесь при ознакомлении с задачами нового вида решение выполняется письменно и записывается под руководством учителя. При самостоятельной работе учитель рекомендует определенную форму записи. Решение задачи может быть записано в виде таблицы, геометрического чертежа, различных схем, рисунков, уравнений и др. Форму записи решения задачи выбирают исходя из конкретных целей. Если учитель сосредотачивает главное внимание на логической последовательности действий, то он выбирает оформление составлением выражения. Если же он хочет научить детей к сжатой и четкой математической речи, то целесообразно выбрать третий или четвертый способы. Грамотной записи при решении задач придается такое же значение, как и в упражнениях по русскому языку. В начальной школе в различных системах обучения изучается решение задач с помощью уравнений. В этом случае говорят о записи решения в виде уравнения Конец формы 5. Проверка решения задачи Проверить решение задачи - это значит установить, правильно она решена или неправильно. В начальных классах используются следующие способы проверки: 1. Прикидка ответа (установление соответствия искомого числа области своих значений). Применение этого способа состоит в том, что до решения задачи устанавливается область значении искомого числа, т.е. приблизительно в каких границах оно может быть по сравнению с данными задачи. Если после решения получают большие расхождения, значит задача решена неверно; если же эти расхождения незначительны - то, возможно, задача решена верно. З а д а ч а. В мешке было 45 кг моркови. 3 дня из мешка брали моркови поровну, после чего в нем осталось 33 кг. Сколько килограммов моркови брали из мешка каждый день? До решения выясняем: было 45 кг, осталось 33 кг. Значит, за три дня взяли меньше 33 кг, т.к. разность 45 и 33 меньше этого числа. Значит, в ответе число у нас должно быть меньше 33 кг. Решив задачу, в ответе получим 4 кг, которое меньше 33 кг. Наше решение, возможно, верное. Если бы мы получили 35 кг, значит, задача решена неверно. Надо проверить еще раз или другим способом. Прикидка чаще всего используется с другими видами проверки, которые дают однозначный ответ о правильности решения. Она вводится уже в 1 классе. 2. Установление соответствия между результатом решения и условием задачи. При проверке этим способом число, полученное в ответе, "подставляют" в задачу и выполняют действия. Если получатся числа, данные в условии задачи, то можно считать, что задача решена верно. З а д а ч а. В первых, вторых и третьих классах школы учатся всего 360 учащихся. В первых и вторых классах было 210 учащихся, во вторых и третьих классах -270 учащихся. Сколько учеников было в первых классах? во вторых классах? в третьих классах? Решив задачу, находим: в первых - 90, во вторых - 120 и в третьих 150 учащихся. Проверим условие задачи по полученным числам: во всех классах 90+120+150=360 (учащихся); в первых и вторых классах 90+120=210 (учащихся); во вторых и третьих классах 120+150=270 (учащихся). Полученные числа совпадают с данными, значит можно считать, что задача решена верно. Этот способ проверки используется, начиная со 2 класса. 3. Решение задачи другим способом. Если задачу можно решить различными способами, то получение одинаковых ответов подтверждает, что задача решена правильно. З а д а ч а. Из двух поселков, расстояние между которыми 260 км, выехали одновременно навстречу друг другу два мотоциклиста и встретились через 2 часа. Скорость одного из них 60 км/ч. С какой скоростью ехал другой мотоциклист?
При решении задачи разными способами получили одинаковые результаты, значит, задача решена правильно. Этот способ проверки вводится с 1 класса. 4. Составление и решение обратной задачи. В этом случае, после решения задачи, учащимся предлагают составить обратную задачу и решить ее. Если при решении обратной задачи в ответе получится число, которое было известно в данной задаче, то можно считать, что данная задача решена верно. З а д а ч а. В мешке было 50 кг крупы. Сначала оттуда взяли 12 кг, а потом 16 кг крупы. Сколько килограммов крупы осталось в мешке? Решив задачу 50-12-16=22 (кг), составим обратную задачу, для чего одно из данных задачи (50 кг) сделаем неизвестной, а 22 кг - известной. Получим задачу: "Из мешка сначала взяли 12 кг крупы, потом 16 кг и после чего осталось 22 кг. Сколько килограммов крупы было в мешке?" Решив эту задачу, получим в ответе 50 кг. Значит, первая задача решена правильно. Этот способ вводится со 2 класса. Проверка задач также может быть осуществлена сравнением с образцом решения какой-либо задачи этого типа, с некоторыми алгоритмами, теоретическими положениями и др. Проверке задач в обучении математике должно уделяться достаточное внимание хотя бы потому, что она воспитывает навыки самоконтроля, столь важные в жизни человека. Закрепление умений решать задачи На третьей ступени обучения решению задач ставится цель - закрепление умений решать задачи рассматриваемого вида. Учащиеся должны обобщить способ решения и научиться решать любую задачу данного вида. Обобщение способа решения не означает обучение запоминанию способа решения, при котором ученик узнав задачу знакомого вида, начинает вспоминать порядок действий. Усилия ученика должны быть направлены на раскрытие связей между данными и искомыми задачи и обоснованный выбор соответствующего действия. Для обобщения способов решения задач можно использовать различные методические приемы. 1. Повторение плана и решения задачи. Часто некоторые учащиеся, особенно со слабыми знаниями, при первичном решении задачи слабо вникают в ее смысл. Уделяя больше внимания вычислениям, они недостаточно вдумываются в связи между величинами, о которых говорится в задаче. Поэтому, после решения задачи целесообразно повторно кратко разобрать задачу, повторить план и решение задачи с объяснением. Это поможет им целиком осмыслить способ ее решения. При этом возможны различные варианты взаимодействия учителя и учащихся: 1) учащиеся закрывают тетради и отвечают на вопросы учителя; 2) записанное на доске решение частично учителем стирается и учащимися эта часть восстанавливается; 3) учитель повторение проводит с одним учеником, класс слушает; 4) повторение проводится с несколькими учащимися так, чтобы каждый ученик объяснил определенную часть задачи; 5) учитель меняет в условии некоторые числовые данные (вычисления должны быть сделаны устно), чтобы повторение не было простым воспроизведением и т.д. Такие приемы хорошо развивают восприятие, математическую речь, гибкость мышления. На уроках повторение можно использовать сразу после решения, после некоторого времени. Большую роль в развитии учащихся играет повторение ранее решенных задач. Чтобы не было простого механического запоминания и воспроизведения, основное внимание учителю нужно уделить осознанию учащимися зависимостей между данными и искомыми величинами, лучшему осмыслению способов решения задач, связь их с другими задачами и т.д. При повторении решения запоминание все же в некоторой степени происходит. Оно должно быть направлено на запоминание не просто понятий, способа решения, а, прежде всего, способа рассуждения, без чего в дальнейшем ученик затрудняется в решении задач данного типа. Например, решив задачу: "У Сережи было 8 марок, что на 3 марки больше, чем у Тани. Сколько марок у Тани?", ученик должен запомнить рассуждение: "у Сережи на 3 марки больше, чем у Тани, значит, у Тани на 3 марки меньше, чем у Сережи" (обратимость мышления). В противном случае в дальнейшем, ориентируясь на понятие "на ... больше", он будет решать задачу сложением. 2. Подбор системы задач. Для правильного обобщения способа решения задач определенного типа большое значение имеет подбор системы задач и их расположение. В этом плане задачу учителя облегчают авторы учебников и дидактических материалов. В случае, когда учитель сам подбирает систему задач, он должен соблюдать следующие требования: 1) задачи должны постепенно усложняться; 2) усложнение первоначально идет путем увеличения числа действий, а потом изменением связей между данными и искомыми. Например, задачу на нахождение суммы "У Коли было 6 книг, у Саши - 8 книг. Сколько книг было у ребят?" усложняем увеличением числа действий: "У Коли было 6 книг, у Саши - 8 книг, у Пети - 2 книги. Сколько было книг у ребят?" и т.д.; 3) количество решенных однотипных задач должно быть достаточным; 4) для предупреждения формального запоминания способа решения, задачи должны чередоваться с задачами другого типа. 3. Сравнение при решении задач. Применение сравнения при решении задач возможно в нескольких вариантах. 1) Сравнение условий задач до их решения и прогнозирование решения.В этом случае: а) можно сравнить задачи на одинаковое действие (скажем, оба на нахождение суммы), но с разными данными и сюжетом. Вторая задача сравнивается с первой, решенной задачей и высказывается предполагаемый способ решения, который затем проверяется. Здесь происходит рассуждение по аналогии; б) можно сравнивать задачи на противоположные действия и "прогнозировать неправильный способ" решения. Числовые данные и сюжет задачи могут быть как одинаковыми, так и разными. Например, после решения задачи "У Маши было 4 книги, а у Сережы на 2 книги больше. Сколько было книг у Сережы?" предлагаем вторую задачу "У Тани было 6 букетов цветов, что на 2 букета больше, чем у Нины. Сколько букетов было у Нины?" и просим: "Сравните эту задачу с первой и скажите, как бы ее решили?". Учащиеся отвечают: "Так же, сложением", т.е. прогнозируют неправильный способ решения. Ошибочность прогноза обнаруживается либо после выполнения краткой записи задачи, либо в ходе разбора. Такая форма работы развивает у учащихся обратимость и гибкость мышления, навыки предварительного самоконтроля. Надо отметить, что отсутствие в системе работы учителя упражнений на ошибочные прогнозы формирует у них устойчивое ложное мнение о том, что выбранный ими способ решения обязательно должен дать правильный результат. Происходит как бы навязывание задаче выбранного метода решения, хотя, фактически, метод должен выбираться исходя из самой задачи. В конечном итоге все это формирует ограниченное мышление. 2) Сравнение решений задач по ходу решения применяется при решении некоторой задачи после решения аналогичной, которая является как бы образцом. Каждое действие сопровождается рассуждениями типа: "В той задаче мы вторым действием умножили, здесь наверное тоже так же. Проверим" и т.д. Данный вариант сравнения формирует у учащихся навыки текущего самоконтроля и развивает гибкость мышления. 3) Сравнение всей работы по задаче проводится после решения нескольких задач. Например, после решения двух вышеприведенных задач (о книгах и букетах) можно провести такую беседу: "Чем отличаются эти задачи (одна - о книгах, другая о букетах). Чем они похожи? (В обоих сказано: "на 2 больше".) Каким действием решили первую задачу? (Сложением.) Почему? (Число книг у Саши увеличилось.) А вторую задачу? (Вычитанием.) Почему? (У Тани букетов на 2 больше, значит у Нины на 2 меньше. У нее - уменьшается.) Показывают ли это ответы задач? (Да. В первом - 6, больше 4 на 2; во втором 4, меньше 6 на 2, т.е. 6 больше 4 на 2.) Сделаем вместе вывод: если в задаче сказано "на больше", то задача может быть решена и сложением, и вычитанием". 4. Составление и преобразование задач. Упражнения по составлению и преобразованию задач очень эффективны для обобщения способа их решения и развивают гибкость мышления. В этом плане можно использовать такие упражнения: 1) Постановка вопроса к данному условию, изменение содержания или вопроса. Учащимся предлагается поставить различные вопросы к условию задачи: "На платье пошло 4 м ткани, а на кофту - на 1 м меньше". Ученики могут поставить такие: Сколько ткани пошло на кофту? Сколько ткани пошло на платье и кофту? На сколько больше ткани пошло на платье, чем на кофту? и другие. В учебниках начальной школы постановка вопроса к условию задачи применяется еще и с ограничениями: "Поставь вопрос так, чтобы задача решалась двумя действиями". Примером изменения содержания или вопроса могут быть задачи с меняющимся содержанием, на перестройку действия. Используя названные упражнения, учащиеся учатся обобщать знания о связях между данными и искомым. 2) Составление задачи по данному вопросу. Учащимся предлагают составить условие задачи, например, с вопросом: "Сколько километров прошел пешеход?". При подборе данных они определяют, что в условии может быть скорость и время, или же расстояние между несколькими пунктами и т.п. Во всех случаях должны подбирать реальные данные (скорость - не более 5 км/ч, расстояние - между пунктами - не более 20-30 км, но уже не 300 км!). Для составления задач нужно использовать справочные данные, приводимые в учебниках, дидактических материалах. Можно их взять и из газет, детских журналов и т.п. 3) Подбор числовых данных или их изменение. Данный прием развивает умение сопоставлять задачу с реальной ситуацией и подбирать данные с учетом реальных количественных отношений. Предложив задачу "В школьном саду ... яблонь, а груш на ... меньше. Сколько всего яблонь и груш в саду?" выясняет, что яблонь, с учетом территории школы, может быть примерно не более 20-30 (уж не 400, тогда не справимся с уборкой и реализацией урожая), груш на 1 меньше – тоже как-то нереально, нужно другое число и т.д. Определенный интерес представляют упражнения на изменение числовых данных задачи, при котором задача решалась бы аналогичным способом (например, нереальные задачи - гл.3,§ 3) или же другим способом. Например, в задаче "Вова нарисовал 9 домиков, а Лида - на 4 домика меньше. Сколько домиков нарисовала Лида?", которая решается вычитанием, заменив условие "на 4 домика меньше" условием "на 4 домика больше", получим задачу, решаемую сложением. 4) Составление задач по аналогии. Задачи, имеющие одинаковую математическую структуру, называются аналогичными. Составление таких задач помогает учащимся осознанию общих связей между данными и искомым при разных жизненных ситуациях. Они составляются после решения данной задачи в разных вариантах: а) с подбором других числовых данных; б) с другим сюжетом, в) с другими величинами. Например, после решения задачи с величинами цена, количество, стоимость можно предложить составить похожую задачу с величинами скорость, время, расстояние. 5) Составление задач по краткой записи условия. Составить задачу про учеников класса: Мальчиков - 18 чел., Девочек - на 4 чел. меньше. Сколько всего? 6) Составление задач по их иллюстрациям. Составить задачу по схеме (рис.59) и по чертежу (рис.60): 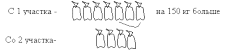 Рис. Сколько килограммов картофеля собрали с каждого участка?  Рис. Сколько километров прошел каждый пешеход до встречи? 7) Составление задач по решению (в виде выражения или отдельных действий). Составь задачи по выражениям: 1) 132·16-127·16 2) 300-(127+132+28) Дай ответ на вопрос каждой задачи. При выполнении таких заданий иногда полезно подсказать детям сюжет или же назвать величины. 8) Составление обратных задач. Составить задачу, обратную решенной (исходной) - это значит так преобразовать решенную задачу, чтобы полученный ответ стал данным, а одно из данных стал искомым. Обратных задач можно составить столько, сколько данных имеется в исходной задаче с одним данным. Рассмотрим з а д а ч у: "В поселке 210 каменных домов, а деревянных на 70 меньше. Сколько всего домов в поселке?" Обозначим высказывания: А: "210 каменных домов"; В: "деревянных домов на 70 меньше"; С: "всего домов в поселке". Наша задача имеет вид: А и В С. Составим обратные задачи: а) А и С В В поселке 210 каменных домов, а всего домов 350. На сколько деревянных домов меньше, чем каменных. б) С и В А В поселке 350 каменных и деревянных домов, причем деревянных на 7- меньше. Сколько в поселке каменных домов? в) С А и В В поселке всего 350 каменных и деревянных домов. Сколько всего каменных домов в поселке и на сколько деревянных меньше, чем каменных? Задачи вида а), б) называют просто обратными задачами, задачи вида в) - задачи с недостающими данными. Первоначальное ознакомление с методикой составления обратной задачи можно провести следующим образом. На уроке решается задача: "У Юры было 5 красных шаров и 3 синих. Сколько всего было шаров у Юры?". Краткая запись задачи изображается на наборном полотне (рис.61а): 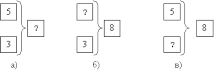 Рис. После решения данной задачи учитель меняет карточки как на рис.б и предлагает составить задачу. Решив эту задачу, составляют еще одну . Далее переходят к сравнению условия и замечают, что в последних двух случаях вопрос и одно данное задачи "поменялись местами". Учитель делает вывод о том, что задачи, в которых вопрос первой задачи стал одной из данных, а это данное стало вопросом, называют обратными задачами. В первоначальный период составления и решения обратных задач учащимся целесообразно работать с индивидуальными карточками как в данном случае. Для них очень важен сам механизм замены или, по-другому говоря, обратимость мышления мы демонстрируем им наглядно. В своей работе учитель должен чередовать разные приемы закрепления умения решать задачи рассматриваемого вида, а не отдавать предпочтение только некоторым из них. | |||||||||||||||
