Семестр 2. Задача и процесс ее решения. Вопросы и задания для подготовки к занятию

• Название: Задача и процесс ее решения. Вопросы и задания для подготовки к занятию
• Анкор: Семестр 2.doc
• Дата: 24.03.2018
• Размер: 289.5 Kb.
• Имя файла: Семестр 2.doc
• Тип: Задача; #17171
• страница: 3 из 7

Практическое занятие 2.4. Алгоритмы

Вопросы и задания для подготовки к занятию:

1. 
   Толкование понятия «алгоритм».
   
2. 
   Происхождение термина «алгоритм».
   
3. 
   Свойства алгоритмов.
   
4. 
   Способы записи алгоритмов.
   
5. 
   Виды алгоритмов.
   
6. 
   Установите, для решения каких задач используются следующие алгоритмы:
   

Алгоритм А.

1. 
   Пишу единицы под единицами, десятки под десятками, сотни под сотнями.
   

1. 
   Складываю единицы: 4 + 2 = 6.
   
2. 
   Складываю десятки: 6 + 4 = 10, десять десятков равны одной сот­не. Пишу под десятками 0, а одну сотню запомню и прибавлю к сотням.
   
3. 
   Складываю сотни: 2 + 5 = 7, да еще 1, получится 8. Пишу 8 под сотнями.
   
4. 
   Читаю ответ: 806.
   

Алгоритм Б.

1. 
   Отметь на листе бумаги точку О.
   
2. 
   Установи раствор циркуля равным длине отрезка АВ.
   
3. 
   Поставь ножку циркуля в точку О.
   
4. 
   Проведи окружность.
   

7. 
   Объясните, почему следующая программа действий является алгоритмическим предписанием:
   

Собери портфель

1. 
   Открой портфель.
   
2. 
   Положи в портфель тетради.
   
3. 
   Положи в портфель учебники.
   
4. 
   Положив портфель карандаш
   
5. 
   Положив портфель ручку.
   
6. 
   Закрой портфель.
   

8. 
   Составьте алгоритм построения отрезка длиной 5 см. Какие изменения произойдут в нем с изменением длины отрезка?
   

Задания для самостоятельной работы

1. 
   Является ли следующая программа действий алгоритмом или алгоритмическим предписанием:
   

А. Измерение длины отрезка АВ.

1. 
   Совместить линейку с отрезком АВ, совместив 0 с А.
   
2. 
   Отметить число, соответствующее точке В.
   
3. 
   Записать полученное значение.
   

Б. Построение биссектрисы угла.

1. 
   Провести циркулем дугу окружности, пересекающую стороны данного угла, и с центром в вершине угла.
   
2. 
   Обозначить точки пересечения дуги окружности со сторонами угла буквами А и В.
   
3. 
   Провести окружность с центром в точке А и тем же радиусом.
   
4. 
   Провести окружность с центром, в точке В и тем же радиусом.
   
5. 
   Обозначить одну из точек пересечения окружностей буквой С.
   
6. 
   Провести луч из вершины угла через точку С.
   

2. 
   Составьте алгоритм вычисления по формуле:
   
   1. 
      у = (5х-3) · (2х+7);
      
   2. 
      у = 2. (х +8) - 1.
      
3. 
   По приведенному алгоритму восстановите формулу для вычисления значения у:
   

1. 
   Умножить х на 4, обозначить ре­зультат R1.
   
2. 
   Сложить R1 с числом 7, обозна­чить результат R2.
   
3. 
   Разделить R2 на х, считать резуль­тат значением у.
   

2. 
   Составьте алгоритм вычислении в миллиметрах длины ломаной, состо­ящей из:
   
   1. 
      двух звеньев;
      
   2. 
      пяти звеньев
      
3. 
   Алгоритм решения неравенства х+2440 методом перебора задан при помощи блок схемы. Восстановите пропущенные шаги.
   

2. 
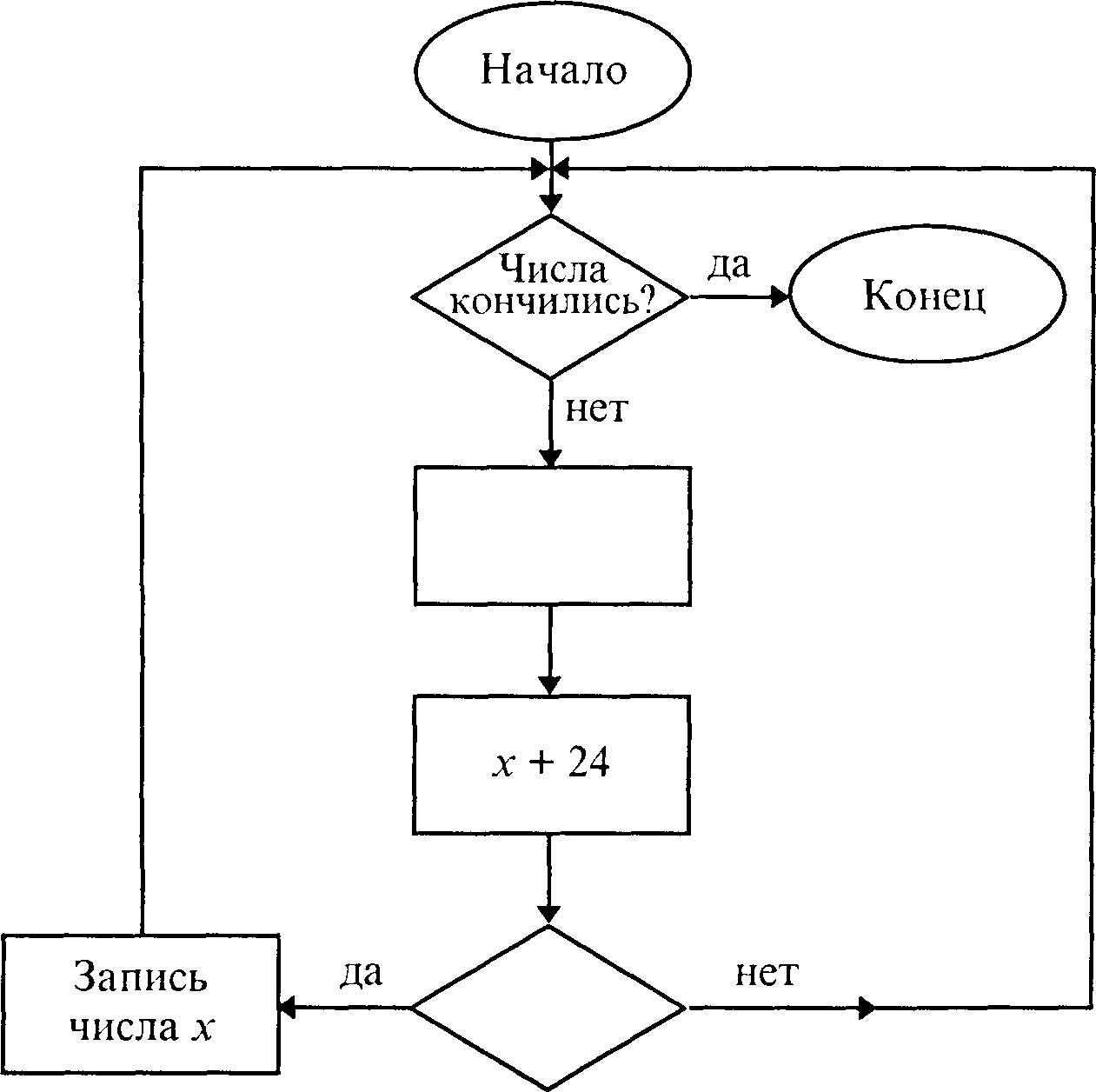
   Составьте и запишите алгоритм построения на клетчатой бумаге квад­рата со стороной 5 см. Какие изменения надо внести в него, чтобы построить квадрат: а) со стороной 5 см на нелинованной бумаге; б) со стороной любой длины?
   
3. 
   Используя прием пошаговой детализации, составьте алгоритм выполнения задания: «Определите логическую структуру и значение истинности высказывания, запишите его, используя символы». Про­верьте правильность составленного алгоритма для следующих выска­зываний:
   
   1. 
      28 кратно 4 и меньше 31;
      
   2. 
      28 кратно 4 или 9;
      
   3. 
      неверно, что 28 кратно 9.
      
4. 
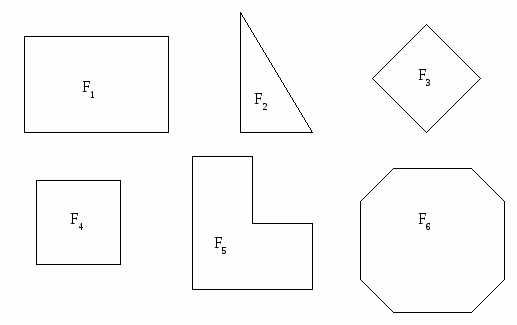
   Используя определение квадрата, составьте и запишите алго­ритм, позволяющий среди различных геометрических фигур распо­знавать квадраты. Применяя его, выполните задание: «среди следую­щих фигур выделите квадраты».
   

2. 
   Используя задание: «лежат ли три точки на одной прямой, если известны расстояния между ними: а) 3, 5, 8; б) 1, 4, 2; в) 6, 4, 5; г) 7, 11, 4; д) 3, 8, 12; е) 3, 6, 3?», разделите все случаи на группы в зависимости от результата; обобщите полученные выводы и постройте алгоритм принадлежности трех точек одной прямой. Каким приемом построения алгоритма вы воспользуетесь?
   

Примечание: расстояния между точками измерены с помощью одной и той же единицы длины.