Семестр 2. Задача и процесс ее решения. Вопросы и задания для подготовки к занятию
 Скачать 289.5 Kb. Скачать 289.5 Kb.
|
Практическое занятие 2.9. Числовые функции.Вопросы и задания для подготовки к занятию:
Задания для самостоятельной работы
а) б) в) 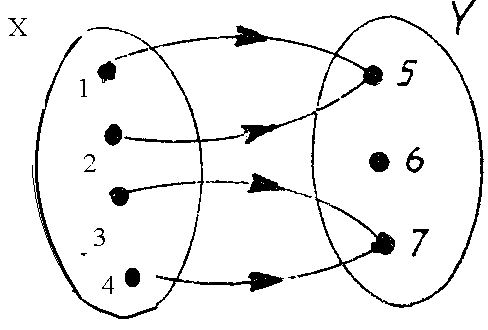 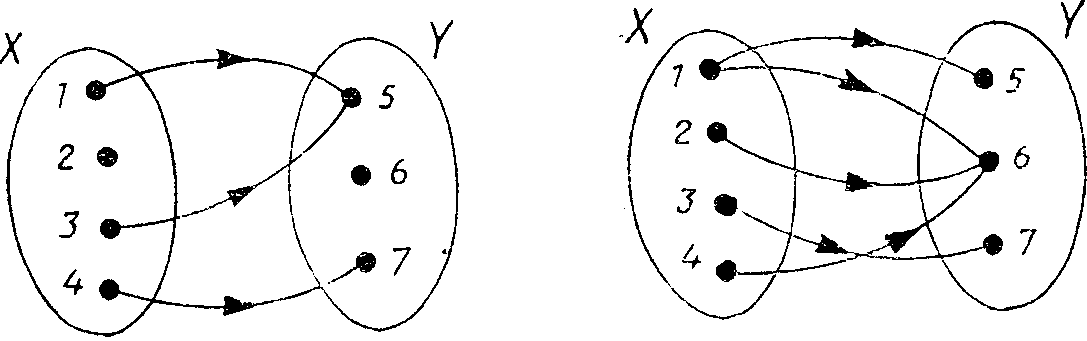 Рис.1 Рис.1
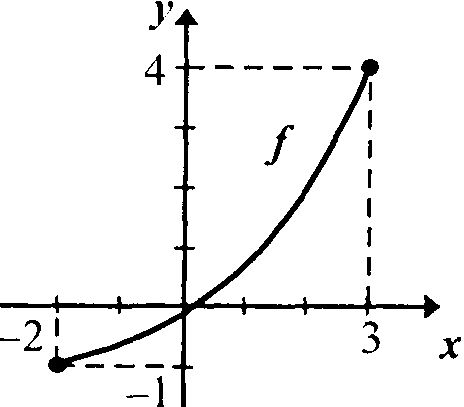 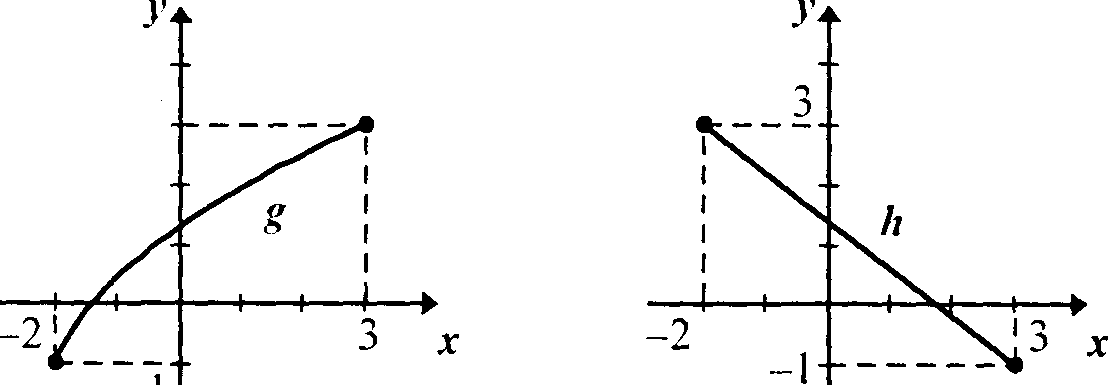 Рис. 2 Рис. 2
а) Х = {0, 1, 2, 3, 4, 5}; б) Х = [0; 5]; в) Х = R.
а) Укажите ее область определения и область значений. б) Задайте функцию f при помощи формулы. в) Постройте график функции f на координатной плоскости. д) Докажите, что функция f возрастает на всей области определении.
а) 39 + а. Вычисли сумму, если а принимает значения 0, 6, 15, 31, 46, 52. б) – 9. Вычисли разность, поставив в окошко числа 10, 11, 12. в) Составь все возможные примеры на сложение однозначных чисел с ответом 12. Покажите, что в каждом из этих заданий устанавливается соответствие между двумя числовыми множествами и это соответствие функция. Назовите в каждом случае область ее определения и область значений.
а) Катя купила 3 тетради, а Лена на х тетрадей больше. Сколько тетрадей (у) купили Лена и Катя вместе? б) Из пунктов А и В навстречу друг другу вышли два туриста. При встрече оказалось, что один прошел 3 км, а второй на х км больше. Каково расстояние (у км) между пунктами А и В?
а) Задайте функцию f при помощи формулы и таблицы; постройте ее график. б) Какие свойства функции f можно проиллюстрировать при помощи таблицы и графика? в) Какие из названных свойств вы будете использовать, решая задачу: «В 3 пакета разложили поровну 12 кг муки. Сколько килограммов муки можно разложить в 6 таких пакетов?»
а) Задайте функцию f при помощи формулы и таблицы; постройте ее график. б) Какие свойства функции f можно проиллюстрировать при помощи таблицы и графика? в) Какие из названных свойств вы будете использовать, решая задачу: «Муку разложили в 10 пакетов по 3 кг в каждый. Сколько получилось бы пакетов, если бы в каждый положили по 6 кг муки?»
Из 24 м ткани сшили 8 одинаковых платьев. Сколько потребуется ткани на 16 таких же платьев?
Задает ли эта таблица функцию? Какую? Какое свойство этой функции Можно проиллюстрировать при помощи данной таблицы?
а) Из каждых 10 м ситца получались 3 рубашки. Сколько таких рубашек можно сшить из 50 м ситца? б) Скорость машины 60 км/ч, скорость велосипедиста в 5 раз меньше. Велосипедист проехал расстояние от села до железнодорожной станции за 2 ч. 3а сколько минут можно проехать это расстояние на машине? в) За 15 м ткани уплатили 45 р. Сколько метров такой же ткани можно купить на 24 р.? г) Два столяра, один из которых работал 6 дней, а второй – 5 дней, отремонтировали по одинаковому количеству стульев. По сколько стульев в день ремонтировал второй столяр, если известно, что первый ремонтировал по 10 стульев в день? |
