Практическое занятие 2.1. Выражения, уравнения, неравенства.
Задания для самостоятельной работы
Среди следующих записей укажите числовые выражения:
а) 42:5; б) 27; в) 32+ -):14; г) 2·7 = 7·2;
д) (17+ 13):10-15; е) 142 > 71·2; ж) 37 – 48+3х
Какие из следующих выражений имеют смысл, если рассматривать их на множестве натуральных чисел:
а) (135+67)· 12; б) (135 - 217):2; в) 362:4?
Какие из нижеприведенных записей являются выражениями с переменными:
а) 8+0,3b; б) 21 - (4 + у); в) х + 2у < 7; г) 32:у + 3 = 5у?
Установите, какова область определения выражений, если рассматривать их на множестве действительных чисел:
а) (3 - у) : 64; 6) 64 :(3 - у); в) (5 + х) : (х - 12).
Известно, что выражение называется по своему последнему действию. Укажите порядок действий и дайте название каждому выражению:
Выражение
|
Название выражения
|
(12·5 + 3:(2+7))·18
|
|
(23 - 7·6 - 4+ 15)׃(17-6)
|
|
21 + (35·3:8 -14:5)
|
|
19 - 8:4 + 5
|
|
Выясните, являются ли выражения 3(4 - х) и 12 - 3х тождественно равными на множестве:
а) {1, 2, 3, 4}; б) действительных чисел.
Какие из следующих равенств являются тождествами на множестве действительных чисел:
а) 3р + 5m = 5m + 3р; в) 3р · 5m = 5m · 3р;
б) 3р – 5m = 5m - 3р; г) 3р:5m = 5m:3р?
Обоснуйте каждый шаг в преобразованиях следующих выражений:
а) 324·5 = (300+20+4) · 5 = 300· 5+20·5+4·5 = 500+100+20 = 1500+ 120 = 1620;
б) 97·12 = (100 - 3) · 12 = 100 ·12 - 3·12 = 1200 - 36 = 1100+(100 - 36) =1164;
в) 5(1-2х)+10х = 5 - 10х+10х = 5.
Упростите выражение путем тождественных преобразований:
а) 6(2аb - 3) + 2а (6b - 5); б) (12а - 16b):4 - (10а - 4b).
Сравните значения выражений, не выполняя действий:
а) (30 + 56) ·5 и 30·5 + 56·5;
б)(19 + 4) ·7 и 19·7 + 10·7;
в) (14 - 7) ·6 и 16·6 - 7·6;
г) (18 - 9) ·7 и 18·7 - 11·7.
Решите задачу; решение запишите в виде выражения:
На туристическую базу прибыли в один день 150 туристов, на другой день 170. Чтобы пойти по маршрутам, 200 туристов разбились на группы, по 20 человек в каждой, а остальные по 15 человек в группе. Сколько получилось групп?
Среди следующих записей найдите числовые равенства и неравенства:
а) 3х + 4=57:3; б) 34 - 48:12=(7 + 8) ·9; в) 39·3 + 74 - 53; г) 37 < 18; д) 3х + 4< 71; е) 65 > 344 + 148:74
Проверьте, истинны ли числовые равенства:
13 · 93 = 31·39, 14·82 = 41·28, 23·64 = 32·46.
Можно ли утверждать, что произведение любых двух натуральных чисел не изменится, если в каждом множителе переставить цифры?
Известно, что х > у - истинное неравенство. Будут ли истинными следующие неравенства:
а) 2х > 2у; в) 2х - 7 < 2у - 7;
б) 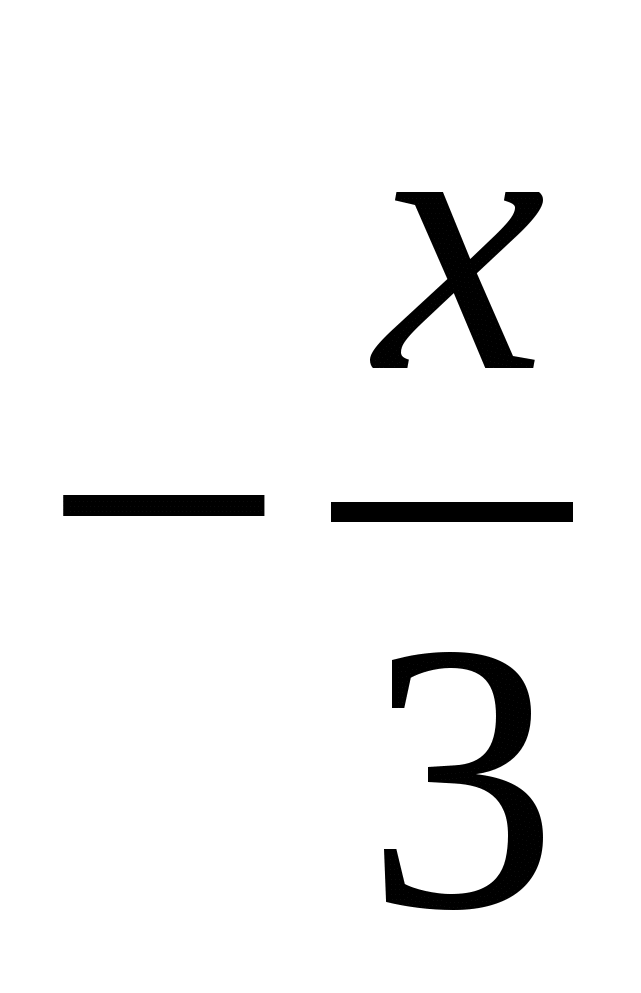 < -3 ; г) - 2х - 7 < - 2у - 7? < -3 ; г) - 2х - 7 < - 2у - 7?
Известно, что а < b — истинное неравенство. Поставьте вместо * знак «>» или «<» так, чтобы получилось истинное неравенство:
а) -3,7а * -3,7b; б) - 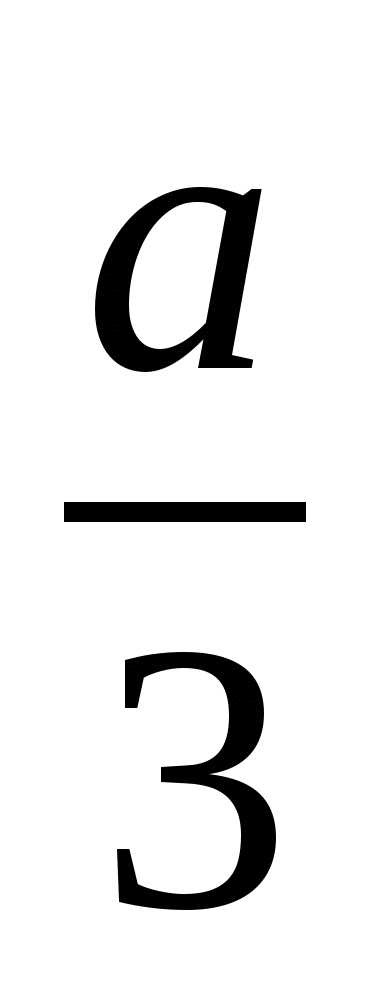 * - * - 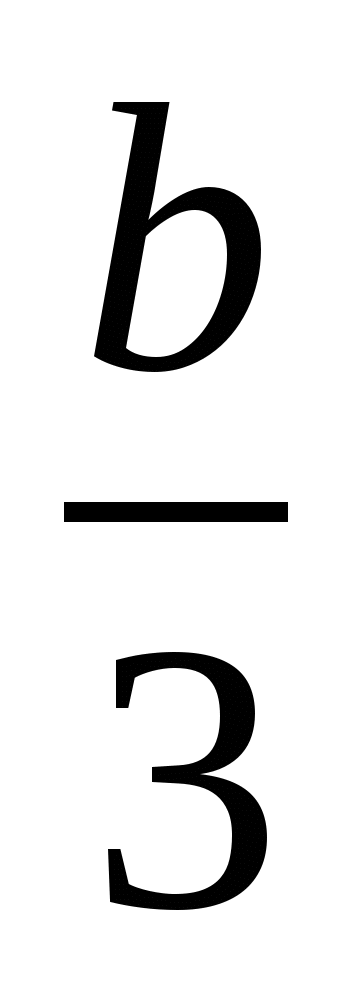 ; в) 0,12а * 0,12b; ; в) 0,12а * 0,12b;
г) -2(а + 5) * -2(b + 5); д) 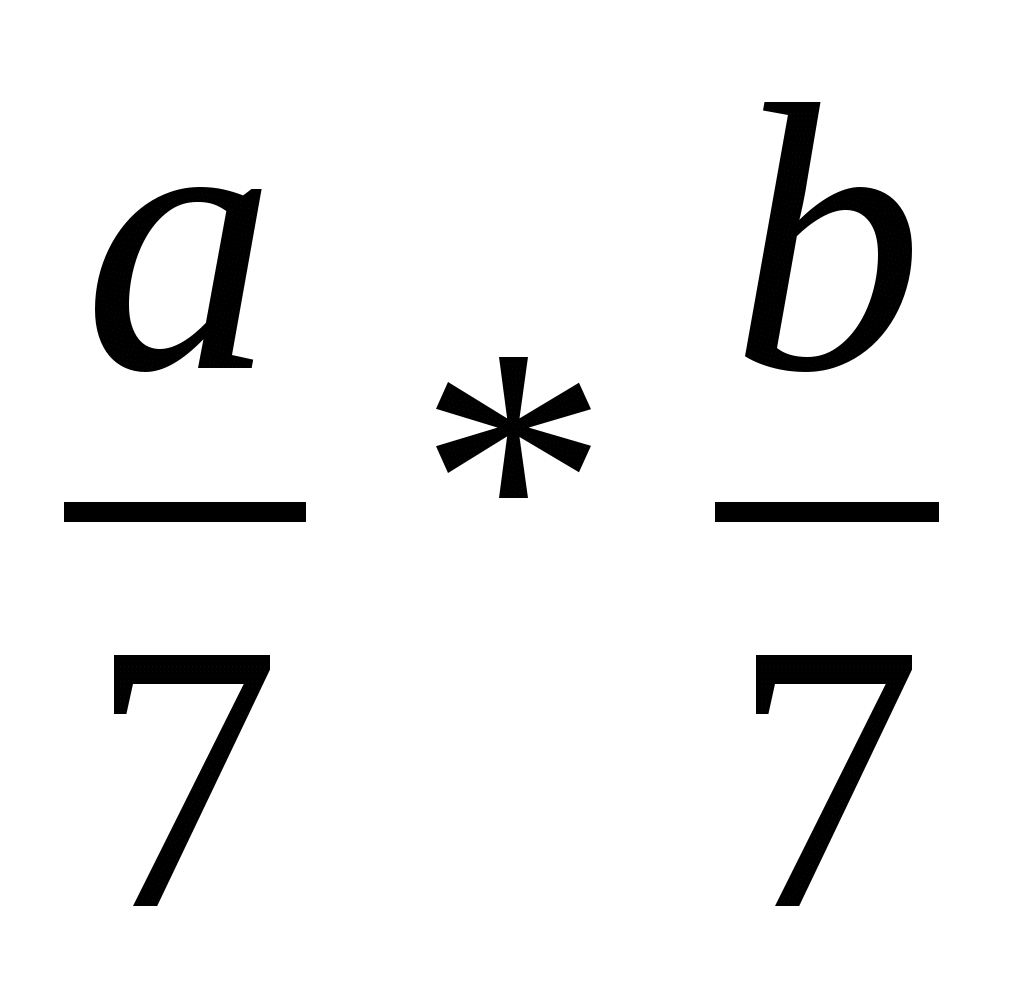 ; е) ; е) 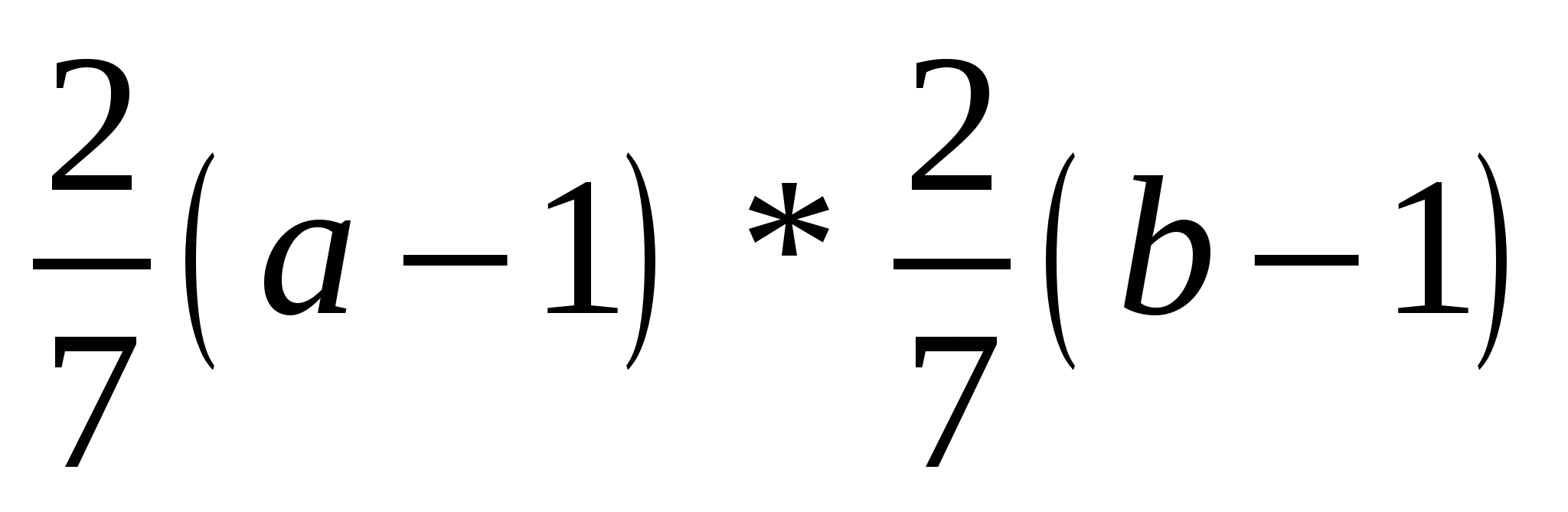
Выполните задания, которые предназначаются ученикам начальных классов, и сделайте вывод о том, как трактуются в начальном курсе математики понятия числового равенства и числового неравенства:
а) Запиши два верных равенства и два верных неравенства, используя выражения: 9 ·3, 30 - 6, 3·9, 30 - 3.
б) Расставь скобки так, чтобы равенства были верными: 4 + 2 ·3 = 18; 31- 10 – 3 = 24; 54 – 12 + 8 = 34.
в) Поставь вместо * знаки действий так, чтобы получились верные равенства: 3 * 6 * 2 = 9; 9 * 3 * 6 = 18.
Установите, какие из следующих записей являются уравнениями с одной переменной:
а) (х - 3)·5 = 12х; г) 3 + (12 - 7) ·5 = 16;
б) (х - 3)·5 = 12; д) (х - 3)·у = 12х;
в) (х - 3) - 17 + 12; е) х2 - 2х + 5 = 0.
Уравнение 2х4 + 4х2 - 6 = 0 задано на множестве натуральных чисел. Объясните, почему число 1 является корнем этого уравнения, а 2 и -1 не являются его корнями.
В уравнении (х + ...)(2х + 5) - (х - 3)(2х + 1) = 20 одно число стерто и заменено точками. Найдите стертое число, если известно, что корнем этого уравнения является число 2.
Сформулируйте условия, при которых:
а) число 5 является корнем уравнения f(х) = g (х);
б) число 7 не является корнем уравнения f(х) = g (х).
Установите, какие из следующих пар уравнений равносильны на множестве действительных чисел:
а) 3 + 7х = - 4 и 2(3 + 7х) = -8;
б) 3 + 7х = - 4 и 6 + 7x = -1;
в) 3 + 7х = - 4 и х + 2 = 0.
Решите уравнения (все они заданы на множестве действительных чисел) и обоснуйте все преобразования, выполняемые в процессе их упрощения:
а)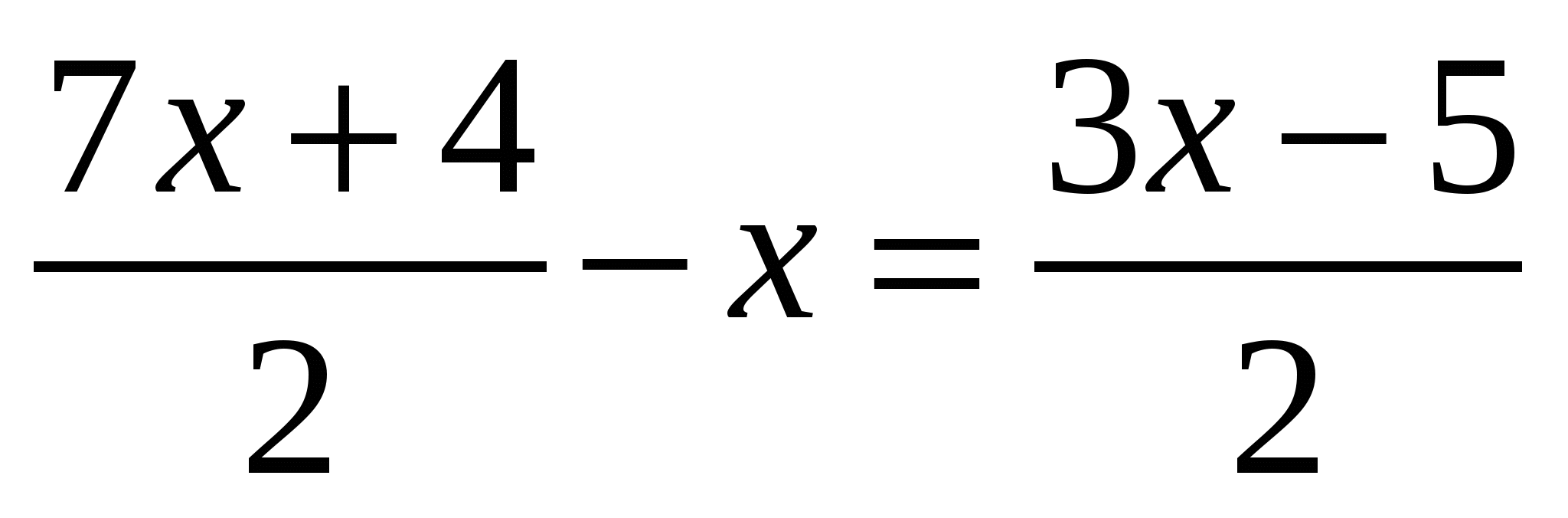 ; б) ; б) 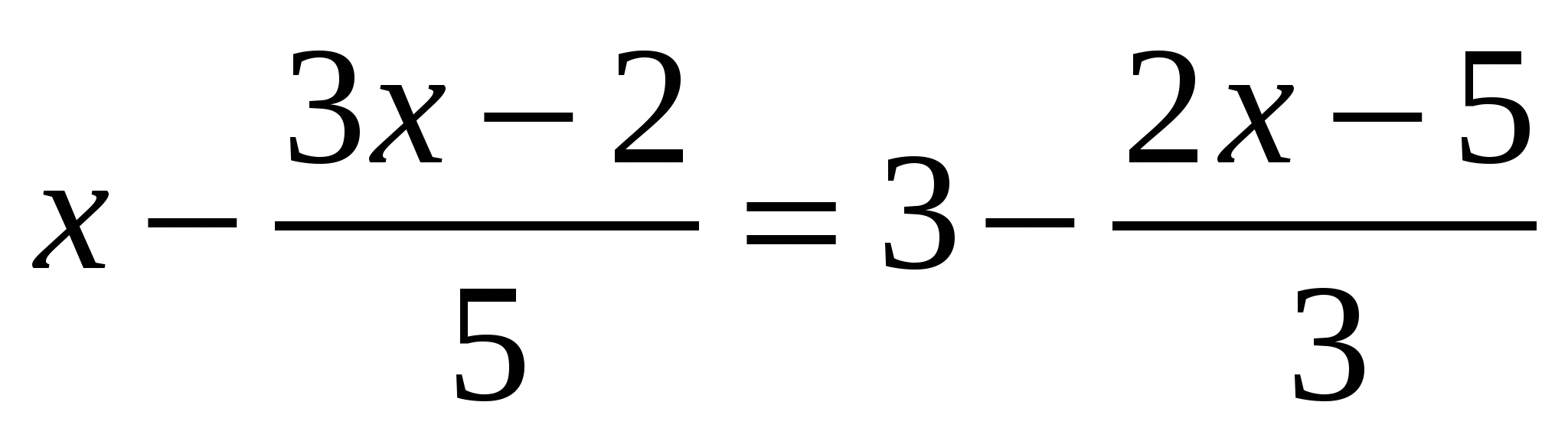
в) (2 - х)2 - х(х + 1,5) = 4.
Учащийся решил уравнение 5х + 15 = 3х + 9 следующим образом: вынес за скобки в левой части число 5, а в правой число 3, получил уравнение 5(х + 3) = 3(х + 3), а затем разделил обе части на выражение х + 3. Получил равенство 5 = 3 и сделал вывод - данное уравнение корней не имеет. Прав ли учащийся?
Решите уравнения, используя взаимосвязь между компонентами и результатами действий:
а) (х + 70) · 4 = 328; в) (85х + 765) :170 = 98;
б) 560: (х + 9) = 56; г) (х -13581):709 = 306.
Решите задачи арифметическим и алгебраическим способами:
а) На первой полке на 16 книг больше, чем на второй. Если с каждой полки снять по 3 книги, то на первой полке книг будет в полтора раза больше, чем на второй. Сколько книг на каждой полке?
б) Весь путь от турбазы до станции, равный 26 км, велосипедист проехал за 1 ч 10 мин. Первые 40 мин этого времени он ехал с одной скоростью, а остальное время - со скоростью на 3 км/ч меньше. Найдите скорость велосипедиста на первом участке пути.
Установите, какие из следующих записей являются неравенствами с одной переменной:
а) -12 - 7 х < 3х + 8; г) 12 х + 3(х - 2);
б) 15 (х + 2) > 4; д) 17 - 12·8;
в) 17 (13 + 8) < 14 - 9; е) 2х2 + 3х - 4 > 0.
Является ли число 3 решением неравенства 6(2х + 7) < 15(х + 2), х R? А число 4,25?
Равносильны ли на множестве действительных чисел следующие пары неравенств:
а) -17х < -51 и х > 3;
б)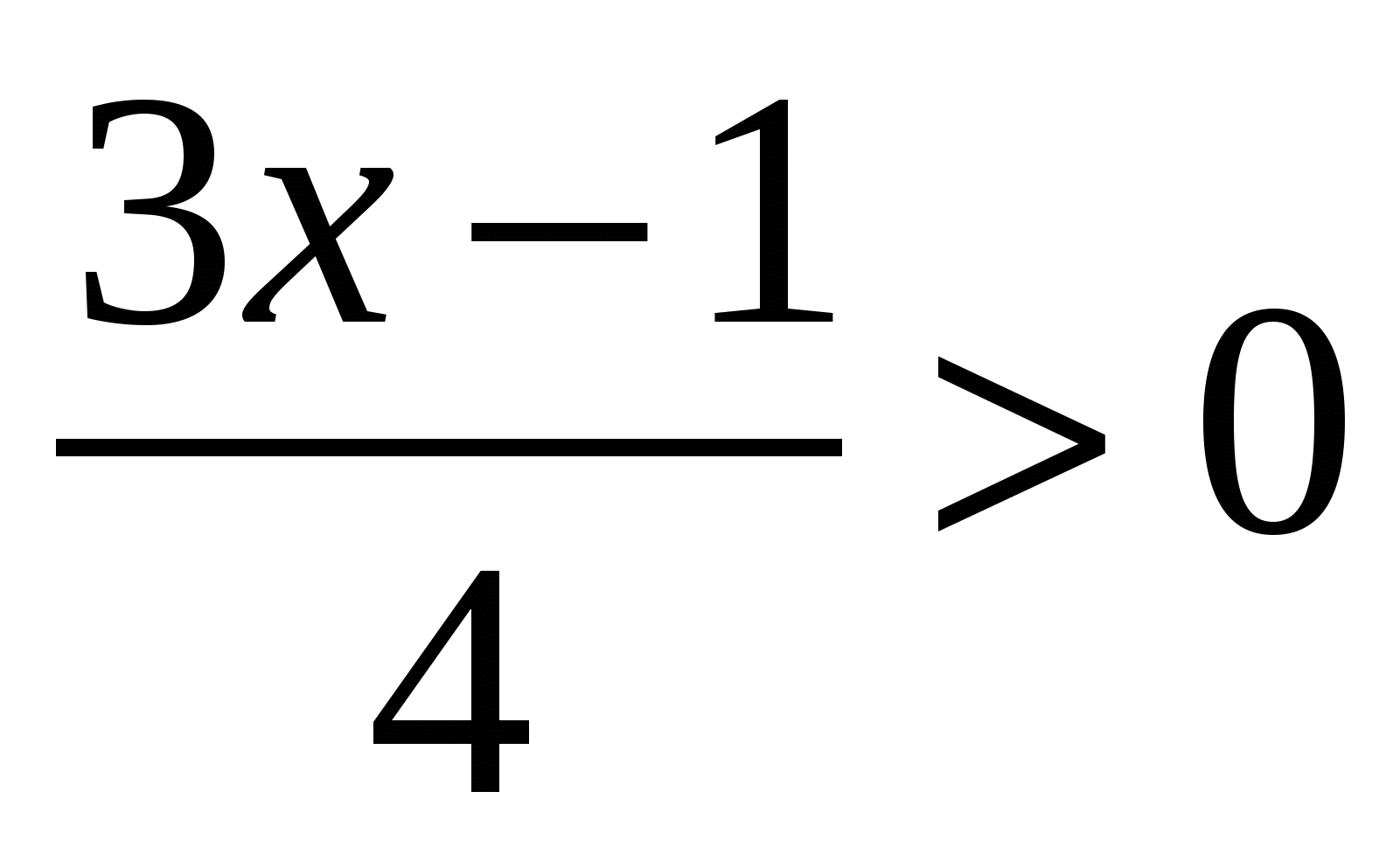 и 3х - 1 > 0 и 3х - 1 > 0
в) 6 - 5х > -4 и х < 2?
Какие из следующих высказываний истинны:
а) -7 х < -28 х > 4;
б) х < 6 х < 5;
в) х < 6 х < 20?
Решите неравенство 3(х - 2) - 4(х + 1) < 2(х - 3) - 2 и обоснуйте все преобразования, которые будете при этом выполнять.
Докажите, что решением неравенства 2(х + 1) + 5 > 3 - (1 - 2х) является любое действительное число.
Докажите, что не существует действительного числа, которое являлось бы решением неравенства 3 (2 - х) - 2 > 5 - 3х .
Практическое занятие 2.12. Алгебраические операции.
Вопросы и задания для подготовки к занятию:
Алгебраическая операция.
Свойства операций.
Нейтральный и поглощающие элементы.
Обратная операция и симметричный элемент.
Алгебра (Z0; +; ).
Сформулируйте условия, при которых операция, заданная на множестве Х:
а) будет алгебраической; б) Не будет алгебраической.
Объясните, почему сложение и умножение являются алгебраическими операциями на множестве Z целых чисел, а деление не является.
На множестве Х = {-1, 0, 1} заданы сложение, умножение и вычитание. Являются ли они алгебраическими на этом множестве?
Являются ли алгебраическими операции: сложение, умножение, деление и вычитание, заданные на множестве Х, если:
а) Х – множество четных натуральных чисел;
б) Х– множество нечетных натуральных чисел;
в) Х– множество натуральных чисел, кратных 5?
Среди следующих высказываний укажите истинные, ответ обоснуйте:
а) Множество N натуральных чисел замкнуто относительно умножения.
б) Множество Q рациональных чисел замкнуто относительно деления (деление на нуль не рассматривается).
в) Множество Z целых чисел замкнуто относительно вычитания и деления.
г) Множество Z целых чисел замкнуто относительно вычитания или деления.
Являются ли алгебраическими на множестве натуральных чисел следующие операции:
а) возведение в степень;
б) нахождение наибольшего общего делителя двух чисел;
в) нахождение наименьшего общего кратного двух чисел?
Дано множество {а, b, с}. Составьте множество Х всех его подмножеств. На этом множестве Х рассмотрите операции пересечения и объединения. Являются ли они алгебраическими?
Какие из следующих алгебраических операций в множестве целых чисел Z, являются коммутативными: а) сложение; б) вычитание; в) умножение; г) операция, задаваемая формулой (х, у) →2х - у; д) операция, задаваемая формулой (х, у)→ х2 - у2
Обладает ли свойством коммутативности: а) операция объединения множеств; б) операция вычитания множеств; в) операция пересечения множеств?
Какие из следующих алгебраических операций в множестве Q рациональных чисел являются коммутативными: а) сложение; б) умножение; в) вычитание; г) операция, задаваемая формулой (х, у) → х + 2у; д) операция, задаваемая формулой (х, у) →х2 + у2 ?
Какие из следующих операций в множестве Z целых чисел ассоциативны: а) сложение; б) вычитание; в) умножение; г) операция (х, у) →х + 2у; д) операция (х, у) →х2 + у2?
Являются ли пересечение и объединение множеств ассоциативными операциями?
Является ли ассоциативной операция возведения в степень в множестве натуральных чисел? Проверьте, выполняется ли, например, равенство 2 * (1 * 3)= (2 * 1) * 3, где т* п = тп.
Какое число является нейтральным относительно операции сложения целых чисел? Есть ли нейтральный элемент для сложения натуральных чисел?
Какое число является нейтральным относительно операции умножения целых чисел?
Найдите нейтральный элемент для операции (х, у)→х + у + ху в множестве рациональных чисел.
Какое множество является нейтральным элементом относительно операции объединения множеств? Существует ли нейтральный элемент для операции пересечения множеств (рассматриваются лишь подмножества универсального множества U).
Является ли деление в множестве положительных чисел дистрибутивным относительно операции сложения?
Является ли операция объединения множеств дистрибутивной относительно операции пересечения множеств? Ответ поясните с помощью диаграмм Эйлера—Венна.
Сократимо ли вычитание и деление на множестве Q?
Какое множество является поглощающим элементом относительно операции пересечения множеств?
|
 Скачать 289.5 Kb.
Скачать 289.5 Kb.