Ответы Техмех. Задача механики деформируемого твердого тела исследование напряженного и деформированного состояний твердых тел при различных воздействиях
 Скачать 3.28 Mb. Скачать 3.28 Mb.
|
|
Экзаменационные вопросы по ТМ 1.Задачи технической механики. Основная задача механики деформируемого твердого тела – исследование напряженного и деформированного состояний твердых тел при различных воздействиях. 2.Основные понятия, гипотезы и принципы. Понятия о расчетных схемах. Виды нагрузок. Напряжения – внутренние силы, отнесенные к единице площади, возникающие при действии нагрузок в твердых телах, характеризующие сопротивление тела деформации. Прочность – способность безопасной работы конструкции, сооружения или отдельных элементов, к-ая исключала бы возможность их разрушения. Устойчивость конструкции – ее способность сохранять вплоть до разрушения первоначальную форму равновесия. Жесткость конструкции х-т ее способность препятствовать развитию деформаций. Деформация – изменение формы и размеров тела под действием нагрузки. Процесс деформирования называется абсолютно упругим, если после снятия нагрузки деформации полностью исчезают и при этом восстанавливаются первоначальные размеры тела и его форма. Такой процесс соответствует гипотезе об абсолютной или идеальной упругости тела. Часть суммарной деформации, исчезающей после снятия нагрузки, называется упругой. Деформация, остающаяся после разгрузки, называется остаточной или пластической. В общем случае при достаточно больших нагрузках материалы проявляют упругие и пластические св-ва. Материалы – упругопластические. Допущения о свойствах материала: Изотропность – механические св-ва во всех направлениях одинаковы Сплошность – не учитывается конкретная структура материала(зернистая, кристаллическая и пр) и считается, что материал заполняет непрерывно весь объем элемента конструкции. Однородность – весь объем материала обладает одинаковыми механическими св-ми Линейно-упругость Принцип независимости действия сил: какой-либо результат действия нагрузки можно представить как сумму аналогичных результатов действия по отдельности всех составляющих нагрузки Принцип Сен-Венана: напряженное состояние тела на достаточном удалении от области действия локальных нагрузок очень мало зависит от детального способа приложения этих нагрузок/ принцип локальности эффекта действи взаимно уравновешенных нагрузок в малой области. К числу основных типов элементов, на которые в расчетной схеме подразделяется целая конструкция, относ стержень или брус, пластина, оболочка, массивное тело. Схематизация и упрощения, касающиеся х-ра действия нагрузок, усл опирания и тд. Отражает наиб существенное для х-ра работы данной конструкции Расчетная схема есть упрощенное представление сооружения, учитывающее основные данные, определяющие поведение объекта под нагрузкой. Виды нагрузок: поверхностные и объемные, активные нагрузки и реакции связей, распределенные и сосредоточенные, статические и динамические, постоянные и временные. 3.Напряжения и внутренние усилия в поперечном сечении стержня. Нормальные напряжения Касательные напряжения Две поперечных силы – Qy Qz Продольная сила – N Два изгибающих момента – Mz My Крутящий момент - Мх 4.Геометрические характеристики поперечных сечений стержней. Статический момент инерции, осевые моменты инерции, центробежный момент инерции, полярный момент инерции, площадь, радиус инерции , момент сопротивления. 5.Статические моменты и моменты инерции. 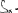 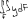  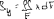  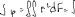     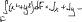 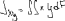  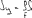 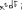 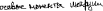 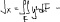 6. Зависимости между моментами инерции относительно параллельных осей. 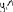  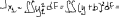 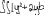 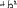 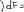 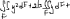 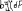  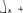 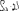     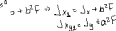 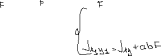    7.Изменение моментов инерции при повороте координатных осей. 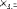  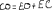    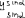 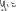 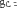 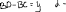  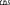 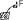   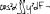    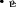         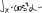 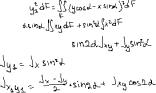  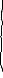           8.Главные осы и главные моменты инерции. Две взаимно перпендикулярные оси, относительно к-х центробежный момент инерции равен нулю. Осевые моменты инерции относ таких осей имеют экстремальные значения – один Jmax, другой Jmin – главные моменты инерции. Если главные оси проходят через центр тяжести сечения – главные центральные оси  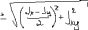  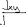 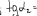  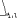 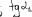 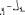 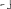  9.Моменты инерции простых сечений, моменты инерции составных сечений.  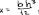 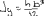   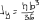 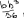    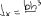 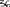  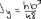 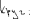 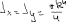 10.Центральное растяжение и сжатие стержня. Определение продольных сил. Центральное(осевое) растяжение и сжатие стержня – вид деформирования, при котором все внешние нагрузки или их равнодействующие действуют вдоль оси стержня(осевые нагрузки) При нагружении стержня осевыми нагрузками в его поперечных сечениях возникают только продольные(нормальные силы). Метод определения – метод сечений. Продольная сила в сечении, связанная с деформацией растяжения или сжатия. 11.Деформации и напряжения при центральном растяжении и сжатии стержня. Продольная сила явл интегральной х-ой, к-ая связана с нормальными напряжениями, действующих в сечении Гипотеза плоских сечений Я.Бернулли: сечения, плоские и перпендикулярные к оси стержня до деформации, остаются плоскими и перпендикулярными к оси после деформации. При растяжении м сжатии длина всех продольных волокон стержня изменяется на одинаковую величину. Нормальные напряжения распределены по сечению равномерно. N=ơF; ơ=N/F При растяжении и сжатии стержня изменяется его длина и размеры поперечного сечения. Абсолютное удлинение: du=d(∆x)=dx1-dx ; 𝜀 = d(∆x)/dx = du/dx – относительная линейная деформация; 𝜀’ = -∆b/b – поперечная деформация 𝝂 = |𝜀’/𝜀| - коэффициент Пуассона, характеризующий способность материала к поперечным деформациям(0;0,5); Ơ = E𝜀 – закон Гука; Е – модуль упругости, характеризует жесткость материала; 12.Определение осевых перемещений. du=d(∆x) = 𝜀dx – интегрируя от 0 до х – u(х)=∆x= ∫𝜀dx + C, где С = u(0) – осевое перемещение начального сечения х = 0, если сечение закреплено u(0) = 0, u(x) – Осевое перемещение произвольного сечения. 13.Статически неопределимые задачи при центральном растяжении и сжатии. Задача статически неопределима, если из уравнений равновесия нельзя определить опорные реакции и внутренние усилия в стержне. В общем случае система является n раз статически неопределимой, если число неизвестных на n превышает независимых уравнений равновесия. Решается с трех сторон: 1) геометрическую 2)физическую 3) статическую . 14.Диаграммы растяжения и сжатия. Механические свойства материалов. 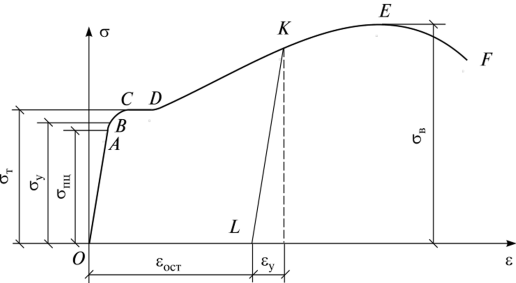 С С таль Диаграма Прандаля таль Диаграма Прандаля            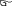  Наибольшее напряжение, до которого материал следует закону Гука – предел пропорциональности Наибольшее напряжение, при к-м в материале при разгрузке не возникают остаточные деформации – предел упругости Горизонтальный участок на диаграмме – площадка текучести, а напряжение -предел текучести. В малоуглеродистых сталях при напряжениях, равных пределу текучести, развиваются пластические деформации, связанные с необратимыми деформациями сдвига между кристаллами феррита. После развития опр пластических деформаций и перестройки кристаллической решетки стали несущая способность стержня увеличивается – рост деформации сопровождается увеличением напряжений, происходит упрочнение стали. DE – зона упрочнения. При напряжении, соотв наивысшей т-ке Е, в опру ч-ке образца появл заметное уменьшение размеров поперечного сечения - шейка. Отношение наибольшей силы, к-ую может выдержать образец, к первоначальной площади поперечного сечения - временное сопротивление(предел прочности). Диаграмма 1 для чугуна характерна тем, что практически до разрушения зависимость между 𝜀 и ơ явл линейной – хрупкие материалы. Диаграмма 2 для меди соотв пластичным материалам, у к-х отсутствует площадка текучести. Для таких материалов принимается условный предел текучести, при к-м остаточные деформации составляют 0.2%. 15. ?Методы расчета на прочность. Расчеты на прочность при центральном растяжении и сжатии. Расчет на прочность сводится к требованию, чтобы наибольшее напряжение в элементе конструкции(нормальные, касательные, либо комбинация этих напряжений) не превосходили некоторой допустимой для данного материала величины. Методы: Метод допускаемых напряжений; Метод предельных состояний; Метод разрушающих нагрузок; Метод предельных состояний: Предельное состояние – состояние конструкции, при к-м невозможно ее дальнейшая нормальная эксплуатация. Первая группа предельных состояний: определяется потерей несущей способности – прочности или устойчивости Вторая гр.пр.сост.: опр возникновением чрезмерно больших деформаций или колебаний сооружения; Третья гр.пр.сост: опр образованием и развитием трещин и др повреждений Условия прочности при расчете по первой гр.пр.сост сводятся к требованию, чтобы наибольшие растягивающие напряжения и наибольшие по абсолютной величине сжимающие напряжения от расчетных значений нагрузок не превышали величин расчетных сопротивлений при растяжении и сжатии умноженных на коэффициент условий работы       16.Напряженно-деформированное состояние в окрестности точки тела и его виды. Если через произвольную точку тела провести три взаимно перпендикулярные площадки параллельно координатным плоскостям, то 9 составляющих(компонент) напряжения: 3 ơx,ơy,ơz,txy ,tyz ,tzx ,tyx ,txz ,tzy , действующих на этих площадках, полностью определяют напряженное состояние в окрестности данной точки, зная эти 9 величин, можно найти напряжения на любой наклонной площадке, проходящей через данную точку. Индекс у нормального – параллельно какой плоскости оно действует, у касательного первый индекс – параллельно какой оси, а второй – нормаль к площадке, на к-й оно действует. Закон парности касательных напряжений: касательные напряжения, действующие на 2-х взаимно перпендикулярных площадках, направленные перпендикулярно к линии пересечения этих площадок, равны по величине. Трехосное состояние – сост, при к-м все 3 главных напряжения ơ1, ơ2, ơ3 отличны от нуля; Двухосное состояние – сост, при к-м одно из главных напряжений равно нулю; Одноосное состояние – сост, при к-м только одно из главных напряжений отлично от нуля. 17.Дифференциальные уравнения равновесия.     18.Главные площадки и главные напряжения. Напряжения на наклонных площадках. Двухосное напряженное состояние. Главные площадки – площадки, на к-х касательные напряжения отсутствуют, а напряжения действующие на них – главные напряжения; 19.Кручение стержней. Внутренние усилия при кручении. Напряжения в стержне круглого поперечного сечения при кручении. Анализ напряженного состояния. Главные напряжения. Кручение стержней вызывается действием нагрузок, дающих моменты относительно его оси – скручивающие нагрузки. Внутреннее усилие при кручении – крутящий момент. Дифференциальное соотношение между крутящим моментом и распределенной скручивающей нагрузкой: dMк/dz = -m              20.Расчет стержней круглого сечения на прочность и жесткость. Условие прочности при кручении круглых сечений по допустимым напряжениям:                       Расчет стержней на жесткость                     21.Изгиб стержней. Основные понятия. Изгиб – вид деформации стержня, при к-м внешние нагрузки действуют перпендикулярно к его оси. Стержень, работающий на изгиб, - балка. Виды изгиба: 1) Пространственный – нагрузки лежат в разных плоскостях.(два изгибающих момента y, z; две поперечные силы y, z)2) Плоский – внешние нагрузки лежат в одной плоскости. 3)Плоский прямой – плоскость действия нагрузок проходит через одну из главных центральных осей сечения. (два усилия – изгибающий момент и поперечная сила) 4) Плоский косой – плоскость действия нагрузок не проходит ни через одну из главных осей сечения.(два изгибающих момента y, z; две поперечные силы y, z) 22.Плоский прямой изгиб. Внутренние усилия. Дифференциальные соотношения. Построение эпюр поперечных сил и изгибающих моментов. Плоский прямой – плоскость действия нагрузок проходит через одну из главных центральных осей сечения. Возникают два усилия (в случае отсутствия осевых нагрузок) – изгибающий момент и поперечная сила) Момент положительный, если вызывает растяжение нижних волокон балки; отрицательный – растяжение верхних. Поперечная сила считается положительной, если она стремится повернуть рассматриваемую часть балки по ходу часовой стрелки. Для определения внутренних усилий используется метод сечений. dQy/dx=-q dMz/dx=Qy d2Mz/dx2=-q При построении эпюр положительное направление ОУ выбирать сверху вниз, на эпюре Q положительные ординаты откладывать вниз, отрицательные – вверх; Ординаты эпюры М откладывать со стороны растянутых волокон, следовательно положительные значения откладываются вниз, отрицательные – вверх. q=0; Qy – постоянна, а Mz – по линейному закону q=const; Qy – по линейному закону; Mz – по закону квадратной параболы, обащенной выпуклостью в сторону действия нагрузки q Где поперечная сила пересекает ось балки, изгибающий момент имеет экстремум В т-ке приложения сосредоточенной силы эпюра поперечной силы имеет скачок на величину приложенной нагрузки, а эпюра изгибающих моментов излом В т-ке приложения сосредоточенного момента на эпюра изгибающего момента скачок на величину приложенного момента 23.Нормальные напряжения при чистом изгибе. Нормальные и касательные напряжения при поперечном изгибе. Чистый изгиб – изгибающий момент имеет постоянное значение, а поперечная сила отсутствует. Угловые деформации в плоскости чистого изгиба отсутствуют, и поперечные сечения балки при деформации не искривляются. Нейтральный слой – слой, не испытывающий деформаций растяжения и сжатия. Нейтральная ось – линия пересечения нейтрального слоя с плоскостью поперечного сечения. Гипотезы: Поперечные сечения балки, плоские до деформации, остаются плоскими и ортогональными слою после деформации Взаимное давление между продольными слоями отсутствует – волокна испытывают одноосное растяжение и сжатие При чистом изгибе нормальные напряжения в поперечном сечении стержня изменяются по линейному закону. У отсчитывается от главной оси oz, к-ая является нулевой линией. В точках нейтральной оси нормальные напряжения равны нулю, а наибольшее и наименьшее значение принимают в нижних и верхних волокнах, наиболее удаленных от нейтральной оси.  Ф-ла Журавского для определения касательных напряжений при поперечном изгибе:    -для симметричных -для симметричных – для не симметричных – для не симметричных24.Анализ напряженного состояния в балках при изгибе. Главные напряжения. Нормальные напряжение при поперечном изгибе в продольных волокнах изменяются по длине балки. При поперечном изгибе в сечении балки действуют касательные напряжения, равнодействующая к-х явл поперечная сила. Наличие касательных напряжений сопровождается появлением угловых деформаций, к-ые неравномерно распределены по сечению. Наибольший сдвиг имеет место около нейтрального слоя. Особенность поперечного изгиба – наличие нормальных напряжений у, действующих в продольных волокнах балки и характеризующих взаимное давление между продольными слоями. Следовательно, в случаях поперечного изгиба малый элемент находится в условиях двухосного напряженного состояния.  25.Условия прочности. Расчет балок на прочность при изгибе. Наибольшие напряжения, возникающие в балке, не должны превышать некоторой допустимой для данного материалы величины. По первой группе предельных состояний(для пластичных):  -для симметричных -для симметричных – для не симметричных – для не симметричныхПо допускаемых напряжений(для пластичных):  26.Работа внешних сил и потенциальная энергия деформации при изгибе стержней и стержневых систем. Теоремы Бетти и Максвелла.                      В процессе деформирования она как бы накапливается в упругой системе, а при разгрузке затрачивается на возвращение ее в первоначальное недеформированное состояние. Теорема Бетти: Работа первой силы на перемещении по ее направлению от действия второй силы равна работе второй силы на перемещении по ее направлению от действия первой силы.  Теорема Максвелла: Перемещение по направлению действия второй силы в первом единичном состоянии равно перемещению по направлению действия первой силы во втором единичном состоянии.  27.Формула Мора для определения перемещений. Правило Верещагина.                  Правило Верещагина: Метод Верещагина заключается в “перемножении” эпюр грузового и единичного состояний. Правило Верещагина нельзя применять в случае, когда обе эпюры грузового и единичного состояний являются нелинейными(например, для стержней с криволинейной осью). Результат перемножения двух эпюр равен произведению площади одной эпюры на ординату под ее центром тяжести во второй эпюре. Если результаты перемножения двух эпюр – положительные, значит, что направления перемещений соответствует направлениям действия единичных нагрузок. Формула :  Ωp – площадь грузовой эпюры. EJ – жесткость 28.Кинематический анализ стержневых систем. Геометрически изменяемые, неизменяемые и мгновенно-изменяемые системы.  Геометрически неизменяемые системы — это системы соединенных между собой твердых тел (элементов систем), допускающие изменение формы только при деформации элементов. Геометрически изменяемые системы — это системы соединенных между собой твердых тел, допускающие конечные относительные перемещения тел без их деформации. Мгновенно изменяемые системы — это системы соединенных между собой твердых тел, допускающие бесконечно малые относительные перемещения тел без деформации 29. Степень свободы. Степень статической неопределимости. Принцип формирования геометрически неизменяемых систем. Степенью свободы системы C * называют число независимых параметров, определяющих положение системы относительно земли. При задании этого положения все элементы системы рассматривают как недеформируемые, т. е. как диски Статически неопределимые системы - Системы, в к-х число наложенных связей больше чем уравнений равновесия. Должны быть геометрически неизменяемые. Степень статической неопределимости – разность между числом неизвестных и числом независимых уравнений равновесия, к-ые можно составить для данной системы. Принцип формирования геометрически неизменяемых систем. Узел и диск образуют неизменяемую систему, если узел присоединен к диску двумя стержнями, оси которых не расположены на одной прямой . Два диска образуют неизменяемую систему, если они соединены между собой с помощью: а) трех стержней, оси которых (или их продолжения) не пересекаются в одной точке и не параллельны б) одного шарнира и стержня, ось которого не проходит через центр этого шарнира в) одной жесткой связи 3. Три диска образуют неизменяемую систему, если они соединены между собой с помощью: а) трех шарниров, расположенных между каждой парой дисков так, чтобы центры этих шарниров не лежали на одной прямой б) шести стержней, каждые два из которых соединяют по паре дисков так, чтобы точки пересечения осевых линий стержней или их продолжений (будем называть их фиктивными шарнирами) также не лежали на одной прямой в) частично с помощью шарниров и частично с помощью стержней — смешанное соединение; при этом реальные и фиктивные шарниры не должны лежать на одной прямой 30.Статически определимые стержневые системы. Классификация плоских стержневых систем (рамы, фермы). Распорные системы (рамы, трехшарнырные арки). Если внутренние силы, действующие в неизменяемой механической системе, находящейся в равновесии, при любых нагрузках и недеформированном состоянии элементов системы определяются из уравнений статики для системы или отдельных ее частей, то такая система называется статически определимой Классификация: Рамы: Балочные Арочные Рамные Рамно-связные Комбинированные Пространственные Фермы Распорные системы – конструкции, имеющие несменяемые опоры. За счет этого при деформации конструкции под действием нагрузки возникает распор, к-й создает в конструкции продольные усилия. Жесткие распорные конструкции (рамы, арки, оболочки) отличаются пониженной деформативностью по сравнению с безраспорными, что позволяет уменьшать размеры сечение их элементов. 31. Расчет статически неопределимых стержневых систем методом сил. Степень статической неопределимости. Основная система метода сил. Расчет статически неопределимых стержневых систем методом сил. 1) Установить степень статической неопределимости системы n; 2) Выбрать основную систему, удалив n лишних связей с заменой каждой из них реактивным усилием Х (при n=1 удалить 1 лишнюю связь и заменить ее реактивным усилием Х1) 3) Построить в основной системе n единичных эпюр Мi от каждого реактивного усилия Хi = 1 (при n =1 построить единичную эпюру M1 От реактивного усилия Х1) Определить коэффициенты системы канонических уравнений  ( при n = 1 опр коэф ( при n = 1 опр коэф  ) )Построить в основной системе эпюру Мр(грузовую эпюру) от приложенных к системе внешних нагрузок Определить перемещения  (при n=1 определить перемещение (при n=1 определить перемещение  ) )Записать систему канонических уравнений и решить ее, те определить значения неизвестных усилий Хi (при n=1 записать каноническое уравнение и определить значение неизвестного усилия Х1) Кинематическая проверка: перемещения по направлению удаленных связей при составлении канонических уравнений приравнивается к нулю, соответствующие интегралы Мора также должны быть равны нулю. Степень статической неопределимости: n= p – k , p – количество неизвестных; k – количество уравнений статики(3 -плоская система; 6 -пространственная стержневая система) n=0 – статически определимая система n=-W определение степени свободы стержневой системы Основная система метода сил – любая статически определимая система, полученная из заданной статически неопределимой удалением лишних связей 32. Канонические уравнения метода сил. Статическая и кинематическая проверка результатов.   При статической проверке, выполняемой обычно для рам, вырезаются узлы и записываются условия их равновесия под действием узловых сосредоточенных моментов и изгибающих моментов на концах стержней. Смысл кинематической проверки состоит в подтверждении отсутствия перемещений в основной системе в направлении отброшенных (перерезанных) связей при найденных значениях неизвестных усилий. Так, если неизвестные усилия найдены правильно, то для рассматриваемого примера должны удовлетворяться равенства:  33. Устойчивость стержней. Виды равновесия тел. Продольный изгиб. Устойчивое равновесие – равновесие, при к-м тело после малого отклонения от исходного положения возвращается в это же положение при устранении воздействия, вызывающего это отклонение. Безразличное – когда тело после отклонения остается в равновесии и в новом положении. Неустойчивым – когда тело при малом отклонении не возвращается в исходное положение, а удаляется от него. Продольный изгиб – явление, при к-м после приложения к стержню силы, равной критической или превышающей ее, происходит потеря устойчивости первоначальной прямолинейной формы равновесия, вследствие чего стержень изгибается. 34. Критическая сила. Определение критической силы. Влияние способов закрепления концов стержня на величину критической силы. Приведенная длина стержня. Коэффициент приведения длины. Критическая сила – наименьшая величина нагрузки, при к-й первоначальной формы равновесия становится неустойчивой. О  пределение критической силы: пределение критической силы:При небольших значениях Р ось стержня остается прямой и в его сечениях возникают напряжения центрального сжатия  . При критическом значении Р=Ркр становится возможной слегка искривленная форма равновесия стержня. Возникает продольный изгиб. Изгибающий момент в произвольном сечении х стержня равен: . При критическом значении Р=Ркр становится возможной слегка искривленная форма равновесия стержня. Возникает продольный изгиб. Изгибающий момент в произвольном сечении х стержня равен:  , ,  – плечо . – плечо . Формула Эйлера:  Где  – приведенная длина, а – приведенная длина, а – коэффициент приведения, зависящий от способа закрепления концов стержня – величина обратная числу полуволн синусоиды, по к-й изогнется стержень. – коэффициент приведения, зависящий от способа закрепления концов стержня – величина обратная числу полуволн синусоиды, по к-й изогнется стержень.35. Критические напряжения. Пределы применимости формулы Эйлера.    – гибкость стержня – отношение приведенной длины стержня к радиусу поперечного сечения стержня – гибкость стержня – отношение приведенной длины стержня к радиусу поперечного сечения стержняУсловие применимость ф-лы Эйлера:  , где , где  – предельная гибкость, если – предельная гибкость, если  -если условие выполняется стержень большой гибкости -если условие выполняется стержень большой гибкостиФ-ла Ясинского:   – для пластичных; – для пластичных; - для хрупких - для хрупкихУсловие применимости: если   -для хрупких -для хрупких -для пластичных -для пластичныхДля материалов малой гибкости: Стержни, у к-х  – стержни малой гибкости. Они могут разрушаться не результате потери устойчивости, в результате потери прочности при центральном сжатии – стержни малой гибкости. Они могут разрушаться не результате потери устойчивости, в результате потери прочности при центральном сжатии – для пластичных; – для пластичных; - для хрупких - для хрупкихПри продольном изгибе центрально сжатый стержень теряет несущую способность, когда напряжения в его поперечных сечениях становятся равными критическим. Условие устойчивости при расчете по методу предельных состояний  , где , где  - коэф уменьшения расчетного сопротивления при продольном изгибе(коэф продольного изгиба) - коэф уменьшения расчетного сопротивления при продольном изгибе(коэф продольного изгиба) -по строительным нормам. -по строительным нормам. |
