Математические структуры данных. Задача на минимум Начальная симплекстаблица f 1 1 1

• Название: Задача на минимум Начальная симплекстаблица f 1 1 1
• Анкор: Математические структуры данных
• Дата: 27.10.2022
• Размер: 39.66 Kb.
• Имя файла: LR_2.docx
• Тип: Задача; #757778
• страница: 5 из 5

В качестве базисной переменной x7 берём x2 и считаем дельты

C	5	3	5	0	0	0	0	0	0	0
Базис	X1	X2	X3	X4	X5	X6	X7	X8	X9	b	Q
X1	1	0	0	1	0	0	0	0	0	1	-
X5	0	0	0	-1/5	1	0	-3/5	0	1/5	4/5	1
X6	0	0	0	-3/10	0	1	1/10	0	-1/5	7/10	-
X2	0	1	0	1/5	0	0	3/5	0	-1/5	1/5	1/5
X8	0	0	0	21/10	0	0	13/10	1	2/5	21/10	-
X3	0	0	1	3/10	0	0	-1/10	0	1/5	3/10	2
Δ	0	0	0	71/10	0	0	13/10	0	2/5	71/10

Отрицательные дельты отсутствуют -> решение оптимально

F = 5*1 + 3*1/5 + 5 * 3/10 = 71/10

x1 = 1, x2 = 1/5, x3 = 3/10, F = 71/10

Двойственная задача на максимум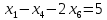

Исходная задача I		Двойственная задача II
x1 ≥ 0	↔	y1≥1
x2 ≥ 0	↔	y2≥1
x3 ≥ 0	↔	y3≥1
x4 ≥ 0	↔	-y1+2y2+2y3≥0
x5 ≥ 0	↔	-3y2-5y3≥0
x6 ≥ 0	↔	-2y1+y2+6y3≥0
x1+x2+x3 → max	↔	5y1+3y2+5y3 → min
x1-x4-2x6=5	↔	y1 любое число
x2+2x4-3x5+x6=3	↔	y2 любое число
x3+2x4-5x5+6x6=5	↔	y3 любое число

Т.к. ограничения содержат знак неравенства, базисной будет добавлены дополнительные переменные, построим начальную симплекс-таблицу.

C	5	3	5	0	0	0	0	0	0	0
Базис	X1	X2	X3	X4	X5	X6	X7	X8	X9	b
X4	-1	0	0	1	0	0	0	0	0	-1
X5	0	-1	0	0	1	0	0	0	0	-1
X6	0	0	-1	0	0	1	0	0	0	-1
X7	1	-2	-2	0	0	0	1	0	0	0
X8	0	3	5	0	0	0	0	1	0	0
X9	2	-1	-6	0	0	0	0	0	1	0
Δ	2	-1	-5	0	0	0	0	0	0	0

Вывод

В результате выполнения данной работы были найдены минимум и максимум функции симплекс-методом, а также графически найдены решения двух двойственных задач. Получилось убедиться, что если взаимно двойственные задачи имеют решения, то минимальное значение функции в одной задаче, равна максимальному значению функции в другой.