сопромат. ГТУ-19-1бзу. Задача Расчёты на прочность при сложном сопротивлении
 Скачать 328.5 Kb.
|
|
Вариант 14 Сопротивление материаловЗадача 4. Расчёты на прочность при сложном сопротивленииДля стального бруса с ломаной геометрической осью (рис. 4) определить внутренние усилия на каждом участке. Построить эпюры внутренних усилий (значения усилий в буквенном выражении), определить положения опасных сечений. Подобрать размеры поперечных сечений в виде прямоугольника с отношением сторон  , круга и кольца с отношением диаметров  . Размеры сечений округлить до стандартных значений.Дано: материал – Ст. 5:  МПа,  МПа, кН∙м,  кН/м,  м.Решение: В общем случае нагружения пространственного бруса в защемлении возникает шесть опорных реакций: три силы и три момента. Если определять внутренние усилия со свободного конца бруса, то нет необходимости в нахождении опорных реакций. Пронумеруем участки римскими цифрами I, II и III (рис. 4, а). В произвольном сечении каждого участка рассечем брус на две части. Отбросив ту из частей, где находится защемление, поместим в сечение координатную систему xyz. Из условия равновесия найдем внутренние усилия и результат запишем в таблицу. Для длинных балок (  ) влиянием поперечных сил Q обычно пренебрегают, поскольку касательные напряжения τ от Q на порядок меньше нормальных σ от M. Знаки внутренних усилий устанавливаем согласно правилам теоретической механики: если при взгляде в торец отсеченной части бруса внутренний момент, уравновешивающий внешнюю нагрузку, вращает против хода часовой стрелки, то его считают положительным.Внутренние усилия в рассчитываемом ломаном брусе
Каждую из эпюр изгибающих моментов My и Mz построим в отдельности на растянутой части бруса (рис. 4, д, е). Эпюры крутящего момента Т и осевого усилия N целесообразно совместить (рис. 4, ж). Сопоставив эпюры внутренних усилий, можно заключить, что опасными являются следующие сечения: участок I – при  , изгиб в двух плоскостях;участок II – при , совместное действие изгиба и кручения;участок III – при любом  , изгиб, кручение и сжатие.Сечения не равноопасны! Для использования условия прочности на первом участке потребуется допускаемое напряжение на изгиб. На двух других участках ломаного бруса имеет место совместное действие изгиба и кручения. В этом случае эквивалентное напряжение, найденное по теориям прочности, сопоставляют с допускаемым, определённым при растяжении. Участок I Из условия прочности при плоском изгибе определяем требуемое значение момента сопротивления  , откуда  .Суммарный изгибающий момент в сечении определяется так  .Для сечения : кНм, кНм,Тогда  кНм.С учётом соотношения высоты прямоугольника к его ширине 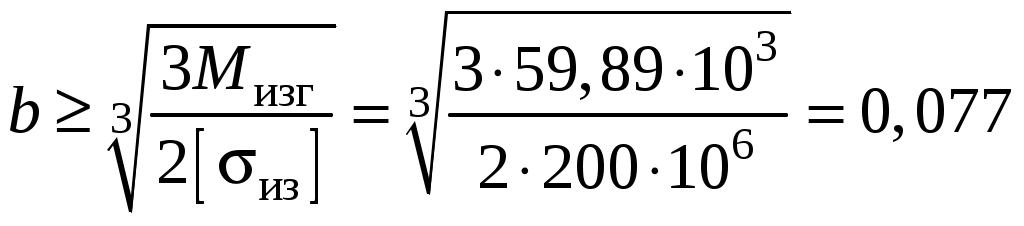момент сопротивления прямоугольного сечения , откуда  м.Округлив размер ширины до стандартного значения  мм, найдем высоту прямоугольного сечения  мм.Участок II Из условия прочности при изгибе с кручением находим требуемое значение момента сопротивления круглого сплошного сечения 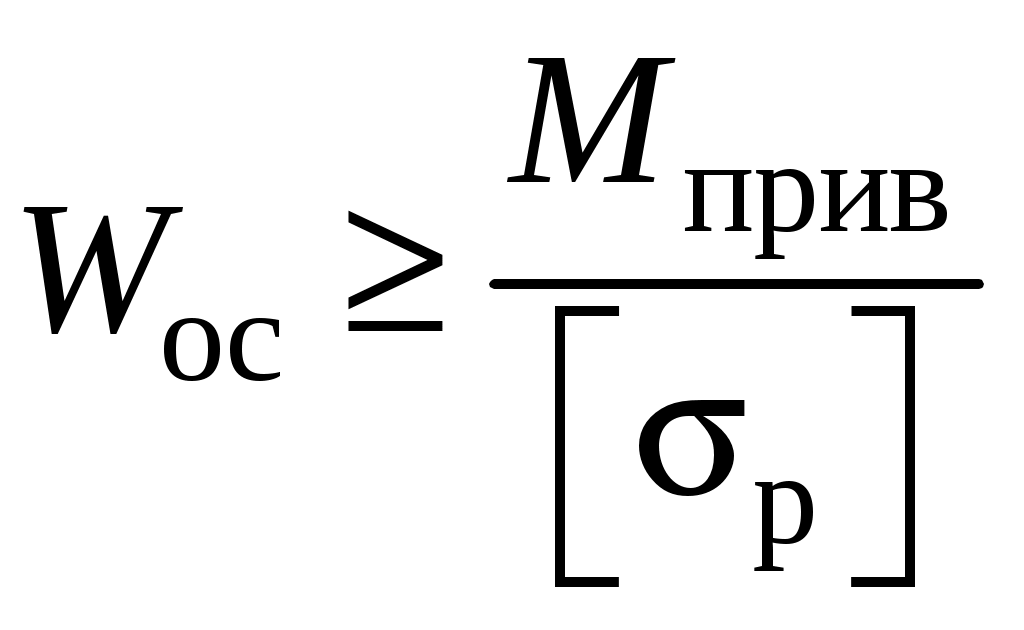 , откуда  .Осевой момент сопротивления для трубчатого сечения: 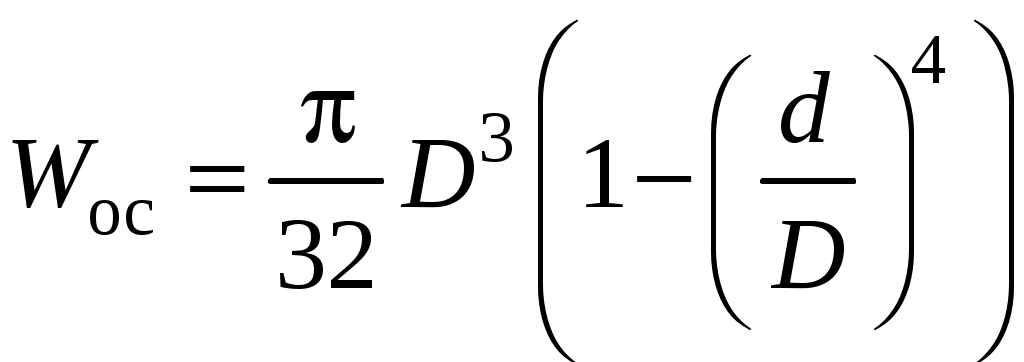 .При использовании III гипотезы прочности приведённый момент имеет вид  .Для сечения : кНм,  кНм, кНм.Тогда  кНм.Требуемый диаметр трубчатого поперечного сечения 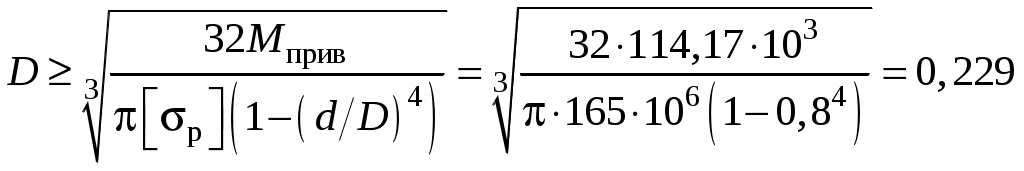 м.В соответствии с ГОСТ 6636–69 принимаем диаметр  мм.Участок III На участке действуют четыре внутренних усилия. Подбор сечения выполним из условия прочности при изгибе с кручением, то есть, учитывая два изгибающих Mz, My и крутящий T моменты, а при поверочном расчёте учтём ещё и продольное усилие N. Требуемый момент сопротивления 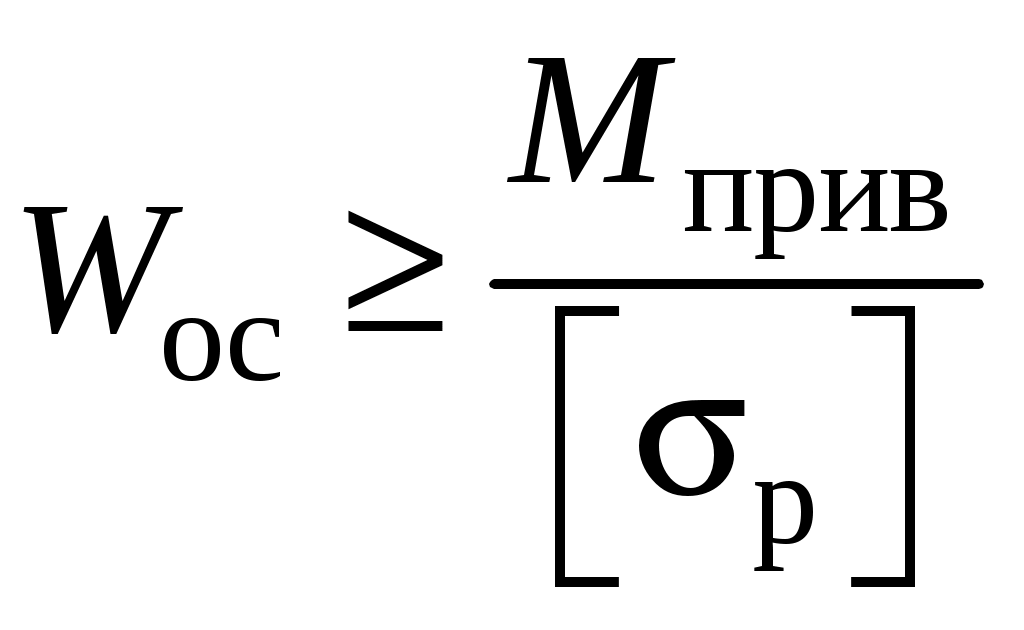, где тля круглого сечения  .Для данного участка  кНм,  кНм, кНм,  кН.Тогда  кНм.Требуемый диаметр круглого сечения 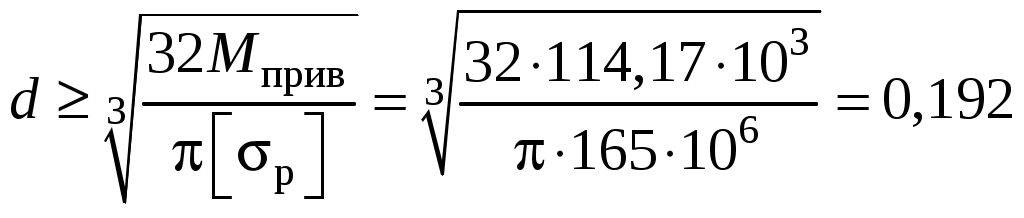 .Округлив до стандартного значения, получим  мм.Для полученного диаметра рассчитаем момент сопротивления и площадь сечения бруса на выбранном участке  м3, м2.Эквивалентные напряжения при этом составят  МПа  .Напряжения от действия продольной силы   МПа.Суммарное нормальное напряжение на участке составит  МПа .Как видно из поверочного расчёта, доля нормального напряжения, вызванная осевой силой N, незначительна. Поэтому при подборе размеров поперечного сечения осевой составляющей нагрузки в первом приближении часто пренебрегают. 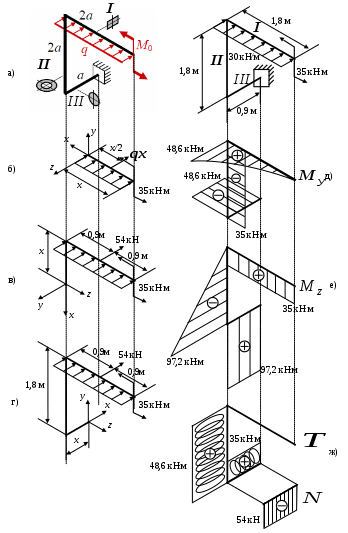 Рис. 4. | |||||||||||||||||||||||||||||||||||||||||||||||
участок 
участок 
участок 
