СМ__РГР_2. Задача Тема Плоский изгиб. Для заданной схемы балки (рисунок 3) требуется

• Название: Задача Тема Плоский изгиб. Для заданной схемы балки (рисунок 3) требуется
• Дата: 13.10.2022
• Размер: 173.7 Kb.
• Имя файла: СМ__РГР_2.docx
• Тип: Задача; #732315
• страница: 2 из 2

Третью задачу контрольной работы следует решать после изучения темы «Изгиб» и внимательного разбора примеров 5 и 6 настоящего пособия.

При прямом поперечном изгибе в поперечных сечениях балки возникает два внутренних силовых фактора – поперечная сила Q_y и изгибающий момент M_x. Поперечная сила, возникающая в произвольном поперечном сечении, численно равна алгебраической сумме всех внешних сил (если все силы параллельны оси y), действующих на балку по одну сторону от рассматриваемого сечения.

Изгибающий момент в произвольном поперечном сечении численно равен алгебраической сумме моментов всех сил, действующих на балку по одну сторонку от рассматриваемого сечения относительно той точки продольной оси балки, через которую проходит рассматриваемое сечение.

Для отыскания опасного сечения строят эпюры Q_y и M_x, используя метод сечения.

Условимся о правиле знаков: внешняя сила F, стремящаяся сдвинуть левую часть балки вверх относительно правой или (что то же самое) правую часть вниз относительно левой, вызовет возникновение положительной поперечной силы (рисунок 8, а).

В 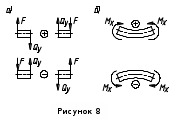нешняя сила или момент, изгибающие балку таким образом, что сжатые волокна находятся сверху балки (рисунок 8, б), вызывают положительный изгибающий момент, который на эпюре M_x откладывается вверх от оси абсцисс, т.е. в сторону сжатых волокон, иначе можно сказать, что эпюры изгибающих моментов строятся на сжатом волокне.

Для балок, имеющих много участков нагружения, т.е. нагруженных комбинацией нагрузок, целесообразно строить эпюры по характерным сечениям, а именно: вычислять поперечные силы и изгибающие моменты только для сечений, в которых эпюры претерпевают изменения, а затем, зная закон изменения эпюры между найденными сечениями, соединить их соответствующими линиями. К характерным сечениям относятся сечения, в которых приложены сосредоточенные силы или моменты, а так же сечения, где начинается или кончается распределенная нагрузка.

Для того чтобы вычислить поперечную силу и изгибающий момент в произвольном сечении, необходимо мысленно рассечь плоскостью в этом месте балку и часть балки (любую), лежащую по одну сторону от рассматриваемого сечения, отбросить. Затем по действующим на оставленную часть балки внешним силам надо найти искомые значения Q_y и M_x, причем знак их надо определить по тому действию, которое оказывают внешние силы на оставленную часть балки в соответствии с принятым ранее правилом знаков.

При построении эпюры слева на право отбрасывается правая часть балки, а Q_y и M_x находятся по силам, действующим на левую часть. При построении эпюры справа налево, наоборот, отбрасывается левая часть, а Q_y и M_x определяются по силам, действующим на правую часть балки.

Для построения эпюр необходимо запомнить следующие правила:

• 
  на участке балки, где отсутствует распределенная нагрузка, эпюра Q_y – прямая, параллельная базовой линии, а эпюра M_x – наклонная прямая;
  

• 
  под сосредоточенной силой на эпюре Q_y наблюдается скачок, численно равный приложенной внешней силе, а на эпюре M_x – излом;
  

• 
  в точке приложения сосредоточенной парой сил на эпюре момента происходит скачок на размер момента этой пары, а эпюра Q_y не претерпевает изменения;
  

• 
  на участке действия равномерно распределенной нагрузки эпюра Q_y выражается наклонной прямой, а эпюра M_x – параболой, обращенной выпуклостью навстречу действию распределенной нагрузки;
  

• 
  если на участке действия распределенной нагрузки эпюра пересекает базовую линию, то в этом сечении изгибающий момент принимает экстремальное значение;
  

• 
  если на границе действия распределенной нагрузки не приложено сосредоточенных сил, то на эпюре Q_y участок, параллельный оси абсцисс, переходит в наклонный без скачка, а параболическая и наклонная части эпюры M_x сопрягаются плавно без изгиба;
  

• 
  изгибающий момент в концевых сечениях балки всегда равен нулю, за исключением случая, когда в концевом сечении действует сосредоточенная пара сил. В этом случае изгибающий момент в концевом сечении балки равен моменту действующей пары сил.
  

В сечении, соответствующем заделке, Q_y и M_x численно равны опорной реакции и реактивному моменту.

Решать задачу рекомендуется в такой последовательности:

1. 
   определить реакции опор балки (по двум уравнениям моментов – одно относительно левой опоры, второе относительно правой), а затем обязательно проверить правильность решения по уравнению проекций на ось, перпендикулярную балке;
   
2. 
   построить эпюру поперечных сил;
   
3. 
   построить эпюру изгибающих моментов;
   
4. 
   по эпюре изгибающих моментов определить расчетный (наибольший по абсолютному значению) изгибающий момент, выразив его в ньютоно-метрах (Нм);
   
5. 
   в выражении условия прочности σ = М_и/W_x ≤ [σ] принять σ = [σ] и определить требуемый осевой момент сопротивления поперечного сечения балки;
   
6. 
   выразить значение W_x в м³ (при подстановке в расчетную формулу W_x = M_x/[σ] значения M_x выражаются в Нм, а значения [σ] – в Па, результат получим в м³) и с помощью таблиц соответствующих ГОСТов по найденному значению W_x подобрать необходимый размер прокатного профиля, используя ГОСТы, которые имеются в любом сборнике задач по сопротивлению материалов.
   

Пример 3.1. Для балки (рисунок 9, а) построить эпюры поперечных сил и изгибающих моментов, если сила F = 8 кН, интенсивность равномерно распределенной нагрузки q = 4 кН/м, момент М = 11 кНм, расстояние а = 2 м, b = 4 м, с = 3 м.

Решение. Определим опорные реакции: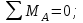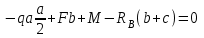
,

откуда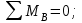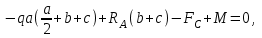




откуда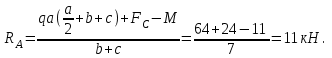


Для проверки составляем сумму проекций всех сил на вертикальную ось y: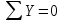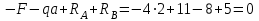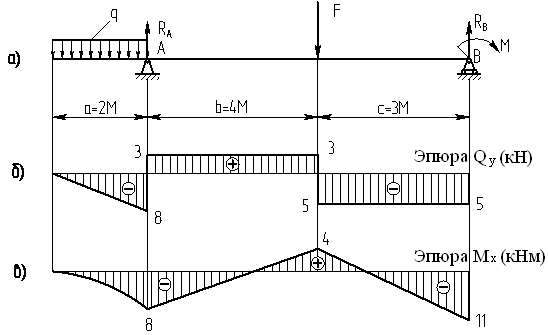
, .


Рисунок 9.
Строим эпюру поперечных сил (рисунок 9, б).

В сечении К:

Q_yK = 0.

В сечении А:

Q_yAлев = -qa = -42 = -8 кН;

Q_уАправ = -qa + R_A = -8 + 11 = 3 кН.
В сечении А на эпюре Q_y получается скачок на величину реакции R_A.

В сечении D:

Q_yDлев = qa + R_A = - 42 + 11 = 3 кН;

Q_yDправ = -qa + R_A – F = -8 +11 – 8 = -5 кН.

В сечении B:

Q_yB = -R_B = -5 кН.
Строим эпюру изгибающих моментов по характерным сечениям К, А, D, B (рисунок 9, в).

В сечении К изгибающий момент M_xK = 0, так как в этом сечении нет сосредоточенного момента.

В сечении А рассмотрим левую часть, на которую действует равномерно распределенная нагрузка: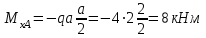

.

В сечении В действует сосредоточенный момент М: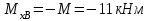

.

В сечении D рассмотрим правую часть, на которую действует сила R_B и сосредоточенный момент М: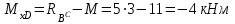

.

Соединим полученные точки эпюры на участках DB и AD наклонными прямыми, на участке АК – параболой, обращенной выпуклостью навстречу равномерно распределенной нагрузке.

Пример 3.2. Для балки (рисунок 10, а) простроить эпюры поперечных сил Q и изгибающих моментов М. а также определить из расчета на прочность размеры поперечного сечения круга диаметром d, кольца с отношением диаметров d/D = 0,9, прямоугольника соотношением сторон h/b = 2, номер профиля двутавровой прокатной балки. Собственную массу балки не учитывать.

Материал сталь – Ст3, [] =160 МПа, Е = 210⁵ МПа, М = 40 кНм, F = 20 кН м, q = 100 кН/м.

ПРИМЕЧАНИЕ: для решения задачи 3 из примера 3.2 выбрать только соответствующие условию задачи 3 расчёты.

Решение. 1. Построение эпюры Q и М начинаем с определения реакций опор А и В, для чего отбросим опоры А и В и балку представим как свободное тело, а действие опор на балку заменяем реакциями R_A и R_B (горизонтальная реакция - H_A в нашем случае эквивалентно нулю) (рисунок 10, б).

Таким образом, имеем два неизвестных - R_A и R_B, для нахождения которых необходимо составить два уравнения равновесия:



Уравнение моментов относительно опоры В позволяет определить реакцию R_A:

M_B = R_A6 - q34,5 + M + F2 = 0,

R_A = (10034,5 – 40 - 202)/6 = 212 кН.

Реакцию R_B определяем из условия равенства нулю суммы моментов относительно опоры А:

M_A = - R_B6 + q31,5 + M + F8 = 0,

R_B = (10031,5 + 40 + 208)/6 = 108 кН.

Проверка. Правильность нахождения реакций опор можно оценить, например, составив уравнение суммы проекций всех сил на ось Y:

Y = R_A - q3 + R_B – F = 0,

212 - 1003 +108 – 20 = 0,

320 – 320 = 0.

Балка состоит из четырех участков, в пределах которых выражения будут различны. Для составления аналитических выражений необходимо рассмотреть четыре сечения между силами: I-I сечения правее левой опоры; II-II сечение между концом пролета где действует распределенная нагрузка и моментом М; сечение III-III между моментом М и правой опоры В и четвертое сечение между правой опорой В и силой F.

Уравнения и для каждого участка имеет вид:

а) сечение I-I (0  z₁  3 м)

Q₁ = R_A – qz₁,

M₁ = R_Az₁ - qz₁²/2,

б) сечение II-II (3 м  z₂  4 м)

Q₂ = R_A – q3 (не зависит от z₂) ,

M₂ = R_Az₂ - q3(z₂ – 1,5),

в) сечение III-III (4 м  z₃  6 м)

Q₃ = R_A – q3 (не зависит от z₃) ,

M₃ = R_Az₃ - q3(z₃ – 1,5) + M,

г) сечение IV-IV (6 м  z₄  8 м)

Q₄ = R_A – q3 + R_B (не зависит от z₄) ,

M₄ = R_Az₄ - q3(z₄ – 1,5) + M + R_B(z₄ – 6),

Из полученных уравнений следует, что поперечная сила на первом участке изменяется по закону прямой, а на втором, третьем и четвертом участках постоянна.

Уравнения М показывают, что изгибающий момент на первом участке изменяется по закону параболы второго порядка, а на втором, третьем и четвертом участках - по закону прямой.

Для построения эпюры находим их числовые значения на границах участков, используя составленные уравнения:

а) сечение I-I (0  z₁  3 м)

при z₁ = 0 Q₁ = 212 кН, M₁ = 0,

при z₁ = 3 м Q₁ = - 88 кН, M₁ = 186 кНм.

Найдем экстремального значения момента на участке I-I. Для этого возьмем первое производную M₁ по z₁ и приравняв ее нулю, найдем положение сечения с экстремальным значением М₁:

dM₁/dz₁ = R_A –qz₁^* = 212 – 100z₁^* = 0,

откуда

z₁^* = 2,12 м.

Подставив значение z₁^* = 2,12 м в уравнение М₁ найдем величину экстремального момента

M_{1, max} = 2122,12 - 502,12² = 225 кНм;

б) сечение II-II (3 м  z₂  4 м):

при z₂ = 3 м Q₂ = – 88 кН, M₂ = 186 кНм,

при z₂ = 4 м Q₂ = – 88 кН, M₂ = 98 кНм,

в) сечение III-III (4 м  z₃  6 м):

при z₃ = 4 м Q₃ = - 88 кН, M₃ = 138 кНм,

при z₃ = 6 м Q₃ = - 88 кН, M₃ = - 38 кНм,

г) сечение IV-IV (6 м  z₄  8 м):

при z₄ = 6 м Q₄ = 20 кН, M₄ = - 38 кНм,

при z₄ = 8 м Q₄ = 20 кН, M₄ = 0.

Откладывая вычисленные значения Q и М в соответствующих характерных сечениях базисной линии, строим эпюры. Вид полученных эпюр показан на рисунках 10 в, г.



2. Проектный расчет, т.е. определение размеров поперечных сечений. Минимально допустимый момент сопротивления сечения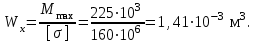



Для круглого сечения: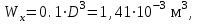



откуда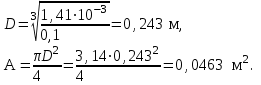



Для кольцевого сечения: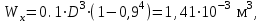



откуда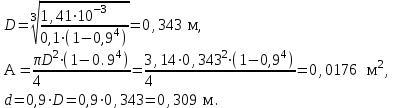



Для прямоугольного сечения: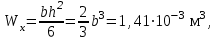



откуда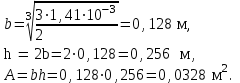



Определяем номера двутаврового сечения (ГОСТ 8239-72). Из таблицы сортамента выбираем двутавр № 50:

W_х = 1570 см³ = 1,5710^-3 м³; A = 97,8 см² = 0,00978 м².
Анализ найденных значений площадей сечения А показывает, что наиболее экономичным (минимальная масса) является профиль двутаврового сечения.