Задачи по электротехнике Вариант 18 Раздел ПЕРВЫЙ. Задачи по электротехнике Задание Расчет эквивалентных параметров соединений элементов

• Название: Задачи по электротехнике Задание Расчет эквивалентных параметров соединений элементов
• Дата: 08.06.2022
• Размер: 0.68 Mb.
• Имя файла: Задачи по электротехнике Вариант 18 Раздел ПЕРВЫЙ.docx
• Тип: Документы; #579055
• страница: 3 из 4

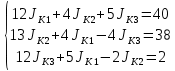Упорядочим систему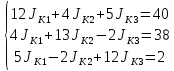

Решение системы линейных уравнений методом подстановки:

Решим систему уравнений:

	12Jк1 + 4Jк2 + 5Jк3 = 40
	4Jк1 + 13Jк2 - 2Jк3 = 38
	5Jк1 - 2Jк2 + 12Jк3 = 2

1-ое уравнение поделим на 12,и выразим Jк₁ через остальные переменные

	Jк1 = - (1/3)Jк2 - (5/12)Jк3 + (10/3)
	4Jк1 + 13Jк2 - 2Jк3 = 38
	5Jк1 - 2Jк2 + 12Jк3 = 2

в 2, 3 уравнение подставляем x1

	Jк1 = - (1/3)Jк2 - (5/12)Jк3 + (10/3)
	4( - (1/3)Jк2 - (5/12)Jк3 + (10/3)) + 13Jк2 - 2Jк3 = 38
	5( - (1/3)Jк2 - (5/12)Jк3 + (10/3)) - 2Jк2 + 12Jк3 = 2

после упрощения получим:

	Jк1 = - (1/3)Jк2 - (5/12)Jк3 + (10/3)
	(35/3)Jк2 - (11/3)Jк3 = 74/3
	- (11/3)Jк2 + (119/12)Jк3 = -44/3

2-ое уравнение поделим на 35/3,и выразим Jк₂ через остальные переменные

	Jк1 = - (1/3)Jк2 - (5/12)Jк3 + (10/3)
	Jк2 = (11/35)Jк3 + (74/35)
	- (11/3)Jк2 + (119/12)Jк3 = -44/3

в 3 уравнение подставляем x2

	Jк1 = - (1/3)Jк2 - (5/12)Jк3 + (10/3)
	Jк2 = (11/35)Jк3 + (74/35)
	- (11/3)( (11/35)Jк3 + (74/35)) + (119/12)Jк3 = -44/3

после упрощения получим:

	Jк1 = - (1/3)Jк2 - (5/12)Jк3 + (10/3)
	Jк2 = (11/35)Jк3 + (74/35)
	(1227/140)Jк3 = -242/35

3-ое уравнение поделим на 1227/140,и выразим Jк₃ через остальные переменные

	Jк1 = - (1/3)Jк2 - (5/12)Jк3 + (10/3)
	Jк2 = (11/35)Jк3 + (74/35)
	Jк3 = - (968/1227)

Теперь двигаясь от последнего уравнения к первому можно найти значения остальных переменных.

	Jк1 = 3730/1227=3,03993 А
	Jк2 = 2290/1227=1,86634 А
	Jк3 = -968/1227=-0,7889 А

Определим токи:

I1=	Jк1+Jк3	2,251	А
I2=	Jк1+Jк2	4,9063	А
I3=	Jк1	3,0399	А
I4=	Jк2-Jк3	2,6553	А
I5=	Jк2	1,8663	А
I6=	-Jк3	0,7889	А

Проверка по первому закону Кирхгофа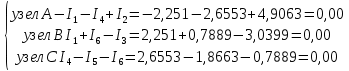



Проверка по второму закону Кирхгофа

I1*R1-I6*R6-I4*R4= E/1- E/4	2,251*5-0,7889*5-2,6553*2-2=0,00	условие выполнено
I1*R1+I3*R3+I2*R2= E1/+Е2	2,251*5+3,0399*3+4,9063*4-40=0,00	условие выполнено
I2*R2+I4*R4+ I5*R5= E4/+ Е2	4,9063*4+2,6553*2+1,8663*7-38=0,0	условие выполнено

4) выделим в схеме три сопротивления, включенные по схеме треугольника, и заменим их эквивалентным соединением по схеме звезды

Преобразованием треугольника в эквивалентную звезду называется такая замена части цепи, соединенной по схеме треугольником, цепью, соединенной по схеме звезды, при которой токи и напряжения в остальной части цепи сохраняются неизменными.

В данной схеме сопротивления R₃; R₅; R₆ включены по схеме треугольника.

Заменим их эквивалентным соединением по схеме звезды.


R₃₆

R₅₆

R₅₃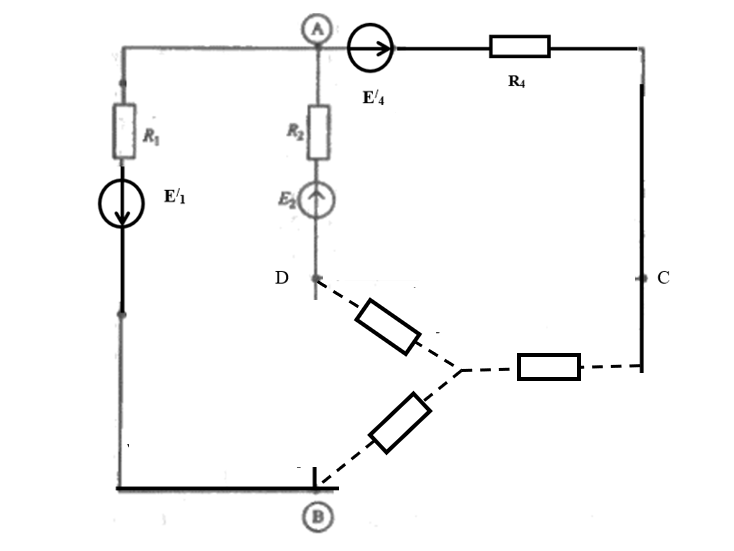


Найдем сопротивления в звезде: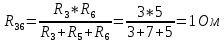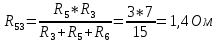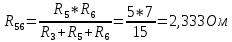







Преобразуем схему


R₅₆

R₅₃

R₃₆


Преобразуем схему суммируя последовательные соединения сопротивлений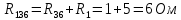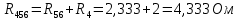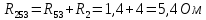







U₁₁

I₄

I₂

I₁

R₄₅₆

R₂₅₃

R₁₃₆

Сопротивления, Ом							Напряжения, В							Токи, А
R1	R2	R3	R4	R5	R6	Е1		Е2	Е3	Е4	Е5	Е6	J1		J2	J3	J4	J5	J6
5	4	3	2	7	5	0		20	0	0	0	0	4		0	0	9	0	0