Задачи по электротехнике Вариант 18 Раздел ПЕРВЫЙ. Задачи по электротехнике Задание Расчет эквивалентных параметров соединений элементов
 Скачать 0.68 Mb. Скачать 0.68 Mb.
|
|
5 Рассчитаем полученную схему методом узловых напряжений и найдем токи в ветвях Выполним расчет преобразованной схемы методом узловых напряжений. В полученной схеме имеются только два узла, поэтому для нее можно составить только одно уравнение по методу узловых напряжений: 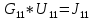 где U11 – узловое напряжение; 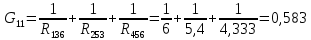 Ом-1 узловая проводимость; Ом-1 узловая проводимость;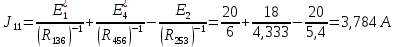 узловой ток источников. узловой ток источников.Подставив значение узловой проводимости G11 и узлового тока J11, найдем узловое напряжение. 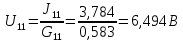 Используя значения узлового напряжения, найдем токи в ветвях: 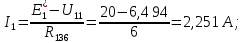 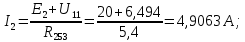 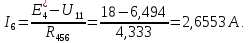 Сравнение результатов расчета токов I1, I2, I4 методами узловых напряжений и контурных токов показало их полное совпадение, что подтверждает корректность решения задачи. 6 Определим ток в сопротивлении R6 по методу эквивалентного генератора Для этого будем считать, что сопротивление R6 является нагрузкой, исключив его, разорвав ветвь, в которой оно было включено, как показано на рис. По теореме об эквивалентном генераторе ток в нагрузке можно найти по формуле: Uхх — напряжение холостого хода генератора; Rн — сопротивление нагрузки; Rг — сопротивление генератора относительно зажимов нагрузки. Найдем сопротивление генератора и напряжение холостого хода. При расчете эквивалентного сопротивления учтём, что внутреннее сопротивление источника ЭДС равно нулю, а сопротивление источника тока бесконечно. Рисуем схему эквивалентного генератора: 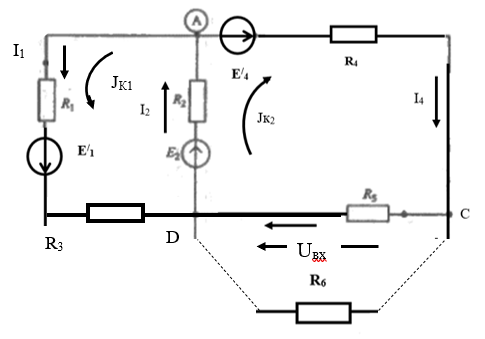 Преобразуем источники напряжения в источники тока              J/2 J/1 R2 R13  Найдем сопротивления: 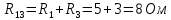 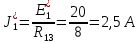 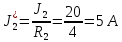 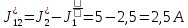 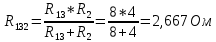 Преобразуем суммарный источник тока 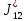 в источник напряжения: в источник напряжения: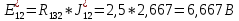 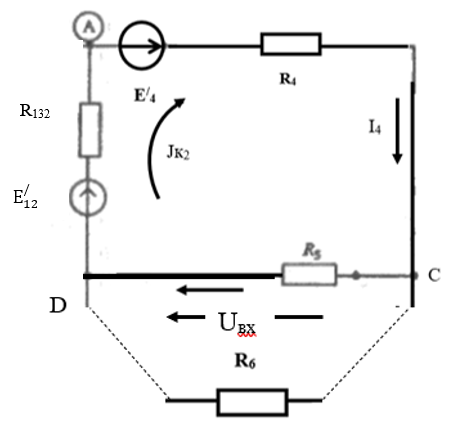 Определим ЭДС эквивалентного генератора. Исследуемая ветвь R6 исключается, и полученная схема показана на рисунке. Как видно из полученной схемы у нас осталось только два узла А и D, а точки С и B уже не являются узлами. Нам необходимо произвести расчет потенциалов в точках a и b. Напряжение между этими двумя точками является напряжением холостого хода, и оно равно ЭДС эквивалентного генератора. 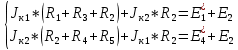 З 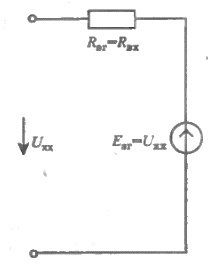 атем для полученной схемы найдем напряжение Uxx холостого хода и ее входное сопротивление Rвх между зажимами подключения нагрузки (т.е. сопротивление R6). В результате схема сводится к цепи, которая изображена на рис. атем для полученной схемы найдем напряжение Uxx холостого хода и ее входное сопротивление Rвх между зажимами подключения нагрузки (т.е. сопротивление R6). В результате схема сводится к цепи, которая изображена на рис. Найдем токи в ветвях цепи. Для этого воспользуемся методом контурных токов. Уравнение цепи, составленные по методу контурных токов, имеют вид:  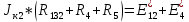 Подставим известные величины: 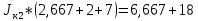 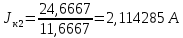  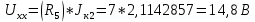 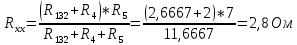 Теперь можно найти напряжение Uxx на зажимах подключения нагрузки: 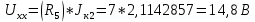 Для определения входного сопротивления Rвх необходимо исключить из схемы источники напряжения, заменив их перемычками. Для расчета входного сопротивления произведем замену R2, R4, R5 соединённые треугольником эквивалентной звездой/                                      R45 R25 R24 Uвх 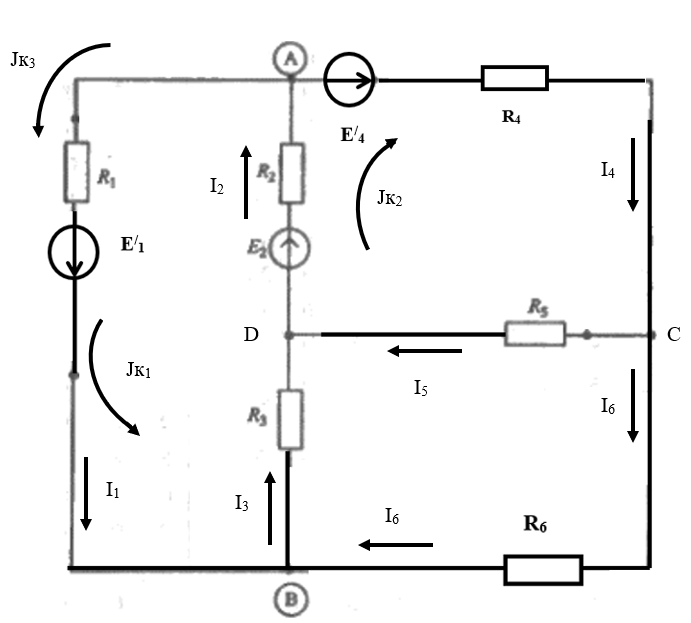  Найдем сопротивления в звезде: 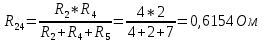 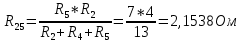 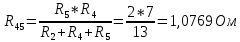 Суммируем последовательные сопротивления R1 и R24 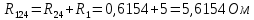 Суммируем последовательные сопротивления R3 и R25 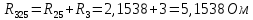 Получили параллельное соединение сопротивлений R124 и R325 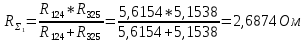 В полученной схеме сопротивления соединены последовательно. Суммируем последовательные сопротивления 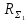 и R45 и R45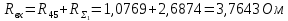 Найдем параллельное соединение 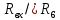
В заключение найдем ток в сопротивлении R6: 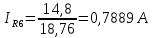 Полученный результат совпадает со значением тока I6 полученный ранее по методу контурных токов, что подтверждает правильность выполненного расчета. 7 Рассчитаем напряжение между точками А и В схемы Определим напряжение между точками А и В используя ранее произведенные расчеты.  Из схемы видно, что UAB равен напряжению на сопротивлении R1. Нам известен ток через R1 само сопротивление, значит будет равен: UAB= R1*Jк1=5*3,03993=15,2 B 8 Cоставим баланс мощностей для исходной схемы  Для любой, сколько угодно сложной цепи постоянного тока, можно составить энергетический баланс, вытекающий непосредственно из закона сохранения энергии: алгебраическая сумма всех мощностей источников энергии равна сумме всех мощностей приемников энергии: 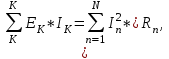 (3) (3) В этой формуле К − число источников энергии цепи; N – число приемников энергии цепи. Во всех приемниках энергии токи и напряжения имеют одно и то же направление. Поэтому правая часть уравнения (3) является арифметической суммой мощностей всех приемников цепи. Что касается левой части этого уравнения, то в некоторых ветвях сложной цепи ток ветви может оказаться направленным противоположно действию ЭДС источника энергии. Тогда произведение EI получается отрицательным. Физически это означает, что при таком режиме работы рассматриваемый источник не генерирует энергию, а потребляет ее (например, аккумулятор при его зарядке)
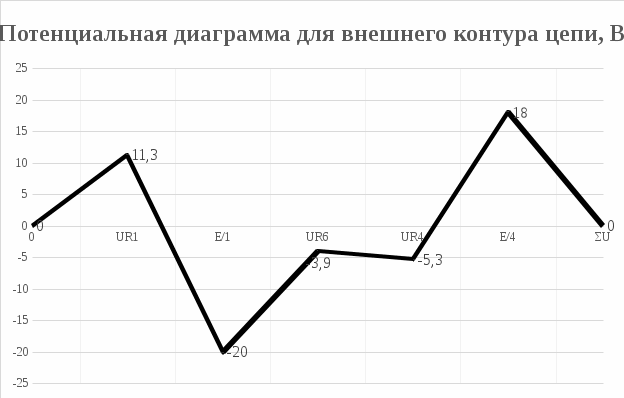
Погрешность расчета (небаланс) составила 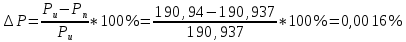 Как видим баланс мощностей сходится, значит расчет произведен верно. 9 Построим потенциальную диаграмму для внешнего контура цепи. Для этого запишем по второму закону Кирхгофа для внешнего контура: I1*R1+ Е/1—I6*R6—I4*R4—Е/4=0 2,251*5+20-0,7889*5-2,6553*2-18=0
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
