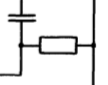
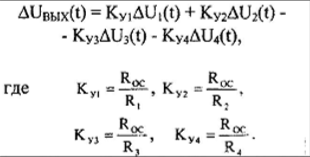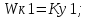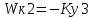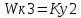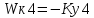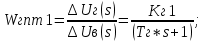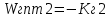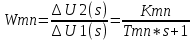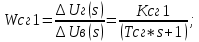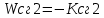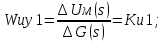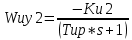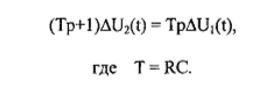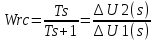САР напряжения синхронного генератора. РГР ТАУ. Задачи расчетнографической работы
 Скачать 1.14 Mb. Скачать 1.14 Mb.
|
|
Задачи расчетно-графической работы: 1. Дать краткое описание системы автоматического регулирования САР. 2. Используя линейные модели элементов САУ, составить по принципиальной с схеме системы функциональную и структурную схемы. 3. Описать принцип регулирования САР. 4. Получить передаточную функцию системы в разомкнутом состоянии Wрс(s). Найти передаточные функции замкнутой системы по задающему воздействию - gt Ws и возмущающему фактору – sW tf. 5. Записать дифференциальное уравнение САР. 6. Проверить САР на устойчивость по корням характеристического уравнения системы. 7. Проверить САР на устойчивость, используя критерий устойчивости Михайлова. 8. Проверить САР на устойчивость, используя критерий устойчивости Найквиста. Определить запасы устойчивости системы по модулю, амплитуде и фазе. 9. Определить по критерию устойчивости Гурвица критический коэффициент усиления разомкнутой системы Крс. 10. Построить область устойчивости в плоскости одного параметра – Крс. 11. Приняв начальные условия нулевыми, построить переходную характеристику системы и определить по ней показатели качества. 12. Определить полную установившуюся ошибку системы. Условия для проведения расчетов: «САР напряжения синхронного генератора» 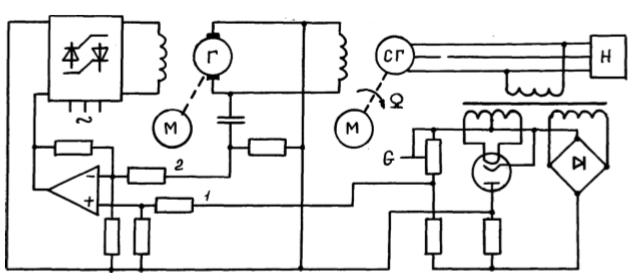 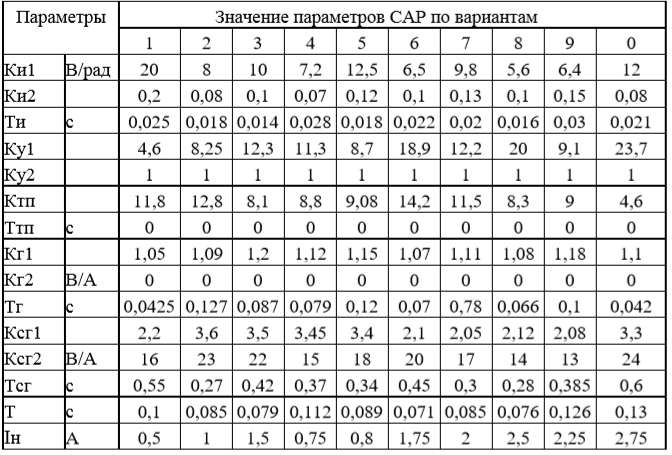 Приложение для выполнения курсовой работы:
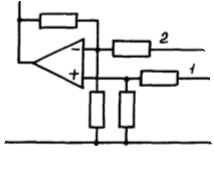
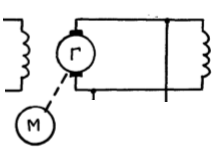
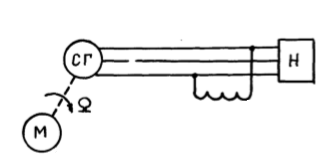
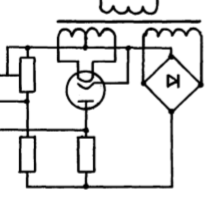
1. Создание функциональной схемы САР по принципиальной схеме. Любая функциональная схема САР по отклонению включает в себя объект управления – ОУ с выходной регулируемой величиной х(t) и возмущающим воздействием – f; устройство управления, обеспечивающее c заданной точностью стабилизацию выходной величины х т.е. x(t)=x0=const; задающее устройство, обеспечивающее необходимое значение x0 ; обратную связь; сравнивающее суммирующее устройство. В свою очередь устройство управления может состоять из усилительного элемента, исполнительного устройства и последовательной или параллельной коррекции. Кроме того, в САР возможно дополнительное регулирование по возмущающему фактору f, или задающему воздействию g либо одновременно по возмущающему фактору и задающему воздействиям (комбинированное управление).  Рис. 1 Принципиальная схема САР напряжения синхронного генератора 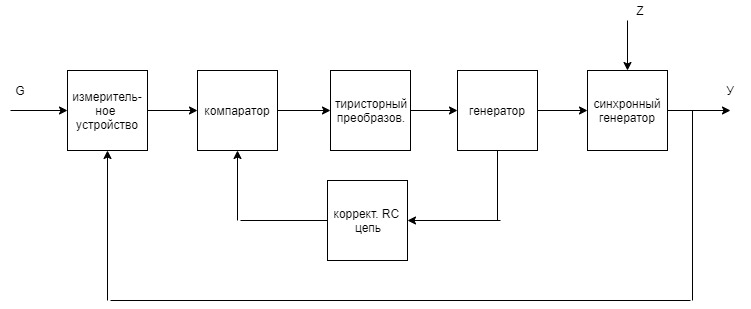 Рис.2. Функциональная схема 2. Создание структурной схемы САР Для составления структурной схемы необходимо по дифференциальным уравнениям (ДУ) элементов и устройств САР составить их передаточные функции. При этом, составляющую ДУ по возмущающему фактору f (Mc, Iн и т.п.) необходимо учитывать только для объекта управления ОУ. Поэтому ОУ будет иметь две передаточные функции (ПФ) по управляющему воздействию) (sW g oy и по возмущающему фактору) (sW f oy . Сравнивающие суммирующие устройства имеют тоже несколько передаточных функций и их количество определяется количеством входов. Для определения выражения передаточной функции по конкретному воздействию используется принцип суперпозиции. Передаточная функция есть отношение выходного сигнала в изображении s к входному при нулевых начальных условиях, либо отношение оператора правой части дифференциального уравнения к оператору левой части при замене р на s. 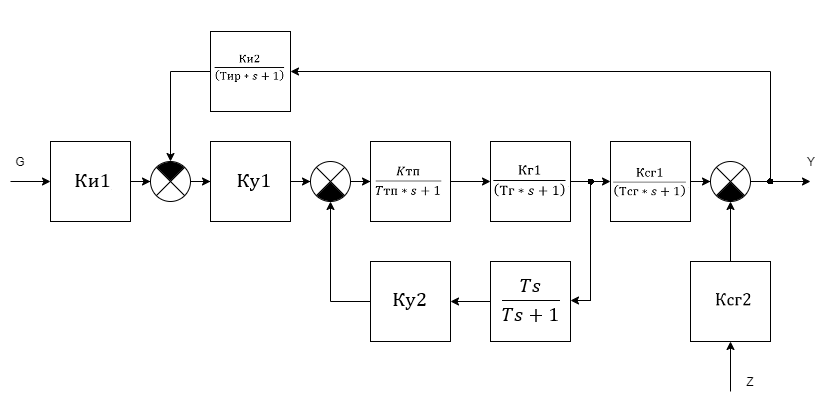 Рис.3. Структурная схема 3. Передаточные функции САР по задающему и возмущаемому воздействиям Определим ПФ контура с местной отрицательной обратной связью:  Передаточная функция по задающему воздействию будет иметь следующий вид: 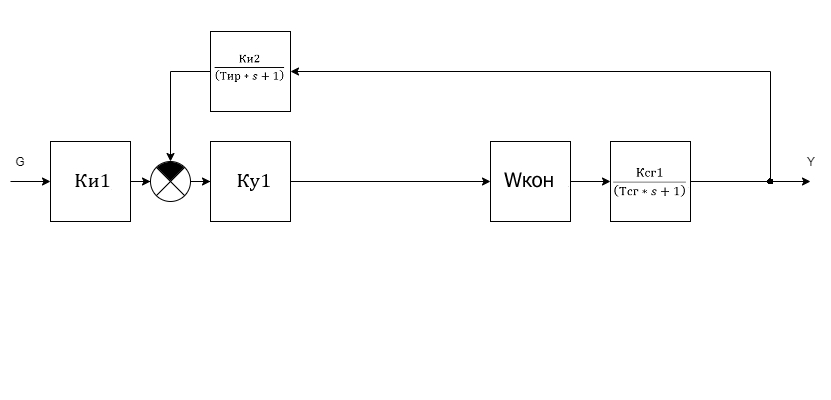  Передаточная функция системы по возмущающему воздействию будет иметь следующий вид: 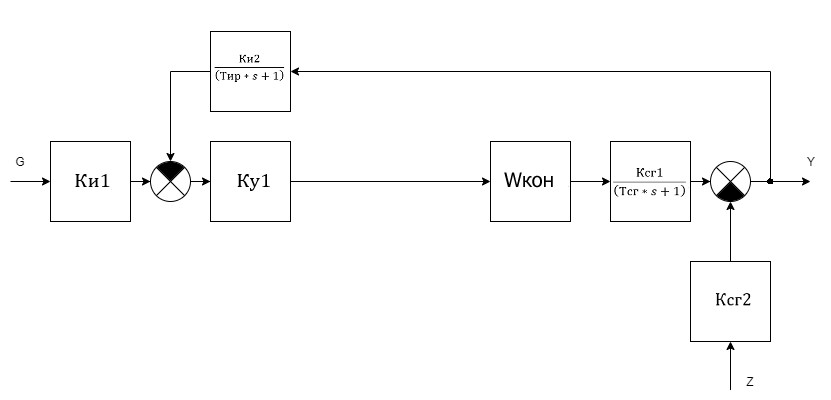  4. Дифференциальное уравнение САР Получив передаточные функции замкнутой системы по задающему и возмущающему воздействию, принципиальную схему САР, представленную на рисунке 3 можно изобразить следующим образом: 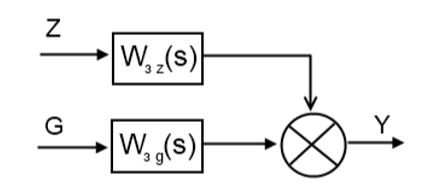 Рис.4. Структурная схема САР  5. Оценка устойчивости САР 5.1. Корневой метод. Запишем характеристическое уравнение системы: Найдем корни характеристического уравнения:  Все корни характеристического полинома имеют отрицательную действительную часть, следовательно, разомкнутая система устойчива. 5.2. Критерий устойчивости Михайлова Знаменатель передаточной функции замкнутой системы: Знаменатель передаточной функции замкнутой системы: Произведем замену s - jw. Получим:  Построим годограф Михайлова в среде MathCAD: 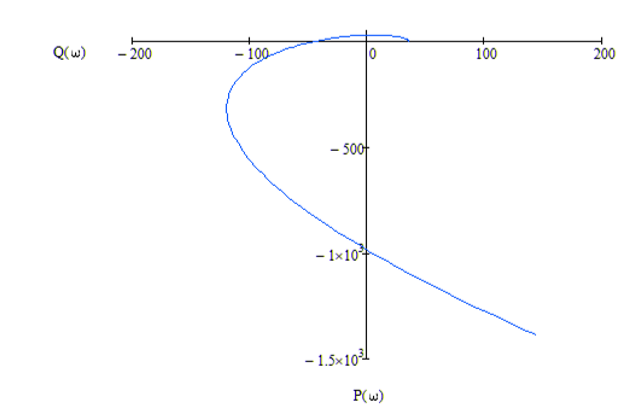 Рис.5. Годограф Михайлова Из представленных рисунков видно, что годограф Михайлова начинается на действительной положительной полуоси и последовательно проходит против часовой стрелки четыре квадранта (порядок системы так же равен n=4), что свидетельствует о том, что система устойчива. 5.3. Критерий устойчивости Найквиста 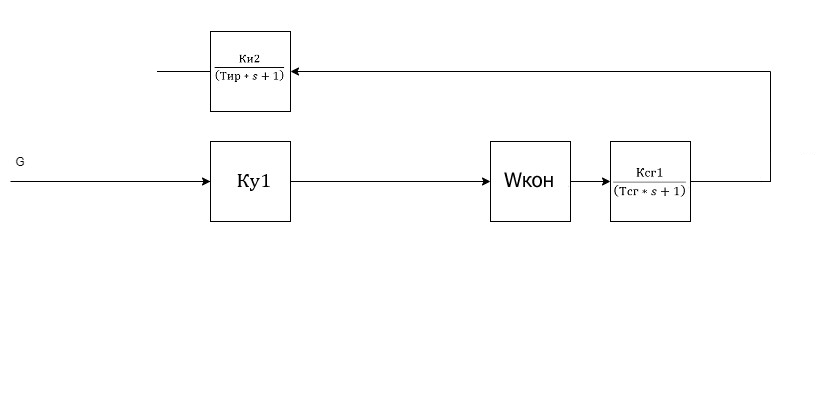 Рис 5.1 разомкнутая САР Для того чтобы оценить устойчивость системы по критерию Найквиста сначала найдем передаточную функцию разомкнутой системы:  Построим годограф Найквиста: 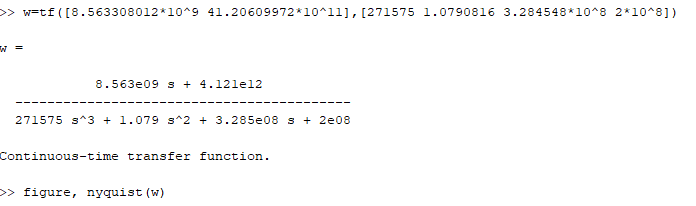 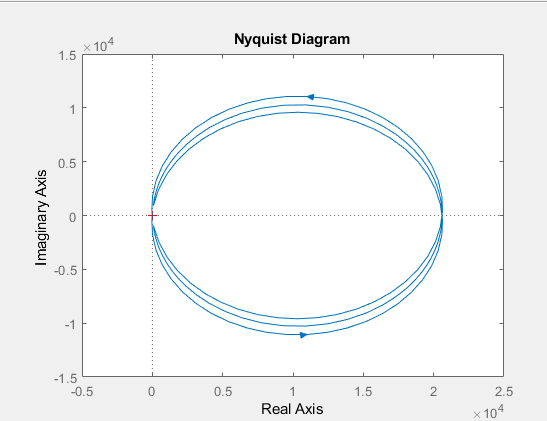 Годограф Найквиста разомкнутой системы не охватывает точку (-1; j0), следовательно, замкнутая система устойчива. 5.4. Критерий устойчивости Гурвица По критерию Гурвица, система со всеми положительными коэффициентами устойчива, если определители всех порядков матрицы Гурвица положительны.  Условие устойчивости выполняется; система устойчива. 6. Корневые показатели качества Время регулирования определяется по следующей формуле: 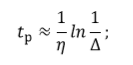 n=0.46 - степень устойчивости (минимальное расстояние от мнимой оси до ближайшего корня); Δ=5% дельта-зона; Используя полученные значения, рассчитаем время регулирования переходного процесса:  Определим степень колебательности:  Определим перерегулирование, которое характеризует склонность системы к колебаниям и связано со степенью колебательности следующим образом:  7. Построение области устойчивости в плоскости одного параметра. В качестве варьируемого параметра выберем коэффициент передачи генератора. Знаменатель передаточной функции замкнутой системы имеет следующий вид: Приравнивая полученное выражение к нулю, выразим Кгс к 0. Получим:  Для построения графика найдем действительную и мнимую часть полученного выражения:   Рис 8. Кривая D-разбиений 8. Запасы устойчивости. Колебательность САР Для определения запасов устойчивости САР построим логарифмические частотные характеристики по передаточной функции разомкнутой системы.  Рис.9. Логарифмические частотные характеристики системы Запас по амплитуде: 26 Дб Запас по фазе: 61.6* САУ, которая устойчива в разомкнутом состоянии, будет устойчивой и в замкнутом состоянии, если разница между количеством положительных и отрицательных переходов ЛФЧХ через прямую 180 градусов равна нулю в диапазоне частот, в котором ЛАЧХ положительная. ЛФЧХ проходит ниже линии φ= π. Запасом устойчивости по фазе является угол, соответствующий расстоянию от линии φ = π до ЛФЧХ. В системе матлаб определяется автоматически и выводится на график. Исследуемая САР обладает хорошими запасами по амплитуде и фазе, что является хорошим показателем для еѐ корректной работы. Для оценки колебательности САР вводят характеристику, которую называют показателем колебательности и определяется она следующим образом: По передаточной функции замкнутой системы построим амплитудно-частотную характеристику системы. Где А(w) – амплитуда гармонического сигнала в исследуемой системе (дБ), a w – его угловая частота (Гц). 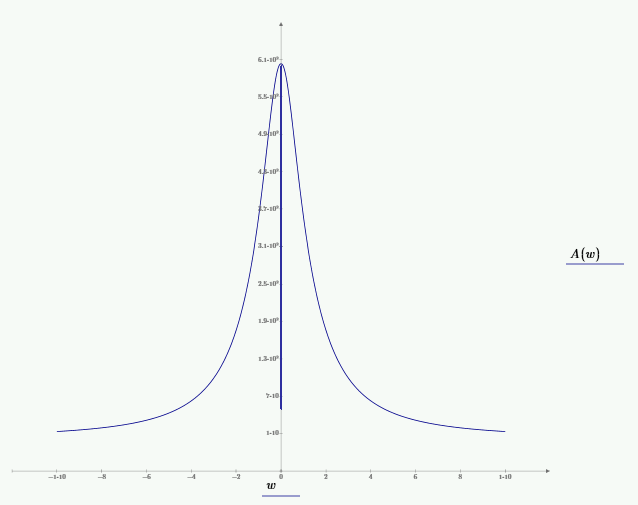 Рис.10. Амплитудно-частотная характеристика системы A0=50 Amax=600 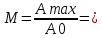 12 129. Переходные характеристики при нулевых начальных условиях. Прямые показатели качества. Для построения переходной характеристики соберем схему в пакете MatLAB Simulink: 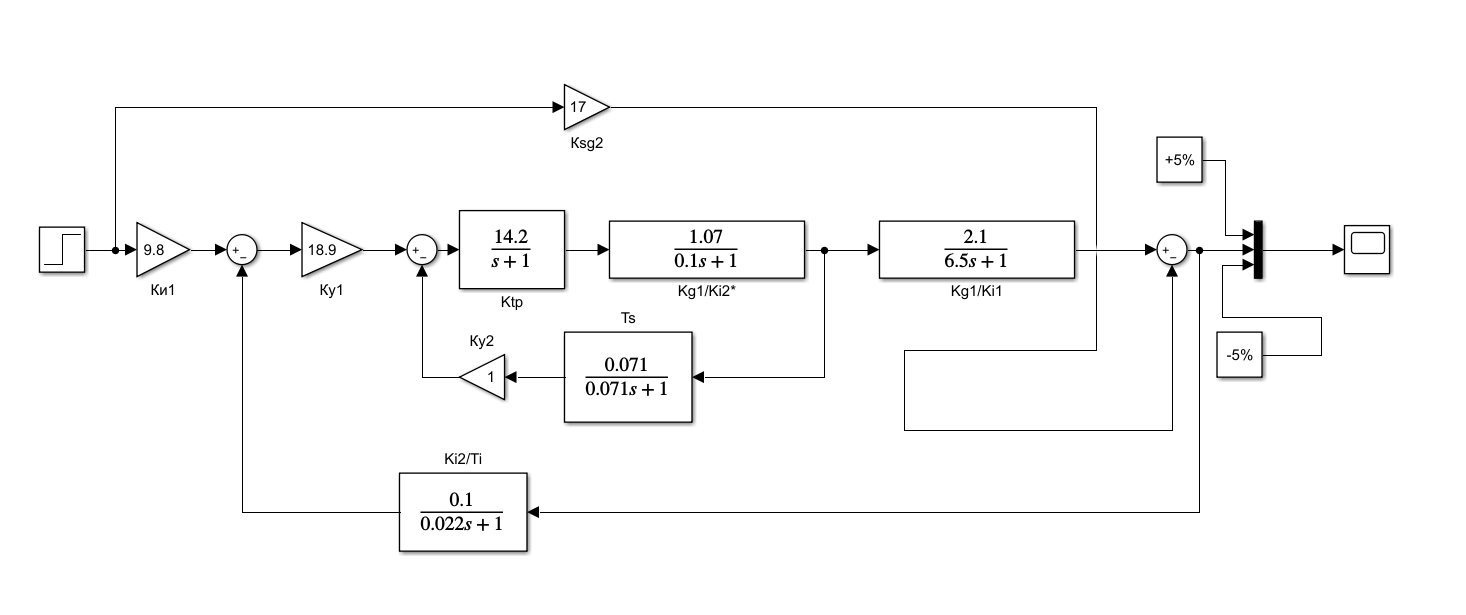 Рис.11. Модель системы в MatLAB Simulink 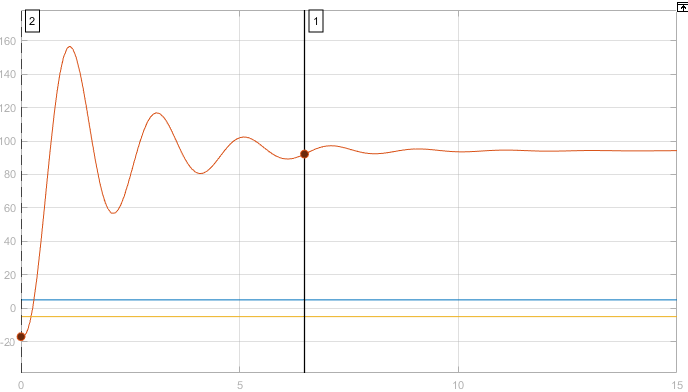 Определим показатели качества системы: Длительность фронта: tф = 1.2 ms Перерегулирование: hmax=156 hуст=94 q= 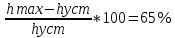 Время регулирования – время вхождения выходной величины в 5% коридор относительно установившегося значения:tp = 6.51 Характер переходного процесса: колебательный, сходящийся. По графику определяем, что установившееся значение переходной характеристики составляет 80. Следовательно, установившаяся ошибка при подаче на вход системы единичного ступенчатого сигнала: С0 = -0.2 Заключение В ходе выполнения расчетно-графической работы была проанализирована непрерывная, система автоматического регулирования, которая была составлена на основе принципиальной схемы «САР температуры в теплообменнике». Анализ системы был произведен на базе математических и теоретических сведений курса «Теория автоматического управления». После того, как на основе принципиальной схемы, была получена структурная схема, был произведен анализ системы на устойчивость, были определены прямые и корневые показатели качества. Анализ показал, что настоящая система автоматического регулирования с заданными параметрами является устойчивой, имеет сравнительно неплохие показатели качества, а так же запасы по амплитуде и фазе. Вычисления, произведѐнные в данной работе с использованием различных способов расчѐтов и применением различных пакетов инженерных и математических программ, таких как MathCAD и MatLab, являются неотъемлемой частью работы инженера и позволяют освоить, углубить и закрепить знания. Литература 1. Бесекерский В.А. Теория систем автоматического регулирования / В.А. Бесекерский, Е.П. Попов. – Л.: Профессия, 2003. – 751 с. 2. Мирошник, И. В. Теория автоматического управления. Линейные системы: Учеб. пособие для вузов / И.В. Мирошник. - М.: Питер, 2005.- 333 с. 3. Ерофеев, А. А.Теория автоматического управления: учебник для вузов / А. А. Ерофеев. - 2-е изд., доп. и перераб. - СПб.: Политехника, 2005. - 302 с. 4. Востриков, А. С. Теория автоматического регулирования: Учеб. пособие для вузов / А.С. Востриков, Г.А. Французова; Новосиб. гос. техн. ун-т. - Новосибирск: Изд-во НГТУ, 2003. - 363 с. 5. Ким, Д.П. Теория автоматического управления: учеб. пособие для студентов вузов / Д. П. Ким. - М.: Физматлит, 2003 - Т. 1: Линейные системы. - 2003. - 287 с. |