Интеллектуальный анализ данных Отчет ЛР 5. Задание 1 2 Теория 2 Ход работы 2 Вывод 4 Задание 2 5 Теория 5 Ход работы 5
 Скачать 387.51 Kb. Скачать 387.51 Kb.
|
Оглавление:Задание 1 2 Теория 2 Ход работы 2 Вывод 4 Задание 2 5 Теория 5 Ход работы 5 Задание 3 7 Теория 7 Ход работы 7 Вывод 8 Задание 4 9 Теория 9 Ход работы 10 Вывод 11 Задание 1Сгенерируйте вектор длины N=1000, элементами которого являются реализации нормально распределенной случайной величины с математическим ожиданием, равным 1, и стандартным отклонением, равным 0.3. Подсчитайте статистическое мат. ожидание и стандартную ошибку, не используя встроенные функции и проверьте правильность результата. Подсчитайте .95, .99-квантили. Исследуйте отклонение статистического мат. ожидания от 1 при росте N (N=1000,2000,4000,8000). ТеорияСлучайная величина x называется распределенной по нормальному (Гауссовскому) закону с параметрами α и σ (σ>0), если плотность распределения вероятностей имеет вид: 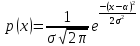 Нормальное распределение зависит от двух параметров — смещения и масштаба, то есть является с математической точки зрения не одним распределением, а целым их семейством. Значения параметров соответствуют значениям среднего (математического ожидания) и разброса (стандартного отклонения). Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1. Параметр математического ожидания определяет положение центра плотности вероятности нормального распределения. Параметр стандартного отклонения определяет разброс относительно центра. Оно рассчитывается как квадратный корень из дисперсии случайной величины: 𝜎=√𝐷|𝑋|. Дисперсия случайной величины — мера разброса данной случайной величины, т. е. её отклонения от математического ожидания. Пусть X— случайная величина, определённая на некотором вероятностном пространстве. Тогда 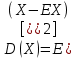 , где символ E обозначает математическое ожидание. , где символ E обозначает математическое ожидание.Квантиль в математической статистике — значение, которое заданная случайная величина не превышает с фиксированной вероятностью. Ход работыСоздадим вектор нормального распределения х с длиной N, равной 1000, с математическим ожиданием, равным 1, и стандартным отклонением, равным 0.3, с помощью встроенной в R функции rnorm, затем выведем вектор х (Рис. 1).  Рис. 1 – Создание вектора нормального распределения Подсчитаем математическое ожидание путем деления суммы всех элементов вектора на его длину. Сумму посчитаем стандартной функцией sum, которая складывает все элементы в векторе, выведем результат в консоль. Далее воспользуемся стандартной функцией подсчета математического ожидания mean для проверки полученного результата (Рис. 2).  Рис. 2 – Подсчет математического ожидания Подсчитаем стандартную ошибку путем деления стандартного отклонения на квадратный корень длины вектора. Найдем стандартной отклонение с помощью встроенной в R функции sd. (Рис. 3) Рис. 3 – Подсчет стандартной ошибки Подсчитаем .95, .99-квантили с помощью стандартной функциейquantileи выводим их с помощью функции print. (Рис. 4)  Рис. 4 – Подсчет .95, .99-квантилей Для исследования отклонения математического ожидания вектора от 1 при длине N (1000, 2000, 4000, 8000). Для этого создадим цикл, в котором будут векторы разной длины и вычисляем для каждого математическое ожидание, стандартное отклонение и отклонение математического ожидания от единицы. (Рис. 5)  Рис. 5 – Исследование отклонений математического ожидания Далее для наглядности построим график отклонения математического ожидания. (Рис. 6)  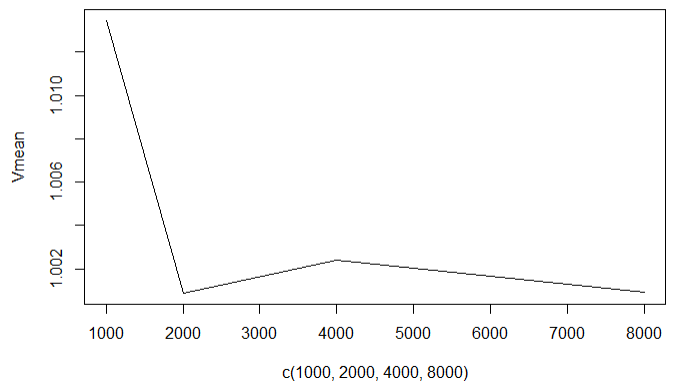 Рис. 6 – График отклонения математического ожидания ВыводПри увеличении длины вектора величина отклонения уменьшается, стремясь к 0. Следовательно, при длине вектора, стремящемся к бесконечности, математическое ожидание будет стремиться к математическому ожиданию генеральной совокупности. Задание 2Создайте фрейм данных из N=20 записей со следующими полями: Nrow — номер записи, Name — имя пользователя, BirthYear — год рождения, EmployYear — год приема на работу, Salary — зарплата, где Nrow изменяется от 1 до N, Name задается произвольно, BithYear распределен равномерно на отрезке [1960,1985], EmployYear распределен равномерно на отрезке [BirthYear+18,2006], Salary для работников младше 1975 г.р. определяется по формуле Salary=(ln(2007-EmployYear)+1)*8000, для остальных Salary=(log2(2007-EmployYear)+1)*8000. Подсчитайте число сотрудников с зарплатой, большей 15000. Добавьте в таблицу поле, соответствующее суммарному подоходному налогу (ставка 13%), выплаченному сотрудником за время работы в организации, если его зарплата за каждый код начислялась согласно формулам для Salary, где вместо 2007 следует последовательно подставить каждый год работы сотрудника в организации. ТеорияФрейм данных (dataframe) – это самая мощная встроенная структура данных языка R, напоминающая табличную матрицу, в которой каждый столбец имеет одинаковую длину и должен иметь имя. Каждый столбец фрейма данных обрабатывается так, как если бы он был элементом структуры данных список. Мы используем функцию data.frame для построения объекта фрейма данных из векторов и факторов. Характеристики фрейма данных: Имена столбцов должны быть непустыми. Имена строк должны быть уникальными. Данные, хранящиеся во фрейме данных, могут быть числовыми, факторными или символьными. Каждый столбец должен содержать одинаковое количество элементов данных. Ход работыОбъявляем переменные, объявляем функцию подсчета зарплаты в зависимости от года рождения сотрудника, объявляем список сотрудников, состоящий из 20 записей (Рис. 7) 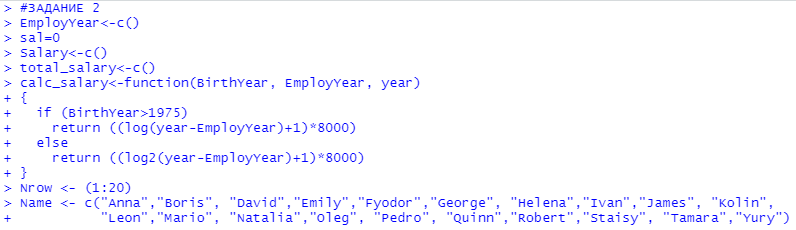 Рис. 7 – Объявление полей и функции подсчета зарплаты Далее в циклах рассчитываем год трудоустройства, зарплату, исходя из года рождения сотрудника, подсчитываем и выводим число сотрудников с зарплатой больше 15000 (их 17) (Рис. 8). 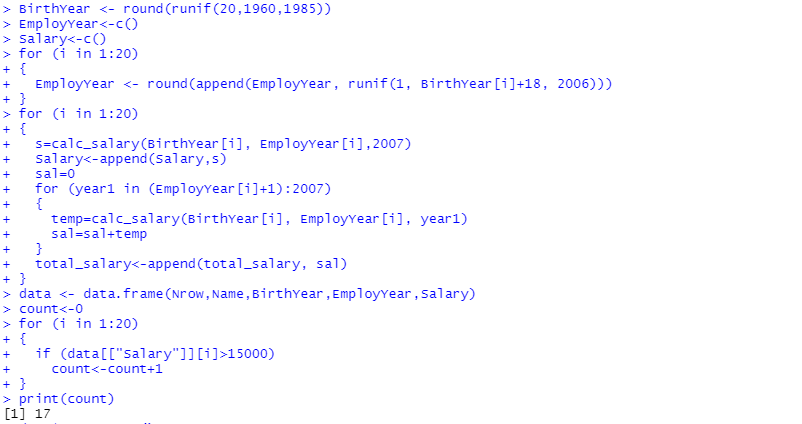 Рис. 8 – Полученные данные Далее выводим на экран все поля, включая поле, соответствующее суммарному подоходному налогу, выплаченному сотрудником за время работы в организации (Рис. 9)  Рис. 9 – Вывод результата И получаем результат (Рис. 10) 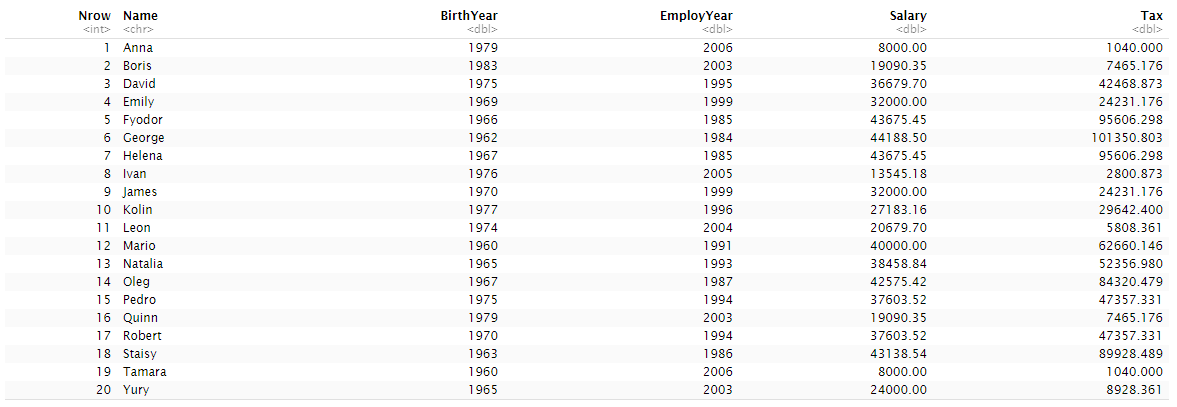 Рис. 10 – Результат Задание 3Напишите функцию, которая принимает на вход числовой вектор x и число разбиений интервала k (по умолчанию равное числу элементов вектора, разделенному на 10) и выполняет следующее: находит минимальное и максимальное значение элементов вектора xmin и xmax, разделяет полученный отрезок [xmin;xmax] на k равных интервалов и подсчитывает число элементов вектора, принадлежащих каждому интервалу. Далее должен строиться график, где по оси абсцисс — середины интервалов, по оси ординат — число элементов вектора, принадлежащих интервалу, разделенное на общее число точек. Проведите эксперимент на данной функции, где x — вектор длины 5000, сгенерированный из экспоненциально распределенной случайной величины, k=500. Приближение какого графика мы получаем в итоге при большом числе точек и числе разбиений? ТеорияПлотность распределения величины X с экспоненциальным законом распределения задается формулой: 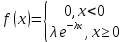 Функция распределения величины X: 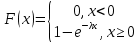 λ – параметр данного распределения, полностью определяющий его свойства. В частности, числовые характеристики выражаются через этот параметр: M(X)=1/λ, M(X)=1/λ, D(X)=1/λ2D(X)=1/λ2. Ход работыСоздадим функцию f, которая принимает на вход числовой вектор x и число разбиений интервала k, которое по умолчанию равняется числу элементов вектора, поделенному на 10, в переменные xmin и xmax записываем соответственно минимальное и максимальное значения вектора х. Отрезок от xmin и xmax разделяем на k равных интервалов. Здесь же объявляем массивы middle и num_el_int, в которые будем класть середины интервалов и число элементов вектора, принадлежащие интервалу (Рис. 11)  Рис. 11 – Объявление функций Далее создадим цикл от 1 до k, в котором заполняем массивы middle и num_el_int, находим число элементов вектора, разделенное на общее число точек, создаем график, где по оси абсцисс выводятся середины интервалов, а по оси ординат – количество элементов вектора, принадлежащих данному интервалу (Рис. 12)  Рис. 12 – Заполнение массивов и графиков Применим функцию f, которая принимает на вход числовой вектор, сгенерированный из экспоненциально распределенной случайной величины с помощью функции rexp, принимающей значения 5000 и 0.3, и получим график результата (Рис. 7) 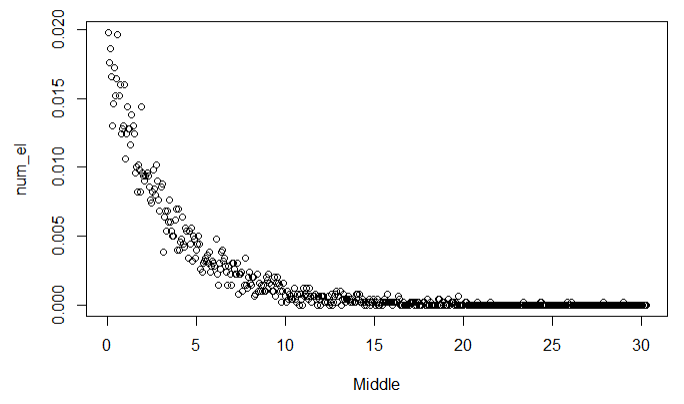 Рис. 7 – График функции func(rexp(5000, 0.3)) Применим ту же функцию, указав число разбиений интервала k, равное 50. (Рис. 8) 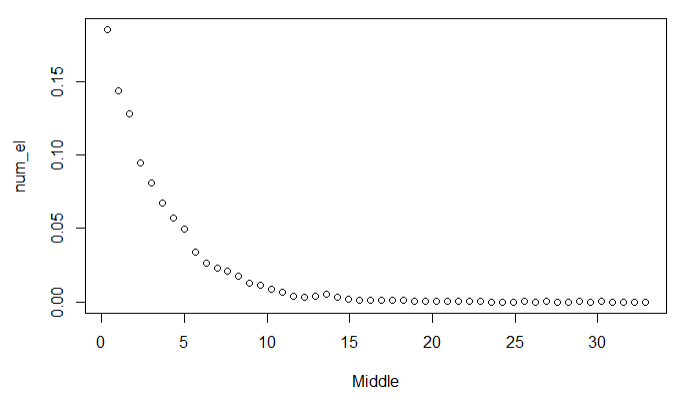 Рис. 8 – График функции func(rexp(5000, 0.3), 50) ВыводПри большом числе разбиений график приближается к графику плотности экспоненциального распределения. Задание 4Спроектируйте и реализуйте метод наименьших квадратов. ТеорияМетод наименьших квадратов — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных. Он может использоваться для «решения» переопределенных систем уравнений (когда количество уравнений превышает количество неизвестных), для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функции. МНК является одним из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным. Пусть экспериментальные данные надо представить линейной функцией y=ax+b. Требуется подобрать такие значения 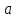 и и 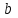 , для которых функция , для которых функция будет минимальной. Необходимые условия минимума функции сводятся к системе уравнений:  После преобразований получаем систему двух линейных уравнений с двумя неизвестными:  Решив ее, находим искомые значения параметров  и и 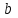 Определяем значение параметров: 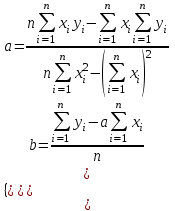 Для вычисления коэффициентов необходимо найти следующие составляющие: 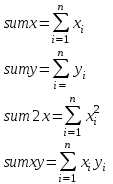 Тогда значение параметры будут определены как: 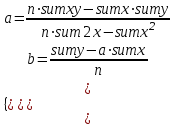 Ход работыСоздадим функцию mnk, которая принимает на вход векторы x и у, а затем реализует метод наименьших квадратов, объявим переменные, заполним их значения в цикле (Рис. 15)  Рис. 15 – Объявление и заполнение переменных Посчитаем коэффициенты a и b по методу наименьших квадратов и выведем график (Рис. 16) 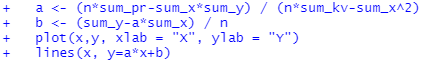 Рис. 16 – Подсчет коэффициентов Метод наименьших квадратов подходит для работы с любыми данными, но для наглядной демонстрации выберем такой набор данных: массив Х – площадь квартиры в Уфе в квадратных метрах, массив Y – цена квартиры в сотнях тысяч рублей. Применим созданную функцию (Рис. 17) 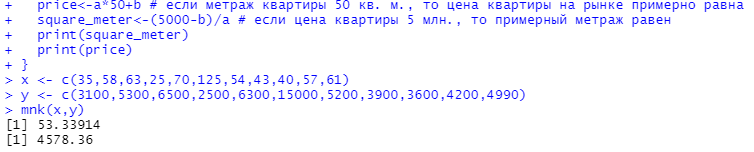 Рис. 17 – Применение МНК Если стоимость квартиры равна 5 млн., то примерный ее метраж будет равен 53 кв.м. Если метраж квартиры 50 кв.м., то примерная цена будет равна 4.6 млн. Получаем график (Рис. 18) 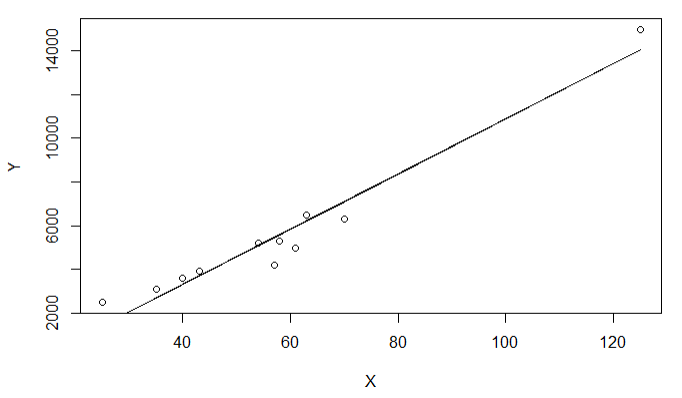 Рис. 18 – График функции метода наименьших квадратов. ВыводУравнение обозначает линейную связь между метражом квартиры и ее ценой. Подставив коэффициенты, полученные методом МНК, можно спрогнозировать стоимость жилья. Значения данных (точки на прямой) находятся близко к прямой регрессионного уравнения, следовательно, коэффициенты найдены верно. Уравнение регрессии имеет вид: y = 126.272*x -1735.242 |
