Бабенко Задание на контрольную работу СЦОС. Задание на контрольную работу (Бабенко)
 Скачать 1.12 Mb. Скачать 1.12 Mb.
|
Задание на контрольную работу (Бабенко)Выбор вариантов заданий производится студентом из соответствующих таблиц по последним цифрам номера его зачетной книжки. Задания 1 и 2 требуют от студента изложения теоретического материала по разделам дисциплины согласно номеру индивидуального варианта, определяемого из приведенных ниже таблиц по последней цифре номера зачетной книжки студента (задание 1) и предпоследней цифре зачетной книжки (задание 2). Задания 3 и 4 требуют осуществить разработку кодов. ЗАДАНИЕ 1. Раскрыть суть приведенных в таблице 2 понятий, средств и технологий. Таблица 2 - Варианты индивидуальных заданий
ЗАДАНИЕ 2. Раскрыть суть приведенных в таблице 3 понятий, средств и технологий. Таблица 3 - Варианты индивидуальных заданий
Задание 3. Провести кодирование алфавита (по варианту) по алгоритму Хаффмена. Алгоритм Хаффмена а) Располагаем символы алфавита в порядке убывания вероятностей
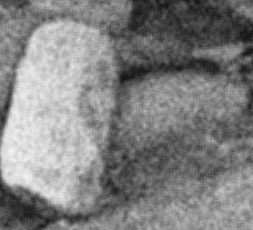
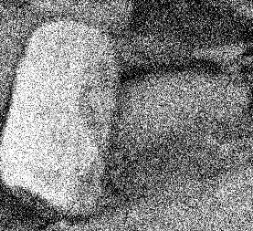
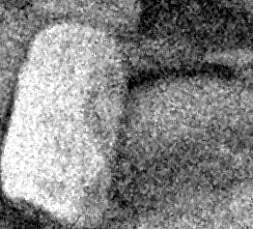
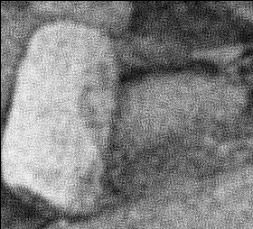
Строим дерево Хаффмена. Откладываем вправо большую вероятность, 1 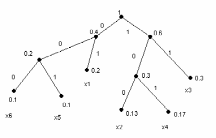 Этот код является префиксным 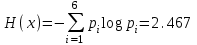 бит бит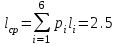 Коэффициент эффективности кода 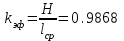 Этот код является однозначным 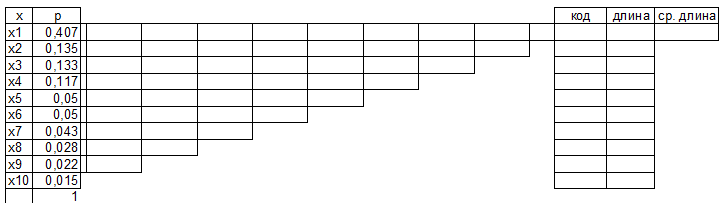 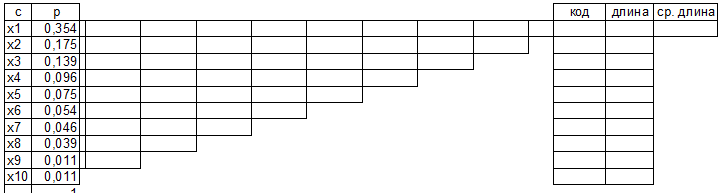 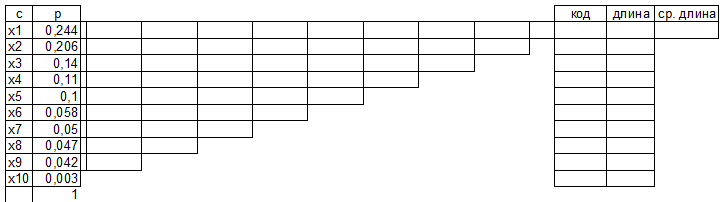 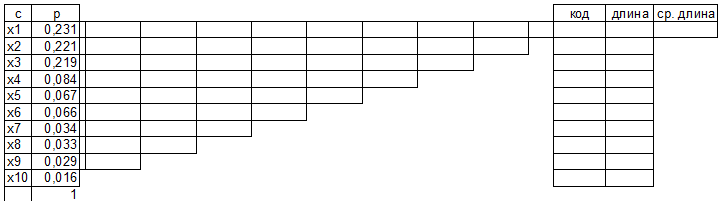 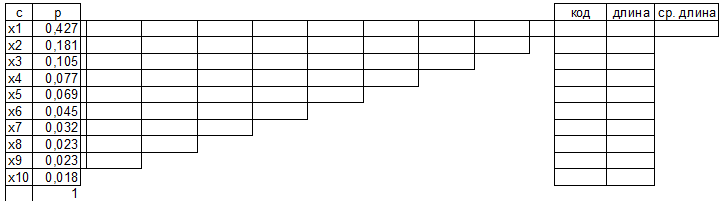 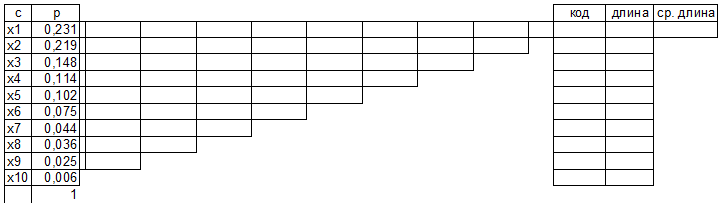 Задание 4. Изучить методы фильтрации изображений. Для метода по варианту составить алгоритм фильтрации. Привести пример для изображения 10х10 с подробным описанием (изображение удобнее представить в виде таблицы, каждый элемент которой представляет собой уровень яркости). 1 Метод среднего (локальное усреднение в области точки) Для фильтрации используется окно размерами (2n + )·(2n + 1). В качестве оценки уровня яркости в средней точке окна используется формула: 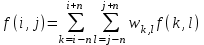 , ,где 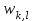 – весовые коэффициенты. – весовые коэффициенты.Возможны два варианта формирования весовых коэффициентов: а) в пределах окна все веса одинаковые: 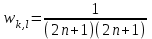 ; ;б) веса убывают от центра окна к краям. Но при этом должно выполняться условие нормировки: 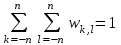 . .2 Метод сглаживания по обратному градиенту Суть метода заключается в следующем: чем меньше разность 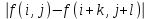 , тем меньше должно быть значение веса , тем меньше должно быть значение веса 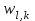 . В данном методе точки сглаженного изображения будут вычисляться по формуле: . В данном методе точки сглаженного изображения будут вычисляться по формуле: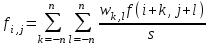 , ,где веса: 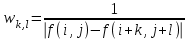 , если , если 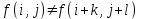 , ,или 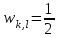 , если , если 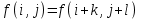 . .Масштабирующий коэффициент 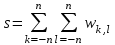 . .Для этого метода для каждого окна вычисляются свои веса. 3 Метод s-фильтра Метод основан на полном исключении вклада точек, не удовлетворяющих некоторой модели однородности. Предполагается гауссовский тип распределения. В данном методе точки сглаженного изображения будут вычисляться по формуле: 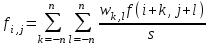 , ,где 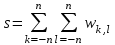 ; ;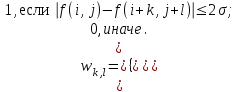 Значение s вычисляется на некоторой однородной области изображения (в простейшем случае – на всем изображении): 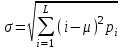 ; ;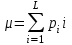 , ,где L – количество уровней яркости (в нашем случае 256), pi – вероятность появления на изображении точки с яркостью i-го уровня. 4 Метод усреднения по К ближайшим соседям Среди всех точек окна выбирается множество точек G мощностью 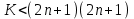 , таких, что , таких, что 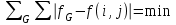 . .Тогда точки сглаженного изображения будут вычисляться по формуле: 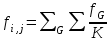 . .5 Сглаживание по наиболее однородной окрестности центральной точки Для большого (исходного) окна 5x5 имеем 9 меньших окон 3x3 (рис. 1). Для каждого меньшего окна вычисляется величина 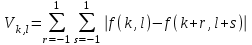 . .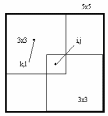 Рисунок 1 – Принцип формирования меньших окон Это суммарное отклонение яркости точек малого окна от яркости его центральной точки. Затем выбирается окно с минимальным отклонением и по нему сглаживается исходная точка с координатами i, j. 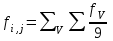 . .6 Медианный фильтр Используют окно 3x3. При больших размерах окна возможны потери. Из девяти значения яркости окна выбирают такое 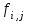 , что , что 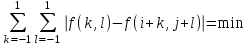 , ,то есть центральной точке окна присваивается яркость точки, имеющей минимально отличающуюся от нее яркость. На рисунке 2 показаны результаты обработки изображения различными методами фильтрации.
Рисунок 2 – Результаты обработки изображения различными методами фильтрации . Список литературы1 Сергиенко А. Б. Цифровая обработка сигналов: учеб. пособие. — 3-е изд. — СПб.: БХВ-Петербург, 2011. — 768 с. - (ЭБС "znanium.com"). - Режим доступа: http://znanium.com/catalog.php?bookinfo=354905 2 Сажнев А. М., Микушин, А. В. Цифровые устройства и микропроцессоры: учеб. пособие / А. В. Микушин, А. М. Сажнев, В. И. Сединин. — СПб.: БХВ-Петербург, 2010. — 832 с. - Режим доступа: http://znanium.com/catalog.php?bookinfo=350706 3 Гуров В.В. Архитектура микропроцессоров: учеб. пособие / В. В. Гуров. - М. : Интернет-Ун-т Информ. Технологий; БИНОМ. Лаб. знаний, 2012. - 272 с. 4 Кангин В.В. Аппаратные и программные системы управления. Промышленные сети и контроллеры : учеб. пособие для вузов / В. В. Кангин, В. Н. Козлов. - М : БИНОМ. Лаб. знаний, 2010. - 418 с. 5 Федосов, В. П. Цифровая обработка сигналов в LabVIEW [Электронный ресурс] : учеб. пособие / В. П. Федосов, А. К. Нестеренко; под ред. В. П. Федосова. - М.: ДМК Пресс, 2009. - 456 с. - Режим доступа: http://znanium.com/catalog.php?bookinfo=409323 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||