Закон движения материальной точки. Траектория. Вектор перемещения. Путь
 Скачать 0.72 Mb. Скачать 0.72 Mb.
|
Молярная теплоемкость: | 27. Обратимые и необратимые процессы и циклы. Примеры таких процессов. Тепловая машина и ее КПД. Холодильная машина. Цикл Карно и его КПД. Термодинамический процесс, совершаемый системой, наз. обратимым, если он может быть проведен в прямом и обратном направлениях через те же состояния (но в обратной последовательности) так, что после осуществления прямого и обратного процесса в окружающей среде не возникаем никаких остаточных изменений. Примеры:
Для осуществления превращения теплоты, переданной системе, в работу созданы специальные устройства – тепловые машины. Цель действия тепловой машины – получение работы А, которую над внешними телами будет совершать рабочее тело. Для совершения рабочим тело работы ему передается некоторое количество теплоты Мерой эффективноти преобразования теплоты, подведенной к рабочему телу, в работу тепловой машины над внешними телами является КПД, который равен отношению работы, совершенной рабочим телом за один цикл, к количеству теплоты, полученному рабочим телом от нагревателя в этом цикле: 1-2, 3-4 – изотермы, 2-3, 4-1 – адиабаты. КПД цикла Карно будет максимальным среди КПД всех возможных циклов, которые рабочее тело может осуществить между нагревателем и холодильником с заданными температурами 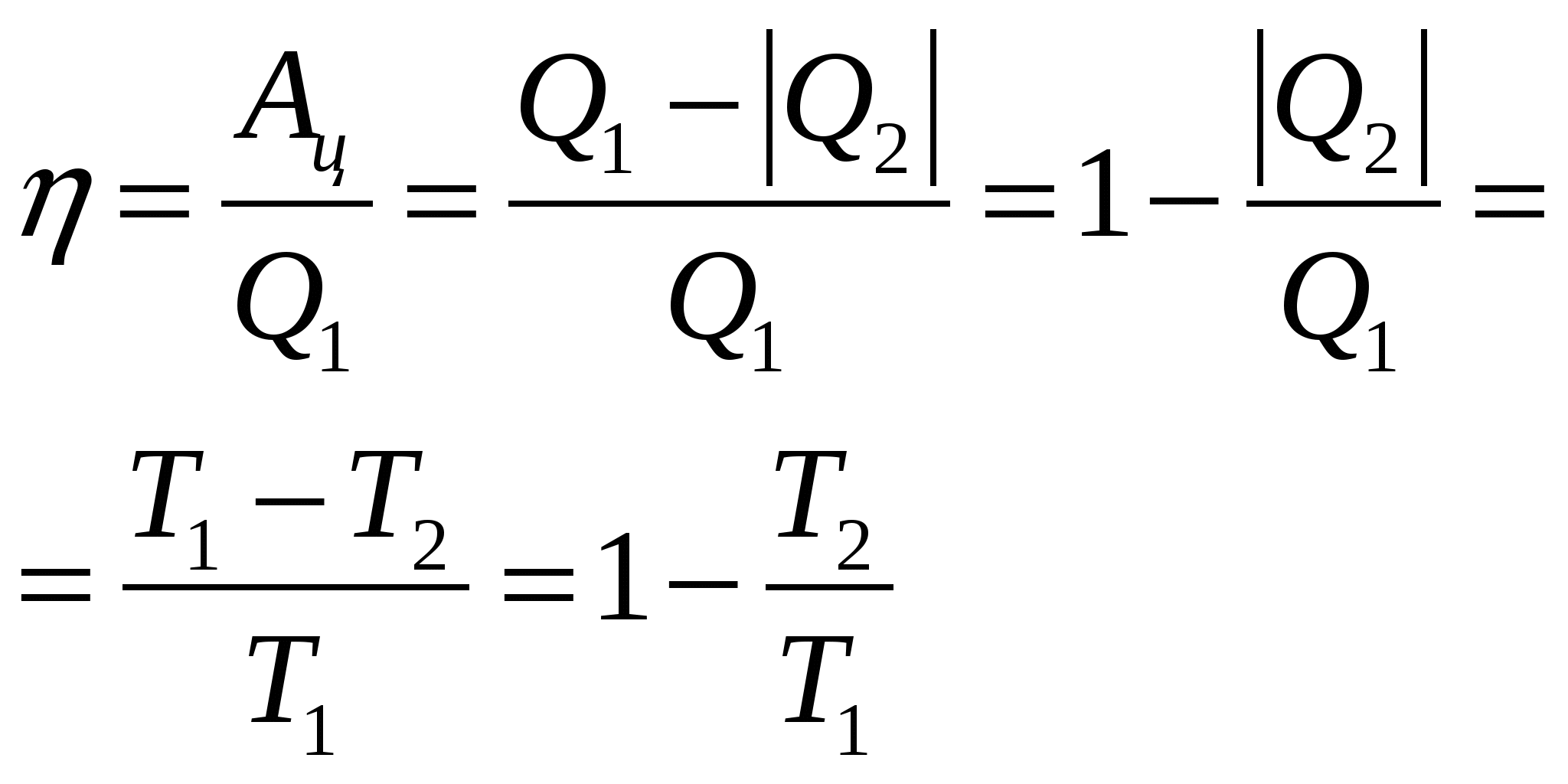 Тепловая машина, работающая по циклу Карно, наз. идеальной тепловой машиной. Тепловая машина, работающая по циклу Карно, наз. идеальной тепловой машиной. | ||||||
| 28. Цикл Карно, КПД цикла Карно. Второе начало термодинамики. Его различные формулировки. Цикл Карно: 1-2, 3-4 – изотермы, 2-3, 4-1 – адиабаты. КПД цикла Карно будет максимальным среди КПД всех возможных циклов, которые рабочее тело может осуществить между нагревателем и холодильником с заданными температурами 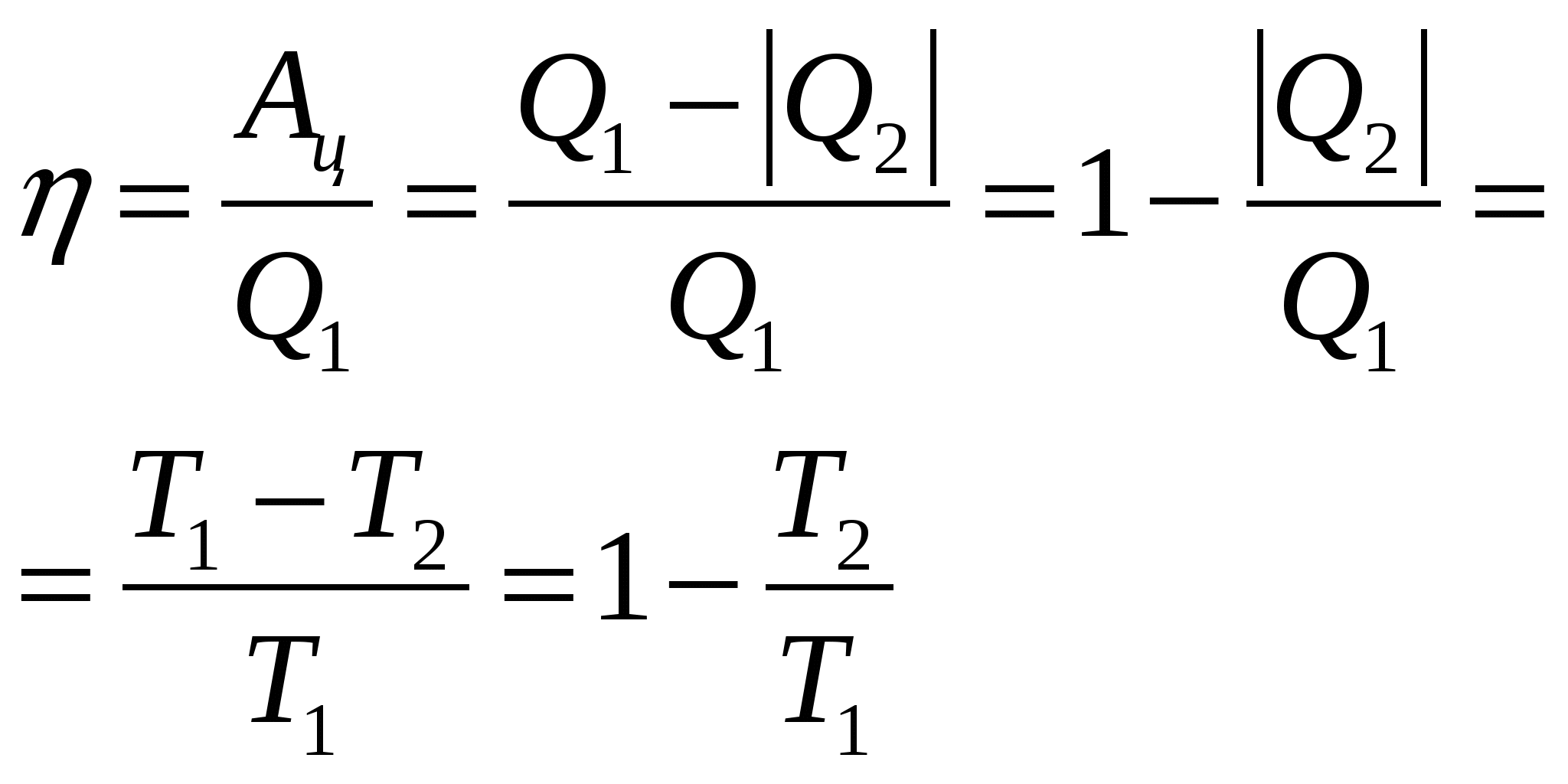 Тепловая машина, работающая по циклу Карно, наз. идеальной тепловой машиной. Тепловая машина, работающая по циклу Карно, наз. идеальной тепловой машиной.Второе начало термодинамики:
| 29. Энтропия – функция состояния термодинамической системы. Основное свойство энтропии (формулировка второго начала термодинамики через энтропию). Статистический смысл второго начала. Каждому состоянию газа соответствует некоторое распределение его молекул по объему и определенное распределение молекул по скоростям. В целом вероятность какого-либо состояния системы W больше вероятности w отдельного распределения в Р раз: W = wP, где Р – термодинамическая вероятность состояния системы. Она равна числу всевозможных микрораспределений частиц по координатам и скоростям, соответствующих данному термодинамическому состоянию (макросостоянию). W≤1, w≤1, Р≥ 1. Статистическое толкование второго закона термодинамики: Энтропия изолированной системы не убывает: термодинамическая вероятность состояния изолированной системы не может убывать. | 30. Понятие эффективного диаметра молекулы и эффективного сечения процесса столкновений. Число столкновений одной молекулы газа в единицу времени. Средняя длина свободного пробега молекулы и ее зависимость от давления и температуры. Эффективный диаметр – среднее расстояние между центрами молекул, на которое две молекулы сближаются при их столкновении. Площадь поперечного сечения «коридора», в который должны попасть центры соседних молекул, чтобы столкнуться с данной, наз. эффективным сечением столкновения: Число столкновения молекул за единицу времени: Средняя длина свободного пробега молекулы – расстояние которое она пролетает между двумя последовательными соударениями: С учетом движения всех молекул, заменяя среднюю скорость на относительную скорость движения молекул: Так как p = nkT, то | |||||
| 31. Явления переноса в газах. Опытные законы диффузии, теплопроводности и вязкости. Качественное и количественное описание этих процессов в молекулярно-кинетической теории газов. Явления, происходящие пр нарушении равновесного состояния систем, наз. явлениями переноса (например, столкновения молекул, диффузия, теплопроводность, вязкость). Неравновесный процесс, вызываемый молекулярным тепловым движением и приводящий к установлению равновесного распределения концентраций путем взаимопроникновения и перемешивания молекул, наз. диффузией. Диффузия – это перенос массы. Назовем плотностью потока молекул их число, проходящее через единичное сечение, расположенное перпендикулярно вектору скорости, за единицу времени: Коэффициент диффузии: Закон диффузии (закон Фика): Плотность диффузионного потока частиц пропорциональная градиенту концентрации частиц. При диффузии поток частиц направлен в сторону их концентрации (смысл знака «-»). Молекулярный перенос теплоты в сплошной среде, обусловленный наличием градиента температуры, называется теплопроводностью. Плотность теплового потока (количество теплоты, проходящее через единичную поверхность за единицу времени): Плотность потока частиц: Коэффициент теплопроводности: Закон теплопроводности (закон Фурье): Свойство жидкостей и газов, характеризующее сопротивление действию внешних сил, вызывающих их течение, наз. вязкостью (внутренним трением). Можно рассматривать вязкость как перенос импульса. Плотность потока импульса: Закон внутреннего трения (закон Пуазейля): | 32. Барометрическая формула. Распределение Больцмана. Больцман получил барометрическую формулу – зависимость давления газа от высоты в потенциальном поле тяжести Земли. Рассмотрим равновесие некоторого объема (цилиндр высотой dh) газа, находящегося на высоте h от поверхности Земли, уровень которой выберем за условный ноль отсчета потенциальной энергии. Так как столбик газа находится в равновесии, 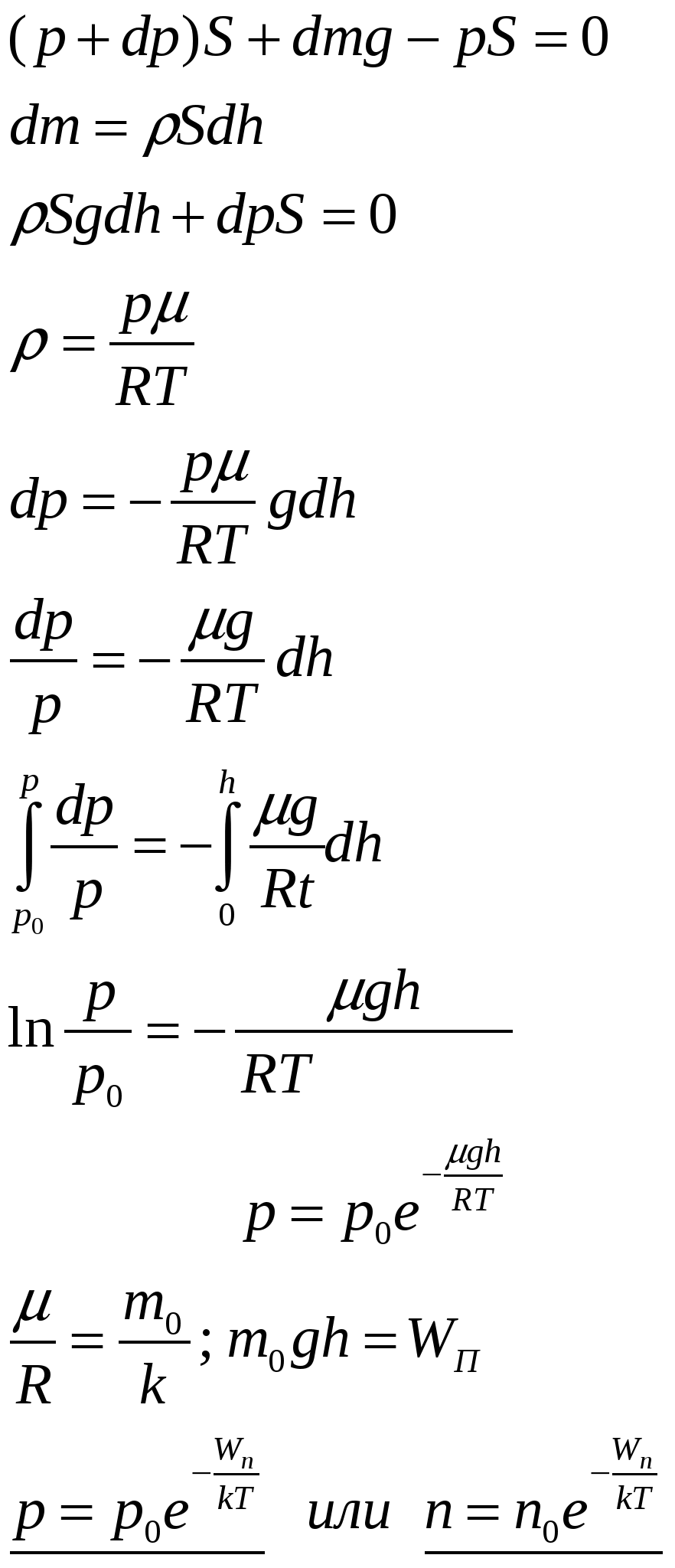 Энергия движения молекулы определяется, в свою очередь, энергией ее поступательного движения, энергией ее вращения и энергией колебания атомов в молекуле: Энергия движения молекулы определяется, в свою очередь, энергией ее поступательного движения, энергией ее вращения и энергией колебания атомов в молекуле:Минимальное число независимых переменных, однозначно определяющих положение тела в пространстве (или минимальное число независимых перемещений тела в пространстве) наз. числом степеней свободы ( i ) тела. Для одноатомной молекулы i = 3 Закон Больцмана о равномерном распределении энергии молекул по степеням свободы: если система молекул находится в тепловом равновесии при температуре Т, то средняя кинетическая энергия молекул равномерно распределена по степеням свободы, причем на каждую степень свободы приходится энергия | 33. Распределение молекул газа по скоростям (распределение Максвелла). Смысл функции распределения. Наиболее вероятная, средняя и средняя квадратичная скорости молекул. Зависимость функции распределения от температуры. Максвелловский закон распределения молекул газа по скоростям определяет, какое число dN молекул газа из общего числа его молекул N в единице объема имеет при данной температуре скорости, заключенные в интервале от v до v+dv: 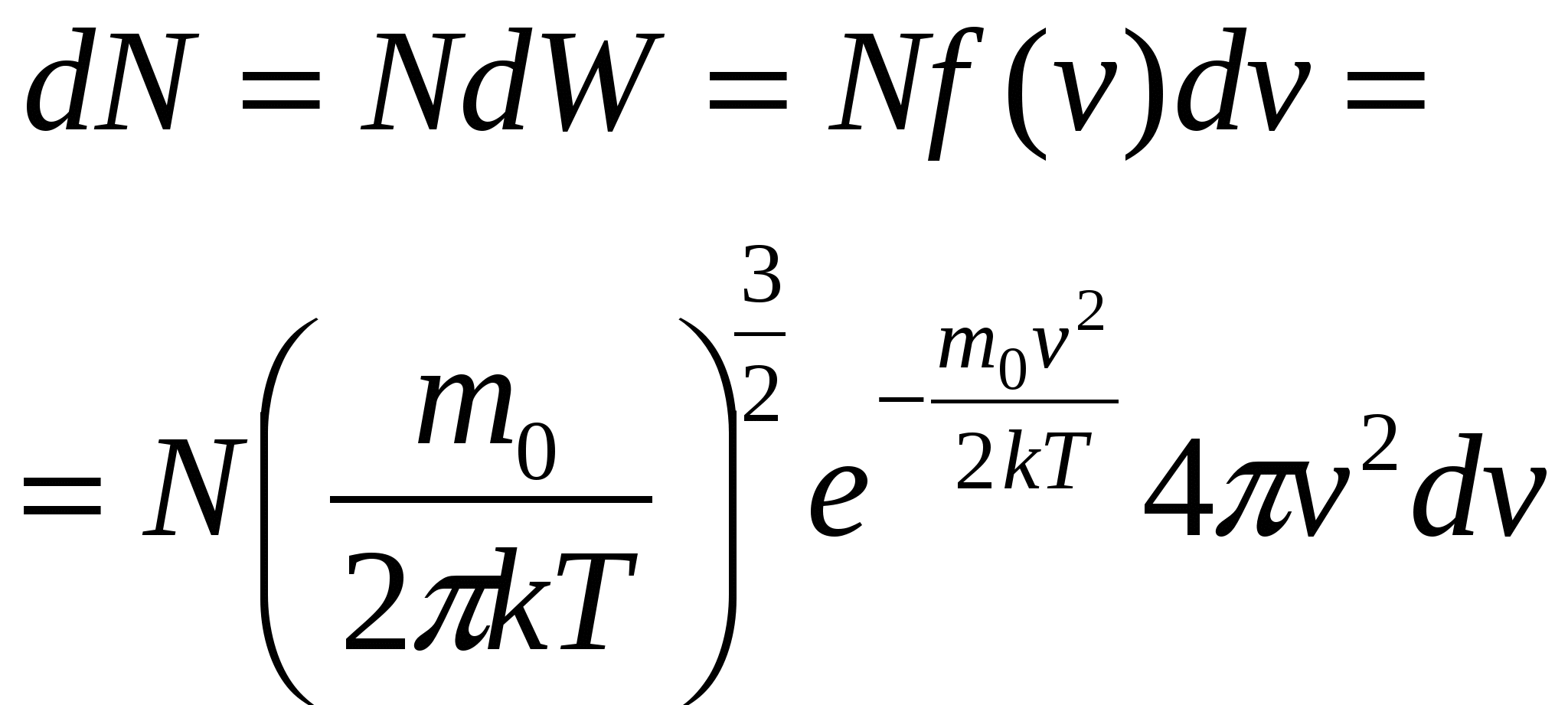 Проанализируем поведение функции распределения молекул по скоростям 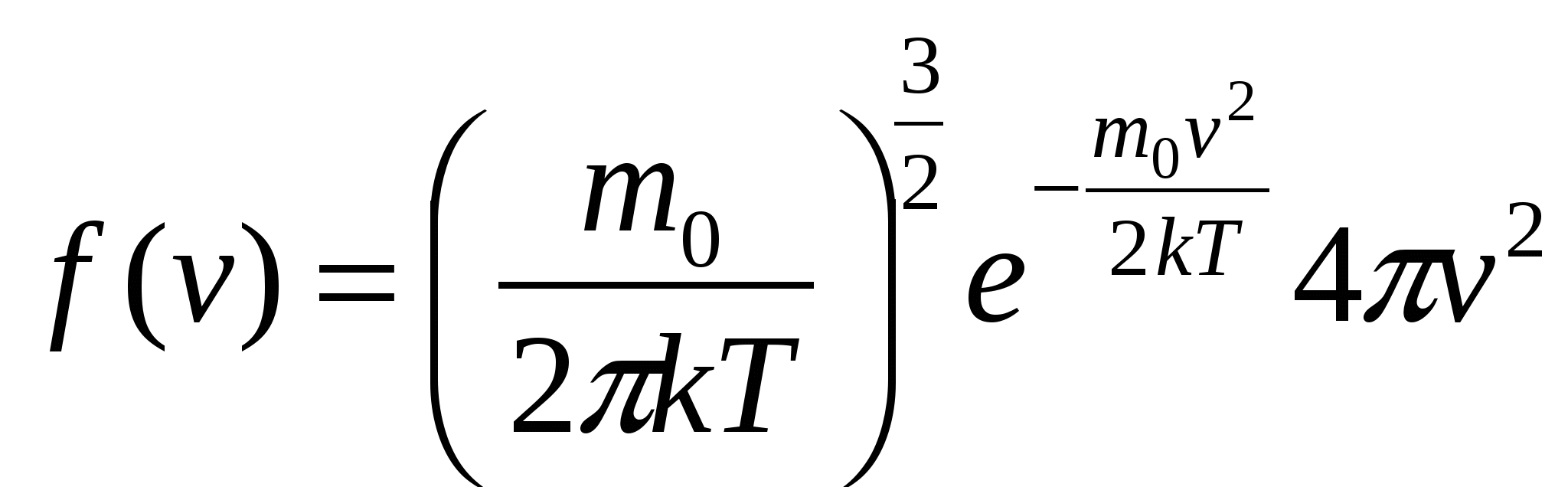 Найдем, при какой скорости наблюдается максимальное значение функции f(v). Такую скорость назовем наиболее вероятной скоростью молекул. Найдем, при какой скорости наблюдается максимальное значение функции f(v). Такую скорость назовем наиболее вероятной скоростью молекул. |
