|
|
Закон движения материальной точки. Траектория. Вектор перемещения. Путь
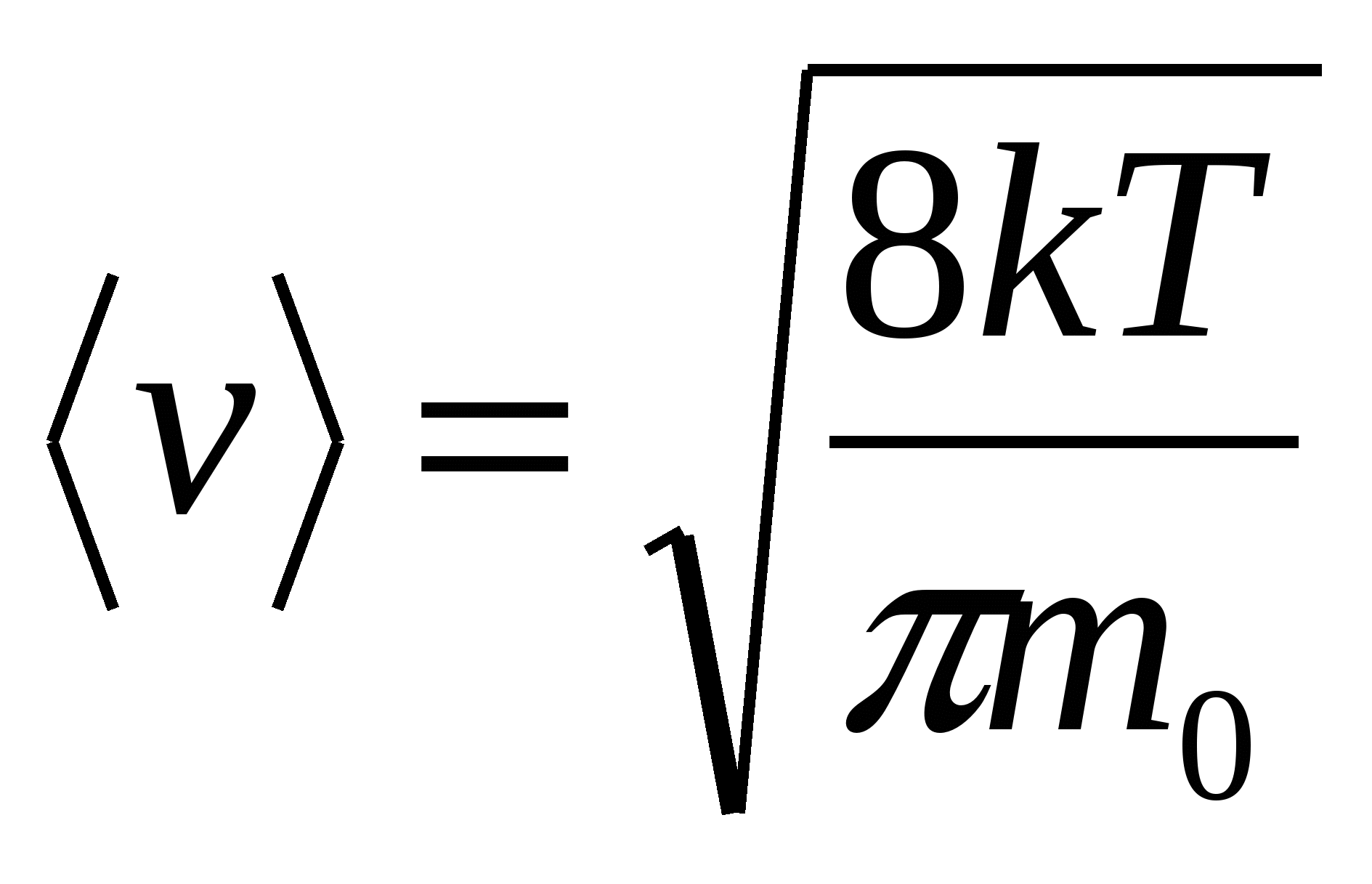
Средняя квадратичная скорость
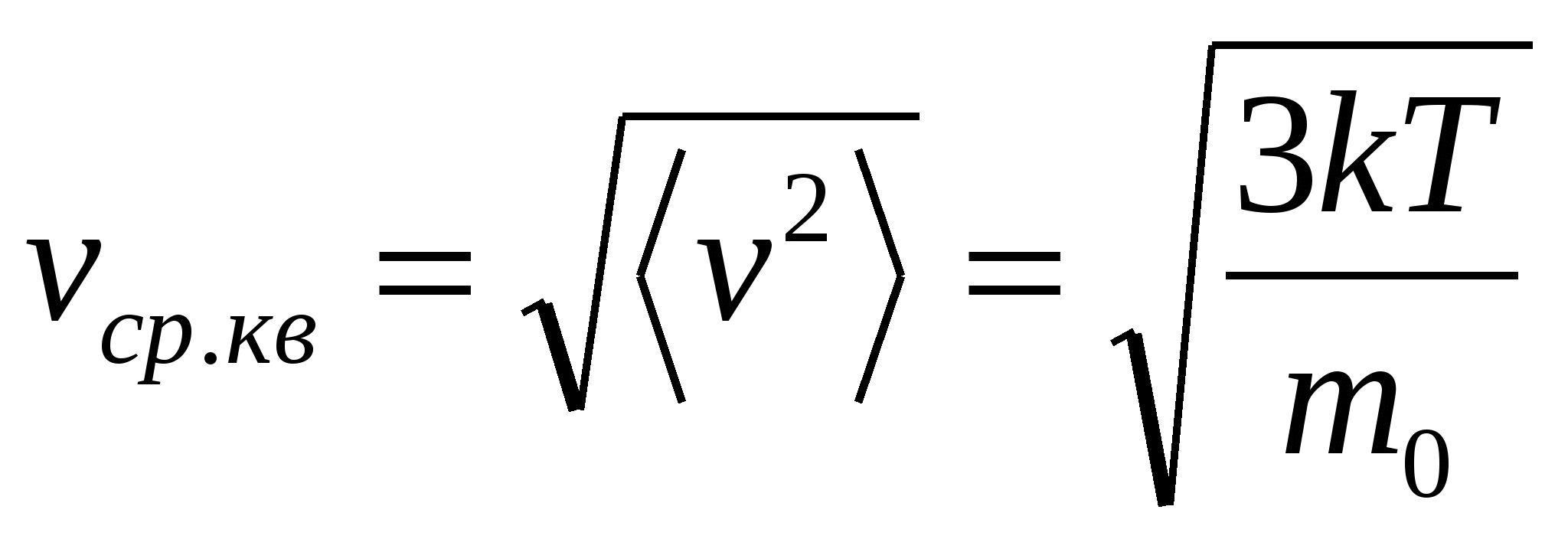
Функция распределения плотности вероятности позволяет найти не число молекул, скорости которых лежат в определенном интервале скоростей, а только долю от общего числа молекул.
Максвелловское распределение нельзя использовать для анализа систем молекул при очень высоких температурах. При таких температурах максимум кривой распределения резко «сдвигается» в область больших скоростей, и скорости молекул могут даже превысить скорость света.
Максвелловское распределение нельзя использовать для анализа систем молекул при очень низких температурах. При таких температурах максимум кривой распределения резко «сдвигается» в область малых скоростей, и кривая сильно сужается. Тогда в рассматриваемом интервале скоростей может оказаться очень мало молекул, следовательно, к такому числу частиц нельзя применять методы теории вероятностей.
34. Реальные газы. Уравнение Ван-дер-Ваальса. Изотермы реального газа (теоретические и экспериментальные). Критические параметры реального газа.
Свойства не сильно разреженных газов отличаются от свойств идеальных газов, подчиняющихся уравнению Клапейрона-Менделеева. Фактор сжимаемости  , теплоемкость, вязкость и другие свойства значительно отличаются от соответствующих свойств идеальных газов. Это связано с тем, что между молекулами газа действуют силы, которые в теории идеальных газов не принимаются во внимание. Во всех реальных телах молекулы взаимодействуют друг с другом. Силы взаимодействия между молекулами в сильной степени зависят от расстояния между ними. Эти силы имеют электромагнитную, а также особую квантовую природу.
В первом приближении молекулы реального газа можно уподобить твердым шарикам диаметром d, между которыми действуют только силы взаимного притяжения. Такая модель газа, принятая Ван-дер-Ваальсом, позволила ему получить уравнение состояния реального газа более совершенное, чем уравнение Клапейрона-Менделеева.
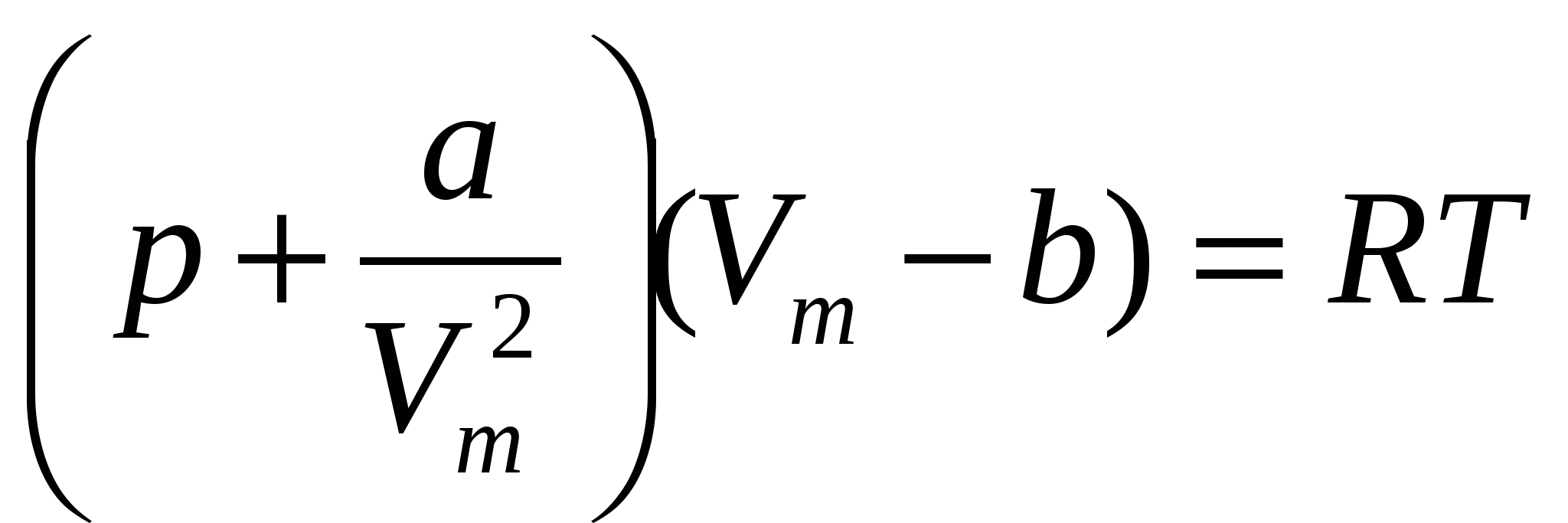
b – поправка Ван-дер-Ваальса, представляет собой запрещенный объем (центры других молекул, соударяющихся с данной, не могут находиться внутри этого объема, центр которого совпадает с центром произвольной молекулы), приходящийся на все NA молекул в моле газа: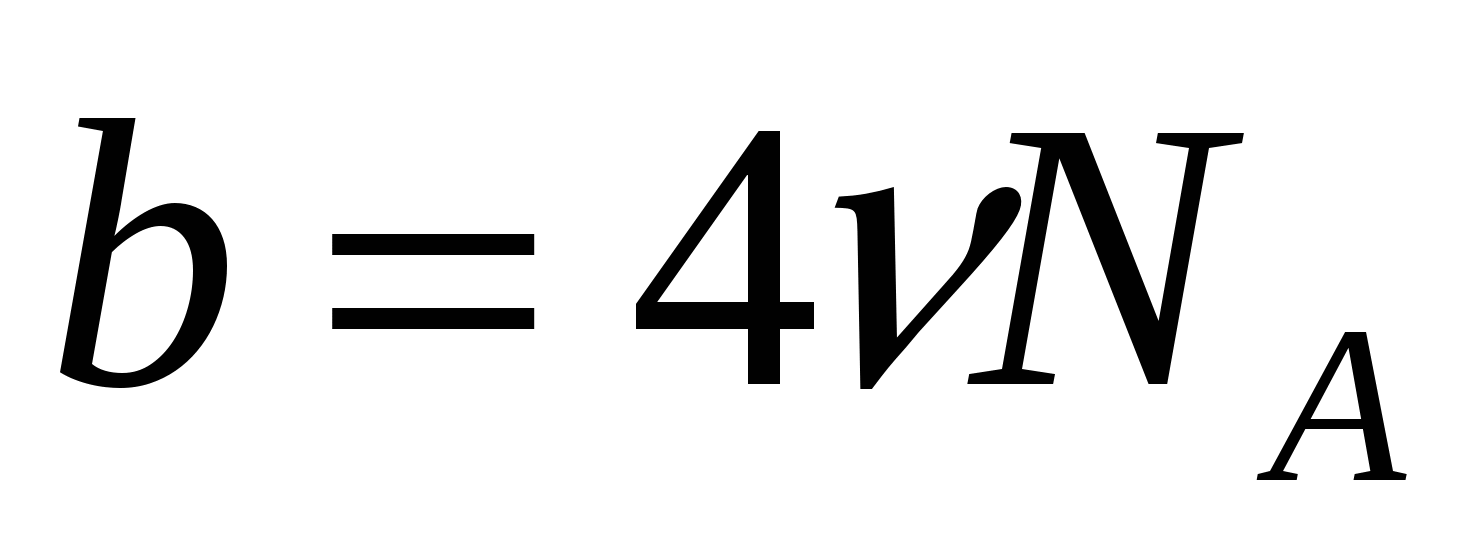
а - коэффициент пропорциональности (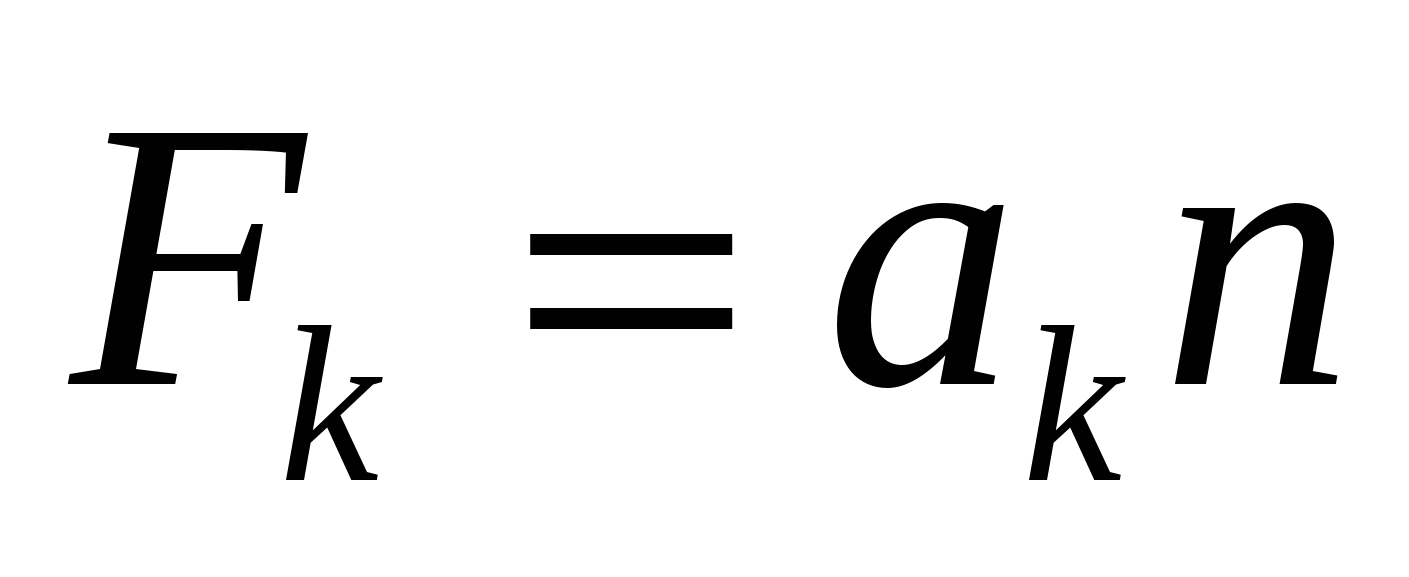 - сила притяжения молекулы пропорциональна концентрации молекул), коэффициент а зависит от химической природы газа и расстояния от центра молекулы до стенки сосуда.
Для произвольного числа молей реального газа:
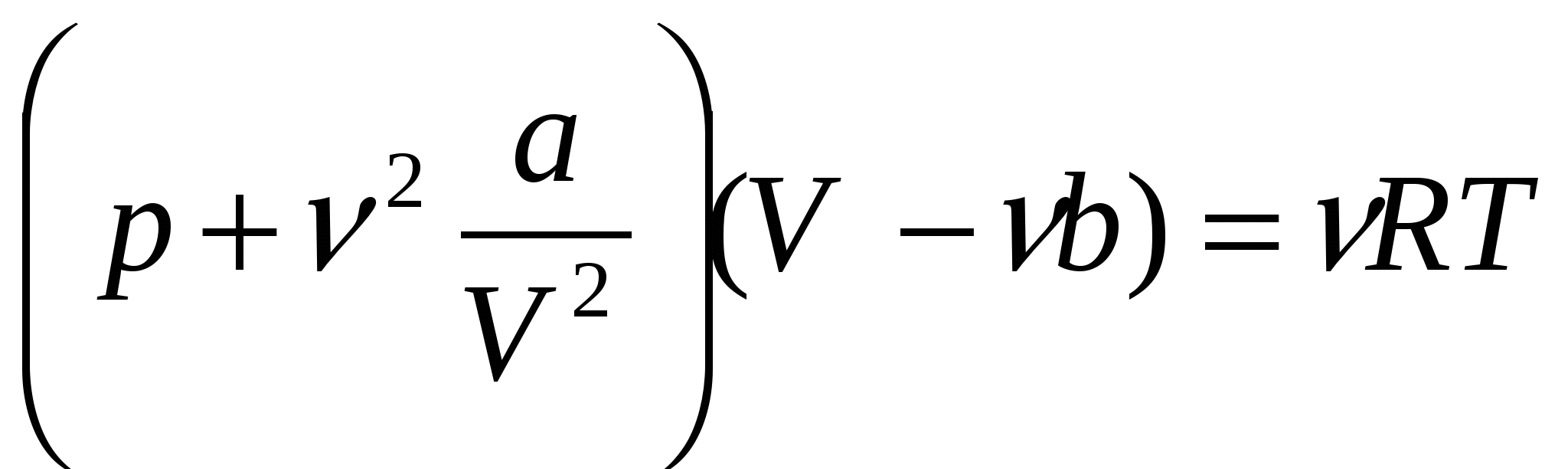
При температурах, меньших Ткр, на каждой изотерме имеется горизонтальных участок, на котором постоянна не только температура, но и давление, а молярный объем может принимать любые значения в некотором интервале от VB до VC. Разность VC- VB возрастает с понижением температуры. При увеличении температуры эта разность стремится к 0 при приближении температуры к значению Ткр, которое наз. критической температурой. Точки В и С сливаются в одну точку К – критическую точку – на изотерме, соответствующей критической температуре (критической изотерме). В – состояние кипящей жидкости, С – сухой насыщенный пар.
При приближении к критической точке исчезают различия между жидким и газообразным состояниями. В критическом состоянии обращаются в 0 разность молярных объемов кипящей жидкости и сухого насыщенного пара, удельная теплота парообразования и поверхностное натяжение жидкости.
BD – перегретая жидкость
CE – пересыщенный пар.
|
|
| |
|
|
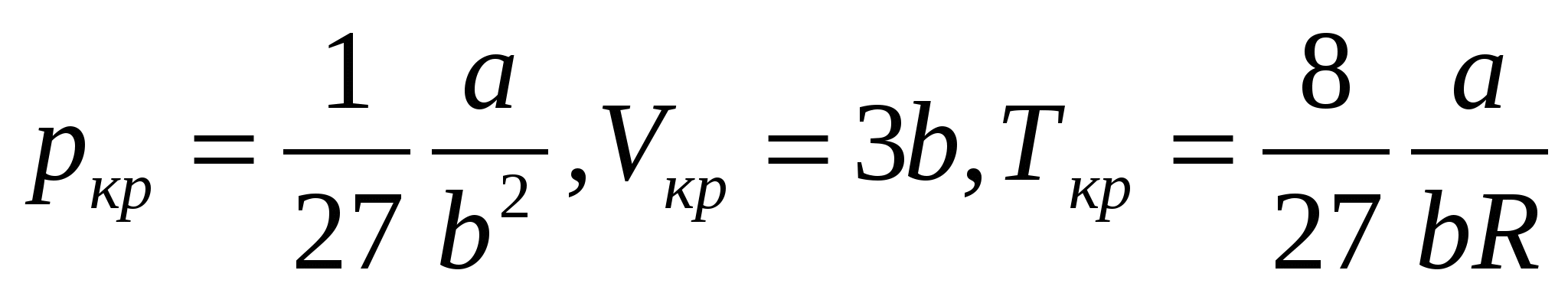
Скачать 0.72 Mb.
