Закон кулона и область его применения. Электростатика раздел, изучающий статические (неподвижные) заряды и связанные с ними электрические поля
 Скачать 1.66 Mb.
|
20)Сила Ампера :Как нам уже известно, магнитное поле оказывает на рамку с током ориентирующее действие. Значит, вращающий момент, который испытывает рамка, является результатом действия сил на отдельные ее элементы. Сравнивая и обобщая результаты исследования действия магнитного поля на различные проводники с током, Ампер открыл, что сила dF, с которой магнитное поле действует на элемент проводника dl с током, который находится в магнитном поле, равна  (1) где dl - вектор, по модулю равный dl и совпадающий по направлению с током, В - вектор магнитной индукции. Направление вектора dF может быть определено, используя (1), по правилу векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, которая действует на ток Модуль силы Ампера (см. (1)) равен  (2) где α — угол между векторами dl и В. 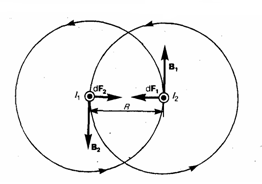 Закон Ампера используется при нахождении силы взаимодействия двух токов. Рассмотрим два бесконечных прямолинейных параллельных тока I1 и I2; (направления токов даны на рис. 1), расстояние между которыми R. Каждый из проводников создает вокруг себя магнитное поле, которое действует по закону Ампера на соседний проводник с током. Найдем, с какой силой действует магнитное поле тока I1 на элемент dl второго проводника с током I2. Магнитное поле тока I1 есть линии магнитной индукции, представляющие собой концентрические окружности. Направление вектора B1 задается правилом правого винта, его модуль по формуле (5) есть  Направление силы dF1, с которой поле B1 действует на участок dl второго тока, находится по правилу левой руки и указано на рисунке. Модуль силы, используя (2), с учетом того, что угол α между элементами тока I2 и вектором B1 прямой, будет равен  подставляя значение для В1, найдем  (3) Аналогично рассуждая, можно показать, что сила dF2 с которой магнитное поле тока I2 действует на элемент dl первого проводника с током I1, направлена в противоположную сторону и по модулю равна  (4) Сопоставление выражений (3) и (4) дает, что  т. е. два параллельных тока одинакового направления притягиваются друг к другу с силой, равной  (5) Если токи имеют противоположные направления, то, используя правило левой руки, определим, что между ними действует сила отталкивания, определяемая выражением (5). 20) Уравнения Максвелла в системе уравнений магнитостатики и электростатикиТак как на практике почти всегда приходится решать уравнения Максвелла (1) – (4) в кусочно-непрерывных средах, то граничные условия (24) следует рассматривать как неотъёмлемую часть уравнений Максвелла (1) – (4). В случае стационарных электрических и магнитных полей (  и ) система уравнений Максвелла (1) – (4) распадается на систему уравнений электростатики:  ,  ,  (25)и уравнений магнитостатики:  ,  ,  , (26)а граничные условия остаются те же |