Закон кулона и область его применения. Электростатика раздел, изучающий статические (неподвижные) заряды и связанные с ними электрические поля

• Название: Закон кулона и область его применения. Электростатика раздел, изучающий статические (неподвижные) заряды и связанные с ними электрические поля
• Анкор: Fizika_Otvety.docx
• Дата: 07.02.2018
• Размер: 1.66 Mb.
• Имя файла: Fizika_Otvety.docx
• Тип: Закон; #15311
• страница: 11 из 29

18)Закон Био-Савара-Лапласа.

Определяет величину модуля вектора магнитной индукции в точке выбранной произвольно находящейся в магнитном поле. Поле при этом создано постоянным током на некотором участке.

Закон Био-Савара-Лапласа для проводника с током I, элемент dl которого создает в некоторой точке индукцию поля dB, равен

(1)

где dl - вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, r - радиус-вектор, который проведен из элемента dl проводника в точку А поля, r - модуль радиуса-вектора r. Направление dB перпендикулярно dl и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с направлением касательной к линии магнитной индукции. Это направление может быть найдено по правилу правого винта: направление вращения головки винта дает направление dB, если поступательное движение винта совпадает с направлением тока в элементе.

Модуль вектора dB задается выражением

(2)

где α — угол между векторами dl и r.

Магнитное поле кругового тока

Определим индукцию поля в центре О кругового тока по формуле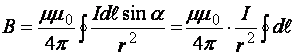

.

 

Так как , а  и  – постоянные; , так как сумма всех элементарных отрезков  составляет длину окружности.

Следовательно,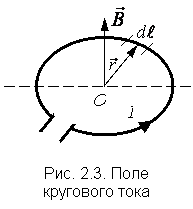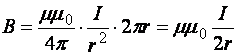

 
Магнитное поле проводника конечной длины с током.

Рассчитаем индукцию магнитного поля В, создаваемую в точке А (рис. 2.2) на расстоянии r₀ от прямолинейного проводника с током: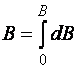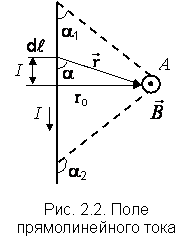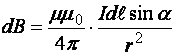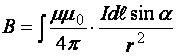

 



 

 

;

 

;

 

.                 (2.4)

 

 

Выразим переменные  и . Из рис. 2.2 видно, что . Дифференцируя это выражение, получаем: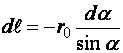

 

.

 

Из рис. 2.2 так же следует, что

 

.

 

Подставляя значения  и r в уравнение (2.4), имеем: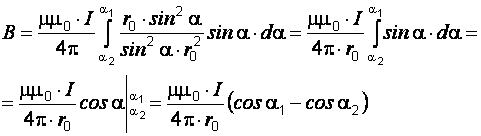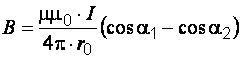

 



 

.

19)Сила Лоренца

Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца в честь великого голландского физика Х. Лоренца (1853 — 1928) — основателя электронной теории строения вещества. Силу Лоренца можно найти с помощью закона Ампера.
Рассмотрим отрезок тонкого прямого проводника с током. Пусть длина отрезка Δl и площадь поперечного сечения проводника S настолько малы, что вектор индукции магнитного поля можно считать одинаковым в пределах этого отрезка проводника. Сила тока I в проводнике связана с зарядом частиц q, концентрацией заряженных частиц n (числом зарядов в единице объема) и скоростью их упорядоченного движения v следующей формулой:

I = qnvS ( 2 )

Модуль силы, действующей со стороны магнитного поля на выбранный элемент тока, равен:

F = | I |B Δl sin α

Подставляя в эту формулу выражение ( 2 ) для силы тока, получаем:

F = | q | nvS Δl B sin α = v | q | NB sin α,


где N = nSΔl — произведение равное числу носителей тока, содержащихся в элементе тока dl. Разделив dF на это число, найдем силу F ,действующую на заряд q движущийся со скоростью v.



Сила Лоренца перпендикулярна векторам магнитной индукции и скорости упорядоченного движения заряженных частиц. Ее направление определяется с помощью того же правила левой руки, что и направление силы Ампера.
Движение частиц в однородном магнитном поле :

Для вывода общих закономерностей будем полагать, что магнитное поле однородно и на частицы не действуют электрические поля. Если заряженная частица в магнитном поле движется со скоростью v вдоль линий магнитной индукции, то угол α между векторами v и В равен 0 или π. Тогда сила Лоренца равна нулю, т. е. магнитное поле на частицу не действует и она движется равномерно и прямолинейно.

1)В случае, если заряженная частица движется в магнитном поле со скоростью v, которая перпендикулярна вектору В, то сила Лоренца F=Q[vB] постоянна по модулю и перпендикулярна к траектории частицы. По второму закону Ньютона, сила Лоренца создает центростремительное ускорение. Значит, что частица будет двигаться по окружности, радиус r которой находится из условия QvB=mv²/r , следовательно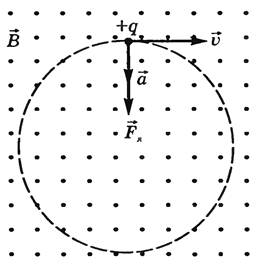

(1)



Период вращения частицы, т. е. время Т, за которое она совершает один полный оборот,



Подставив (1), получим

(2)

т. е. период вращения частицы в однородном магнитном поле задается только величиной, которая обратна удельному заряду (Q/m) частицы, и магнитной индукцией поля, но при этом не зависит от ее скорости (при v<
2)В случае, если скорость v заряженной частицы направлена под углом α к вектору В ,то ее движение можно задать в виде суперпозиции: 1) прямолинейного равномерного движения вдоль поля со скоростью v_parall=vcosα ; 2) равномерного движения со скоростью v_perpend=vsinα по окружности в плоскости, которая перпендикулярна полю. Радиус окружности задается формулой (1) (в этом случае надо вместо v подставить v_perpend=vsinα). В результате сложения двух данных движений возникает движение по спирали, ось которой параллельна магнитному полю (рис. 1). Шаг винтовой (спиральной) линии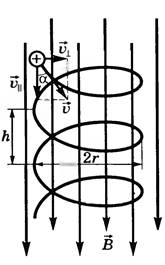



Подставив в данное выражение (2), найдем


Направление, в котором закручивается спираль, определяется знаком заряда частицы.
Если скорость v заряженной частицы составляет угол α с направлением вектора В неоднородного магнитного поля, у которого индукция возрастает в направлении движения частицы, то r и h уменьшаются с увеличением В. На этом основана фокусировка заряженных частиц в магнитном поле.