Закон кулона и область его применения. Электростатика раздел, изучающий статические (неподвижные) заряды и связанные с ними электрические поля
 Скачать 1.66 Mb.
|
21) Магнитное поле в веществе.До сих пор рассматривалось магнитное поле, которое создавалось проводниками с током или движущимися электрическими зарядами, находящимися в вакууме. Если же магнитное поле создается не в вакууме, а в какой-то другой среде, то магнитное поле изменяется. Это объясняется тем, что различные вещества, помещенные в магнитное поле, намагничиваются и сами становятся источниками магнитного поля. Вещества, способные намагничиваться в магнитном поле, называются магнетиками. Намагниченное вещество создает магнитное поле с индукцией , которое накладывается на магнитное поле с индукцией , обусловленное токами. Оба поля в сумме дают результирующее поле, магнитная индукция которого равна . Под действием поля магнитные моменты молекул приобретают преимущественную ориентацию в одном направлении, вследствие чего магнетик намагничивается – его суммарный магнитный момент становится отличным от нуля. Магнитные поля отдельных молекулярных токов в этом случае уже не компенсируют друг друга и возникает поле В'. Намагничение магнетика естественно характеризовать магнитным моментом единицы объема. Эту величину называют вектором намагничивания и обозначают J. Если магнетик намагничен неоднородно, вектор намагничения в данной точке определяется следующим выражением: 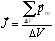 (43.2)где ΔV–физически бесконечно малый объем, взятый в окрестности рассматриваемой точки, рm – магнитный момент отдельной молекулы. Суммирование производится по всем молекулам, заключенным в объеме ΔV. Магнитный момент тока это произведение площади контура, в котором он протекает на силу тока в нем. Магнитный момент направлен перпендикулярно плоскости контура. Это направление можно определить с помощью правила буравчика. Если буравчик вращать по направлению движения тока в контуре, то его поступательное движение укажет направление магнитного момента. В случае плоского контура с электрическим током магнитный момент вычисляется как , где — сила тока в контуре, — площадь контура, — единичный вектор нормали к плоскости контура. Направление магнитного момента обычно находится по правилу буравчика: если вращать ручку буравчика в направлении тока, то направление магнитного момента будет совпадать с направлением поступательного движения буравчика. 22) Напряженность магнитного поляОна необходима для определения магнитной индукции поля, создаваемого токами различной конфигурации в различных средах. Напряженность магнитного поля характеризует магнитное поле в вакууме. Напряженность магнитного поля (формула) векторная физическая величина, равная: 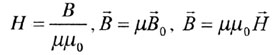 Где u0- магнитная постоянная.  Гн/м  Н/А².Напряженность магнитного поля в СИ - ампер на метр (А/м). Векторы индукции (В) и напряженности магнитного поля (Н) совпадают по направлению. Если знать Напряженность магнитного поля в данной точке, то можно определить индукцию поля в этой точке. Напряженность магнитного поля зависит только от силы тока, протекающего по проводнику, и его геометрии. С помощью следующей формулы, мы можем сформулировать теорему о циркуляции вектора H : циркуляция вектора напряженности магнитного поля по некоторому контуру равна алгебраической сумме макроскопических токов, охватываемых этим контуром.   Напряженность магнитного поля является аналогом электрического смещения. 23)Условия для H и B на границе раздела двух изотропных магнетиков : Рассмотрим поведение линий векторов магнитной индукции и напряжённости магнитного поля при переходе через границу раздела двух магнетиков. Представим себе две однородные, изотропные полубесконечные среды с магнитными проницаемостями  и  , имеющие плоскую горизонтальную границу раздела. Пусть оба магнетика находятся в однородном внешнем магнитном поле. Чтобы понять, как происходит преломление линий векторов магнитной индукции  и напряжённости магнитного поля  через эту границу, рассмотрим проекции этих векторов на саму границу и на направление, перпендикулярное границе и назовём их касательными и нормальными составляющими, соответственно.Пусть  и  ─ нормальные составляющие векторов магнитной индукции и напряжённости магнитного поля, а  и  ─ касательные составляющие тех же векторов в верхней среде, имеющей магнитную проницаемость  . Аналогичные величины в нижней среде, имеющей магнитную проницаемость  , обозначим     .Представим себе, что линии вектора преломляются при переходе через границу раздела так, как показано на рис. 1. Рассмотрим при этом преломление пока только одной силовой линии.Поместим на границе раздела воображаемую цилиндрическую поверхность с высотой h значительно меньшей радиусов оснований S1 и S2, лежащих по обе стороны от границы раздела и параллельных ей. На рисунке также показана нормаль 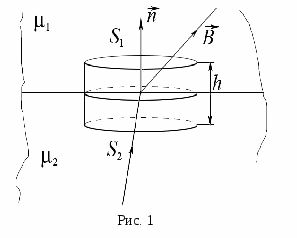 к границе раздела и к обоим основаниям. Запишем теорему Гаусса для магнитной индукции:  или  ,где S ─ замкнутая поверхность, состоящая из боковой поверхности и оснований цилиндра. Этот круговой интеграл можно разбить на 3 интеграла, каждый из которых равен потоку через верхнее и нижнее основания и боковую поверхность  .Здесь  и  ─ нормальные составляющие векторов магнитной индукции в верхнем и нижнем магнетиках, соответственно,  ─ среднее значение проекции вектора магнитной индукции на нормаль к боковой поверхности.Поскольку оба магнетика помещены в однородное внешнее магнитное поле, то все интегралы можно заменить соответствующими произведениями:  .Как и в предыдущей формуле, здесь первая составляющая магнитного потока  положительна, так как силовые линии выходят из поверхности  , а вторая составляющая  ─ отрицательна, так как силовые линии входят в поверхность  (вектора  и  спроектированы на одну и ту же нормаль). Третьей составляющей ─  можно пренебречь, так как высота цилиндра выбрана очень малой по сравнению с радиусами оснований, т. е., если  , то  .Учитывая, что  , получим: . (1)Используя связь магнитной индукции и напряжённости магнитного поля  , (2)и, применяя её для первого и второго магнетиков в формуле (1), получим:  .Отсюда следует  . (3) |