Закон кулона и область его применения. Электростатика раздел, изучающий статические (неподвижные) заряды и связанные с ними электрические поля
 Скачать 1.66 Mb. Скачать 1.66 Mb.
|
29)Нестационарные явления в теории электромагнетизма :Как известно, электрические токи порождают вокруг себя магнитное поле. Связь магнитного поля с током дала толчок к многочисленным попыткам возбудить ток в контуре с помощью магнитного поля. Эта фундаментальное открытие было блестяще сделано в 1831 г. английским физиком М. Фарадеем, который открыл явление электромагнитной индукции. Оно говорит о том, что в замкнутом проводящем контуре при изменении потока магнитной индукции, охватываемого этим контуром, возникает электрический ток, получивший название индукционного. Исследуя результаты своих многочисленных опытов, Фарадей открыл количественный закон электромагнитной индукции. Он показал, что всякий раз, когда в опыте осуществляется изменение сцепленного с контуром потока магнитной индукции, в контуре возникает индукционный ток; возникновение индукционного тока указывает на существование в цепи электродвижущей силы, которая называется электродвижущей силой электромагнитной индукции. Количественное значение индукционного тока, а значит, и э.д.с. электромагнитной индукции ξi задается только скоростью изменения магнитного потока, т. е. На следующем шаге необходимо выяснить знак ξi . Знак магнитного потока задается выбором положительной нормали к контуру, а положительное направление нормали определяется правилом правого винта. Значит, выбирая положительное направление нормали, мы знаем как знак потока магнитной индукции, так и направление тока и э.д.с. в контуре. Пользуясь этими соображениями и выводами, можно прийти к формулировке закона электромагнитной индукции Фарадея: ЭДС прямо пропорциональна скорости изменения потока электромагнитной индукции. Знак минус говорит о том, что увеличение потока (dФ/dt>0) вызывает э.д.с. ξi<0 т. е. направление поля индукционного тока навстречу потоку; уменьшение потока (dФ/dt<0) вызывает ξi>0 т.е. направления поля индукционного тока и потока совпадают. Знак минус в (2) задается правилом Ленца - общим правилом для нахождения направления индукционного тока, полученного в 1833 г. Правило Ленца: индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшему этот индукционный ток. 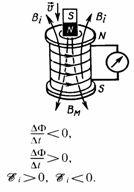 30)Самоиндукция. Взаимная индукция. Индуктивность.Электрический ток, который течет в замкнутом контуре, создает вокруг себя магнитное поле, индукция которого, согласно закону Био-Савара-Лапласа, пропорциональна току. Сцепленный с контуром магнитный поток Ф поэтому прямо пропорционален току I в контуре: где коэффициент пропорциональности L называется индуктивностью контура. Индуктивность. Способность различных проводников (катушек) индуцировать. Э. д. с. самоиндукции оценивается индуктивностью L. Она показывает, какая э. д. с. самоиндукции возникает в данном проводнике (катушке) при изменении тока на 1 А в течение 1 с При изменении в контуре силы тока будет также изменяться и сцепленный с ним магнитный поток; значит, в контуре будет индуцироваться э.д.с. Возникновение э.д.с. индукции в проводящем контуре при изменении в нем силы тока называется самоиндукцией. Из выражения (1) задается единица индуктивности генри (Гн): 1 Гн — индуктивность контура, магнитный поток самоиндукции которого при токе в 1 А равен 1 Вб: 1 Гн = 1 Вб/с = 1 В•c/А . Вычислим индуктивность бесконечно длинного соленоида. Полный магнитный поток сквозь соленоид (потокосцепление) равен μ0μ(N2I/l)S . Подставив в (1), найдем т. е. индуктивность соленоида зависит от длины l солениода, числа его витков N, его , площади S и магнитной проницаемости μ вещества, из которого изготовлен сердечник соленоида. Доказано, что индуктивность контура зависит в общем случае только от геометрической формы контура, его размеров и магнитной проницаемости среды, в которой он расположен, и можно провести аналог индуктивности контура с электрической емкостью уединенного проводника, которая также зависит только от формы проводника, его размеров и диэлектрической проницаемости среды. Найдем, применяя к явлению самоиндукции закон Фарадея, что э.д.с. самоиндукции равна Если контур не претерпевает деформаций и магнитная проницаемость среды остается неизменной (в дальнейшем будет показано, что последнее условие выполняется не всегда), то L = const и где знак минус, определяемый правилом Ленца, говорит о том, что наличие индуктивности в контуре приводит к замедлению изменения тока в нем. Если ток со временем увеличивается, то (dI/dt<0) и ξs>0 т. е. ток самоиндукции направлен навстречу току, обусловленному внешним источником, и замедляет его увеличение. Если ток со временем уменьшается, то (dI/dt>0) и ξs<0 т. е. индукционный ток имеет такое же направление, как и уменьшающийся ток в контуре, и замедляет его уменьшение. Значит, контур, обладая определенной индуктивностью, имеет электрическую инертность, заключающуюся в том, что любое изменение тока уменьшается тем сильнее, чем больше индуктивность контура. |
