ответы на билеты по физике!!!. Закон Кулона Точечным зарядом называется заряженное тело, размером которого можно пренебречь по сравнению с расстоянием от этого тела до других тел, несущих электрические заряды
 Скачать 0.88 Mb.
|
|
1.1. Закон Кулона Точечным зарядом называется заряженное тело, размером которого можно пренебречь по сравнению с расстоянием от этого тела до других тел, несущих электрические заряды.      т.е. сила взаимодействия двух точечных зарядов пропорциональ- на величине зарядов и обратно пропорциональна квадрату рас- стояния между ними. 1.2. Напряженность электрического поля Напряженость электрического поля равна силе, действующей на единичный положительный заряд, находящийся в данной точке поля. Для точечного заряда в вакууме: 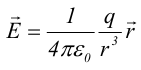 1.3. Принцип суперпозиции Напряженность электрического поля системы зарядов равна векторной сумме напряженностей полей, которые создавал бы каждый из зарядов системы в отдельности. 1.4. Теорема Гаусса для электрического поля в вакууме и ее применение к расчету полей заряженной плоскости, цилиндра, шара Поток сквозь замкнутую поверхность: 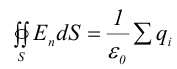  Поле бесконечной заряженной плоскости с поверхностной плотностью заряда σ=const. Е 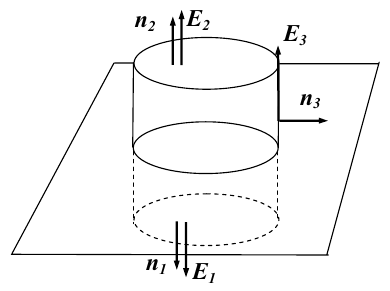 сли S−площадь основания, то поток вектора Е через оба основания будет 2ЕS. Поток через боковую поверхность цилиндра равен нулю. Следовательно, поток через всю поверхность цилиндра будет равен  . Согласно теореме Гаусса тот же поток можно представить в виде  . Сравнивая оба выражения,п  олучаемПоле тонкой бесконечно длинной прямой нити, несущей заряд с линейной плотностью λ. Т 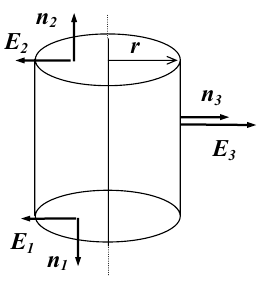 .к. вектора n1, E1 и n2, E2 взаимно перпендикулярны, то, очевидно, должны выполняться следующие равенства  Но заряд, заключенный внутри поверхности S, очевидно, равен λh. Откуда  Поле шара радиуса R, равномерно заряженного по объему с объемной плотностью заряда ρ. Поток вектора Е через эту поверхность  по теореме Гаусса равен  . Поэтому при r≥R получаем Совершенно так же вычисляется поле внутри шара. Оно определяется выражением  2.1. Потенциал электрического поля 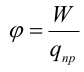 Потенциал численно равен работе, совершаемой силами поля по удалению единичного положительного заряда из данной точки в ту, где потенциал принят равным нулю.2.2. Связь напряженности и потенциала  Для точечной частицы с зарядом q 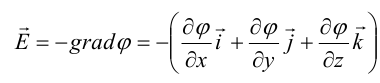   2.3. Потенциал точечного заряда, заряженной тонкостенной сферы, однородно заряженного шара. Потенциал поля точечного заряда  3.1. Электрическое поле в веществе 3.2. Полярные и неполярные молекулы Электрическим диполем называется система двух одинаковых по величине разноименных точечных зарядов +q и −q, расстояние между которыми много меньше расстояния до тех точек, в которых определяется поле системы. Различают следующие виды диэлектриков − полярные, неполярные и ионные кристаллы. Неполярные диэлектрики (Н2, О2, N2 и др,) состоят из неполярных молекул. У таких молекул “цент тяжести” положительного и отрицательного зарядов совпадают друг с другом и их дипольный момент равен нулю. Полярные диэлектрики состоят из полярных молекул (HCl,NH, H2O и др.). “Центры тяжести” положительного и отрицательного зарядов таких молекул не совпадают и их дипольный момент отличен от нуля. Кристаллическую решетку ионных кристаллов можно представить как совокупность двух подрешеток, одна из которых образована положительными ионами, другая − отрицательными. 3.3. Электронная и ориентационная поляризация Под воздействием внешнего электрического поля (если оно не очень велико) происходит процесс поляризации диэлектриков. В зависимости от типа диэлектрика механизм поляризации может быть следующим. 1. В неполярных молекулах центры тяжести положительного и отрицательного зарядов смещаются друг относительно друга и молекула приобретает дипольный момент, ориентированный вдоль вектора Е внешнего поля (электронная поляризация). 2. Полярные молекулы преимущественно ориентируют свои собственные дипольные моменты по направлению поля (ориентационная поляризация). 3. В ионных кристаллах обе подрешетки сдвигаются друг относительно друга, что также приводит к поляризации диэлектрика. 3.4. Вектор поляризации (поляризованность) Процесс поляризации диэлектрика количественно описывается с помощью вектора поляризации Р − дипольного момента единицы объема диэлектрика. 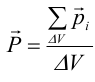 где  − дипольный момент молекул, заключенных в физическималом объеме ΔV. У изотропных диэлектриков любого типа вектор Р связан с напряженностью электрического поля в той же точке пространства (при условии, что напряженность внешнего поля много меньше напряженности внутриатомных полей) соотношением  где κ − диэлектрическая восприимчивость,− постоянная, зависящая от свойств данного вещества. 3.5. Диэлектрическая проницаемость среды Постоянная 1+κ=ε называется относительной диэлектрической проницаемостью вещества. 3.6. Вектор электрической индукции (электрическое смещение)  Для изотропных диэлектриков должно выполняться соотношение  Объемная плотность заряда - ρ. Под ρ мы понимаем плотность свобод- ных зарядов. Единственным источников вектора электрического смещения являются свободные заряды. 4.1. Теорема Гаусса для электрического поля в веществе Для поля точечного заряда q в веществе  Следовательно  где  − сумма свободных зарядов, заключенных внутри поверхности S.4.2. Условия на границе раздела двух диэлектрических сред (вывод). Рассмотрим плоскую границу двух диэлектриков, заполняющих все пространство. Пусть ε1 и ε2 − их относительные диэлектрические проницаемости. 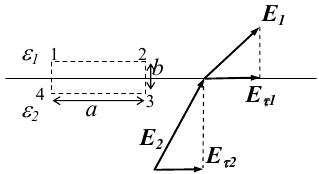 Пусть существует некое электростатическое поле. Из−за влияния связанных зарядов, возникающих на границе раздела диэлектриков, суммарное поле должно быть различным в разных веществах.Найдем циркуляцию вектора Е по прямоугольному контуру 1−2−3−4  Расстояние а считаем настолько малым, что в его пределах составляющие Еτ1 и Еτ2 можно считать постоянными. Устремляя расстояние b к нулю, получаем Еτ1=Еτ2.  Для век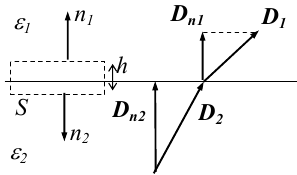тора электростатической индукции D при этом имеем , откуда  Теперь возьмем на границе диэлектриков воображаемую поверхность в виде цилиндра с площадью оснований S и высотой h (образую щая цилиндра перпендикулярна границе раздела диэлектриков). Считаем, что S настолько мало, что в пределах этой поверхности поле можно считать однородным. Поток вектора D через такую поверхность равен нулю, т.к. внутри нее нет свободных зарядов. С другой стороны этот поток можно представить как  где Sбок − площадь боковой поверхности цилиндра, а При h→0 имеем S→0, откуда Dn1=Dn2. Для напряженности электрического поля имеем 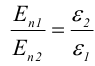 , 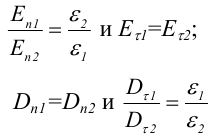 откуда  Итак, при переходе через границу двух диэлектриков, тангенциальная составляющая вектора D нормальная составляющаявектора E терпят разрыв, а нормальная составляющая D и тангенциальная составляющая Е не изменяются. При этом выполняются следующие условия:5.1. Электрическое поле внутри проводника и у его поверхности. Распределение зарядов в проводнике. В статическом случае напряженность электрического поля внутри проводника равна нулю. Если внутри проводника Е=0, то внутри проводника должны выполняться условия ϕ=const и ρ=0 (ρ − объемная плотность заряда). Таким образом, свободные заряды в проводнике могут быть распределены только на его поверхности. Напряженность электрического поля вблизи поверхности проводника направлена перпендикулярно его поверхности. 5.2. Электроемкость уединенного проводника. Во всех точках проводника потенциал имеет одно и то же значение, называемое потенциалом проводника. Потенциал проводника, естественно, зависит от величины заряда, находящегося на проводнике. Но, как показывает опыт, если параметры проводника не изменяются, то отношение заряда, которым обладает проводник, к его потенциалу остается постоянным. Электроемкостью (емкостью) проводника С называется отношение заряда q уединенного проводника к его потенциалу  5.3. Конденсаторы. Емкость конденсатора. Как уже отмечалось, уединенные проводники обладают малой емкостью. На практике же часто необходимо накапливать большие заряды при относительно малых потенциалах. Известно, что емкость проводника возрастает при приближении к нему других тел. На этом свойстве емкости построены конденсаторы. Простым конденсатором называется совокупность двух проводников (обкладок), между которыми существует электрическое напряжение и все линии смещения, исходящие из одного проводника, заканчиваются на другом. Оказывается, что разность потенциалов между обкладками конденсатора линейно зависит от величины их заряда. Под емкостью конденсатора понимают величину, пропорциональную заряду q и обратно пропорциональную разности потенциалов между обкладками U  Плоский конденсатор:  6.1. Энергия заряженного уединенного проводника и конденсатора. Потенциальная энергия взаимодействия двух точечных зарядов равна   В случае системы заряженных проводников 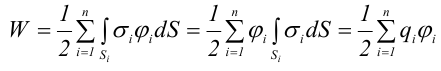 где qi − заряд, а ϕi − потенциал i−го проводника. Энергия конденсатора будет равна  6.2. Энергия электрического поля. Если известна плотность энергии электрического поля в каждой точке, то энергия, заключенная в конечном объеме V может быть вычислена по следующей формуле 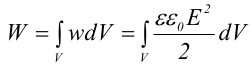 6.3. Объемная плотность энергии. Плотность энергии электрического поля, т.е. энергия, приходящаяся на единицу объема плоского конденсатора, равна 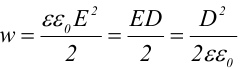 В изотропном диэлектрике направления векторов E и D совпадают, поэтому 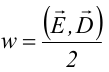 7.1. Постоянный электрический ток, его характеристики и условия существования. Электрическим током называется упорядоченное движение заряженных частиц. Для появления электрического тока необходимо осуществление следующих условий: 1. Наличие в данной среде зарядов, которые могут перемещаться на большие расстояния, т.е. свободных зарядов. Носителями тока могут быть электроны, ионы, заряженные микрочастицы. 2. Наличие в данной среде электрического поля, энергия которого затрачивается на перемещение носителей тока. Электрический ток, возникающий в проводнике вследствие того, что в нем создается электрическое поле, называется током проводимости. Для количественной характеристики электрического тока служат сила тока и плотность тока. 7.2. Разность потенциалов, электродвижущая сила, напряжение. 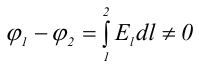 Величина, равная работе сторонних сил по переносу единичного положительного заряда по данному участку цепи называется электродвижущей силой (ЭДС), на данном участке  Падение напряжения (или просто напряжение) на данном участке цепи называется величина, численно равная работе, совершаемой электрическими и сторонними силами при перемещении по данному участку единичного положительного заряда  7.3. Закон Ома. Сила тока на однородном участке цепи пропорциональна падению напряжения на участке  здесь R − электрическое сопротивление проводника, которое зависит от его формы, размеров и свойств материала, из которого изготовлен проводник. Для однородного цилиндрического проводника  7.4. Работа, мощность и тепловое действие тока. Закон Джоуля-Ленца. Мощность, развиваемая током на этом участке  Форма выделяемой при этом энергии зависит от природы физических факторов, обуславливающих падение потенциала. Это может быть и механическая работа (электродвигатель), и магнитная энергия, и тепловая энергия. Если падение потенциала происходит на оммическом сопротивлении проводника, то вся энергия выделяется в виде тепла с мощностью  Это выражение называется закон Джоуля−Ленца. |