Закон сохранения в механие. Реферат Законы сохранения в механике. Законы сохранения в механике
 Скачать 130.95 Kb.
|
|
Реферат на тему: «Законы сохранения в механике» Выполнила: Юркова Вероника Законы сохранения энергии, импульса и момента импульса являются наиболее общими физическими законами. Они имеют глубокое происхождение, связанное с фундаментальными свойствами пространства и времени - однородностью и изотропностью. А именно: закон сохранения энергии связан с однородностью времени, закон сохранения импульса - с однородностью пространства, закон сохранения момента импульса с изотропностью пространства. Вследствие этого использование их не ограничивается рамками классической механики, они выполняются при описании всех известных явлений от космических до квантовых. Важность законов сохранения, как инструмента исследования, обусловлена следующими обстоятельствами: 1. Законы сохранения не зависят ни от траекторий частиц, ни от характера действующих сил. Поэтому они позволяют получить ряд весьма общих и существенных заключений о свойствах различных механических процессов без их детального рассмотрения с помощью уравнений движения. Если, например, выясняется, что некий анализируемый процесс противоречит законам сохранения, то можно утверждать: этот процесс невозможен, и бессмысленно пытаться его осуществить. 2. Независимость законов сохранения от характера действующих сил позволяет применять их даже в том случае, когда силы неизвестны. Так дело обстоит, например, в области микромира, где понятия материальной точки, а следовательно, и силы бессмысленны. Такая же ситуация имеет место при анализе систем большого числа частиц, когда технически невозможно определить координаты всех частиц, и поэтому - рассчитать действующие между частицами силы. Законы сохранения являются в этих случаях единственным инструментом исследования. 3. Даже в случае, если все силы известны и использование законов сохранения не дает новой по сравнению с уравнением движения (вторым законом Ньютона) информации, их применение может существенно упростить теоретические выкладки. Закон сохранения импульса. В инерциальной системе отсчета импульс замкнутой системы остается постоянным. Математически это утверждение можно выразить одним из следующих способов:  (для замкнутой) или где P - полный импульс системы материальных точек, каждая из которых обладает некоторым импульсом pi, fi - равнодействующие всех сил, приложенных к i-ой точке, Fout - сумма всех внешних сил, действующих на все материальные точки системы. При этом полагают, что и P и Fout есть векторы, приложенные к центру масс (центру инерции) системы. Закон сохранения механической энергии. В инерциальной системе отсчета полная механическая энергия замкнутой консервативной системы материальных точек остается постоянной.  (для 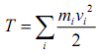замкнутой консервативной системы) или Где  - кинетическая , U - потенциальная энергии системы, δAout - работа всех внешних сил, δAin,dis - работа внутренних диссипативных сил.Закон сохранения момента импульса. В инерциальной системе отсчета момент импульса замкнутой системы материальных точек остается постоянным. ускорение энергия импульс механический  или где Mout - суммарный момент только внешних сил. Законы сохранения касаются физических систем: для отдельных составляющих этих систем они могут и не иметь места. Напомним, что: Замкнутой называется механическая система, ни на одно тело которой не действуют внешние силы. Консервативной называется механическая система, в которой все внутренние силы консервативны, а внешние консервативны и стационарны. Эти понятия являются идеализациями, но искусство физика-исследователя как раз и состоит в умении увидеть причины, по которым ту или иную реальную систему можно считать замкнутой или консервативной. В качестве примера, применения таких идеализаций ниже рассматриваются системы, в которых имеет место явление удара. Работа и мощность Согласно второму закону Ньютона, непосредственным результатом действия силы на тело является ускорение. Чтобы описать результат действия силы за конечный промежуток времени, вводится понятие работы силы. Работой силы F, действующей на материальную точку массой m при перемещении последней на dR, называют физическую величину, равную скалярному произведению силы на перемещение  Единица работы [A]=1Н·1м = 1Дж - работа, совершаемая силой в 1 Н при перемещении на 1 м вдоль направления действия силы.Если на тело действует переменная сила, то для вычисления работы перемещение разбивают на малые участки  Si и находят сначала элементарную работу на каждом участке  , а затем работу за конечный промежуток времени: Графически работа определяется как площадь криволинейной трапеции, покажем это на рисунке. По оси абсцисс в выбранном масштабе откладывают модули перемещения, по оси ординат - проекции силы на вектор перемещения  , тогда площадь трапеции численно равна работе силы.Часто бывает важным знать не только работу, но и время, в течение которого совершалась данная работа. Для этого вводится еще одна величина - мощность, характеризующая быстроту совершения работы. . Т.к.  , то работу можно представить в виде  , где скалярная величина определяет работу в единицу времени и называется мощностью, α-угол между векторами силы и скорости. Мощность - это отношение работы А к интервалу времени, в течение которого она совершается:  , в СИ мощность выражается в Вт. Мощность равна 1 Вт, если работа 1 Дж совершается за 1 с. Часто используемые кратные единицы мощности:гВт (гектоватт) = 100 Вт, кВт (киловатт) = 1000 Вт МВт (мегаватт) = 1 000 000 Вт. До сих пор в технике часто применяется такая внесистемная единица мощности, как лошадиная сила, 1 л.с. прибл. равно 735 Вт. Кинетическая энергия Рассмотрим случай, когда на тело действует постоянная сила, направление которой совпадает с направлением перемещения (т.е. cosα>=1). Подставим выражение для силы F=ma и перемещения  , получим  (5). Величину  называют кинетической энергий, а выражение представляет собой теорему о кинетической энергии, т.е. A=Ek2-Ek1 . Теорема о кинетической энергии справедлива для сил любой природы, в том числе и для переменных сил. Если на тело действует несколько сил, то подразумевается работа их векторной суммы. Кинетической энергией обладают не только тела, движущиеся поступательно, но и тела, совершающие вращательное движение.Кинетическая энергия вращающегося тела равна сумме кинетических энергий его отдельных частей:  . Т.к. угловые скорости у каждой точки вращающегося твердого тела одинаковы, то  , т.е.  , где величина, стоящая в скобках, представляет собой момент инерции тела относительно оси вращения, т.е. формулу для кинетической энергии вращающегося тела можно записать в виде (7).В практике часто встречаются случаи, когда тело вращается и одновременно перемещается в плоскости, перпендикулярной оси вращения (т.е. совершает движение, которое называется плоским). Например, движение колеса автомобиля, качение цилиндра или шара по плоскости является плоским движением. Полная кинетическая энергия тела в этом случае равна сумме кинетической энергии поступательного движения и кинетической энергии вращения вокруг оси, проходящей через центр масс  где I - момент инерции тела относительно оси, проходящей через центр масс. Из теоремы о кинетической энергии следует, что работа силы определяется разностью конечного и начального значений кинетической энергии. При этом кинетическая энергия зависит только от состояния движения тела, т.е. его скорости, но не зависит от характера процесса, с помощью которого тело начало двигаться с данной скоростью. Потенциальная энергия Потенциальной энергий взаимодействующих тел называется энергия, зависящая от взаимного расположения этих тел или частей тела. Рассмотрим невесомую горизонтальную пружину жесткости k, один конец которой закреплен, а к другому прикреплено тело массой m и приложена сила F, растянувшая пружину на x0. Когда конец пружины совершит перемещение x, то возникнет упругая сила  . Второй закон Ньютона будет иметь вид , выразим F, получим:  или  . Умножим обе части последней формулы на  , после упрощения проинтегрируем полученное выражение: В данном случае в результате совершения работы изменяется не только кинетическая энергия тела, массой m, но и форма пружины, что учитывается вторым слагаемым, представляющим собой изменение потенциальной энергии (энергия деформации). Потенциальная энергия также является функцией состояния  Может быть такая ситуация, когда изменение кинетической энергии очень мало, тогда основную роль при совершении работы будет играть изменение потенциальной энергии. Рассмотрим работу, совершаемую силой тяжести. Можно показать, что работа силы тяжести, которая действует на тело, изменяющая высоту, не зависит от формы траектории, а зависит только от начальной и конечной координаты тела. Если тело перемещается по траектории  AA1, то работа равна:A1 =mgScosα = mg (h3 - h1) Если по ломаной A1KA2, то работа равна: A2 = mgS2cosα2 + mgS1cosα1 = mg (h2 - h3) +mg (h1 - h2) = mg (h3 - h1) Силы, работа которых не зависит от формы траектории, а определяется только начальным и конечным положением точки, называются консервативными. Консервативной является не только сила, действующая у поверхности Земли (то есть частный случай силы всемирного тяготения), но вообще сила тяготения  Работа этой силы определяется выражением  т.е. результат округляется значениями радиус-векторов начальной и конечной точек. Т.о. потенциальная энергия тела в поле тяжести p = mgh + const Потенциальная энергия в поле тяготения  Потенциальная энергия деформированной пружины  Если в замкнутой системе действуют только консервативные силы, то полная механическая энергия в ней сохраняется, т.е. m = Ep + Ek = const В общем случае A = Δ(Ep + Ek) = ΔEm |